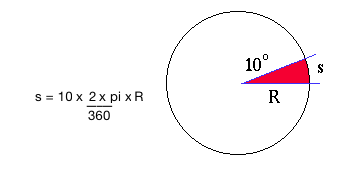
Early navagators measured distance by angular changes. For example, if a ship is at 10°N one day, then 20°N the next, it has moved 10°. The actual distance along the surface is proportional to the radius of the circle, in this case the Earth's radius, and is given by:

As navagational instruments improved, explorers were able to measure their positions to greater accuracy. But adding and subtracting angles such as 46° 33´ 12´´ from 32° 55´ 32´´ requires some manipulation. The fastest method is to convert to decimal degrees than do you arithmetic. For example, its easy to see that 25° 30´ is the same as 25.5°. Since there are 3600 arcsecs in a degree, and 60 arcmins in a degree, the formula to convert to decimal degrees looks like:
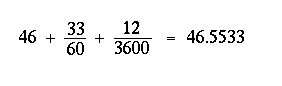
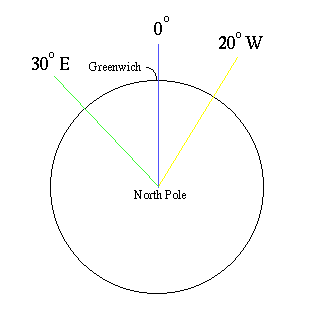
So 46° 33´ 12´´ from 32° 55´ 32´´ becomes 46.5533 - 32.9256 = 13.6278. Things are a little more complicated on the Earth's surface. We set O° at Greenwich and measure longitude as east or west of Greenwich. So for a ship at 20° W going to 30° E, the change is 50 ° not 10°.