The idea of a neutron star was developed in 1939 when calculations were made of a star that was composed solely of degenerate neutrons. If the mass of a normal star were squeezed into a small enough volume, the protons and electrons would be forced to combine to form neutrons. For example, a star of 0.7 solar masses would produce a neutron star that was only 10 km in radius. Even if this object had a surface temperature of 50,000 K, it has such as small radius that its total luminosity would be a million times fainter than the Sun.

As with white dwarfs, neutron stars have an inverse relationship between mass and radius. As a neutron increases in mass, its radius gets smaller. Their extremely small size implies that they rotate quickly, according to the conservation of angular momentum.

Angular momentum is a measure of the momentum carried by an object because of its rotation about an axis. We define an angular velocity, ω, as how fast an object turns. For example, a record turns about once every two seconds, so we say that its ω = 1/2 or 0.5 secs^-1. A car wheel turns about 100 times in a second, so we say that ω = 100. The speed of a wheel at its edge is determined by its linear speed and size such that:

where v is linear velocity and r is radius from the center of rotation. Notice that a spinning record has a constant ω. A bug near the center of the record has a small, linear velocity compared to a bug near the edge because ω is a constant, but r increases.

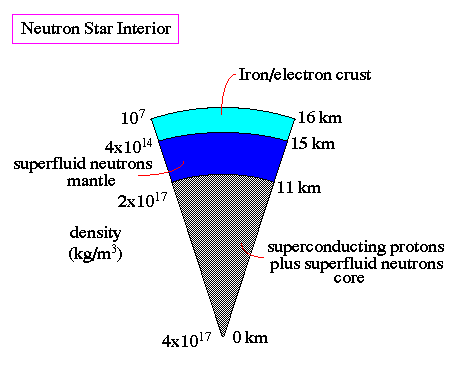
The interior of a neutron star is hard to calculate since the physics covers a new realm not testable in our laboratories. Models suggest that neutrons packed into such a dense configuration becomes a superfluid sea. Normally superfluids, such as liquid helium, occur at very low temperatures. But that normal matter has an electric charge (positive for the protons, negative for the electrons). A dense mixture of neutrons (with zero electric charge) can become a friction-free superfluid at high temperatures.

The interior of a neutron star will consist of a large core of mostly neutrons with a small number of superconducting protons. Again, normally associated with low temperatures, superconducting protons, combined with the high rotation speeds of the neutron star, produce a dynamo effect similar to what creates the Earth's magnetic field. Surrounding the core is a neutron mantle, then a iron-rich crust.

Pulsars:

Every star has a magnetic field, usually a very weak one. However, when a stellar core is compressed into a neutron star during a supernova explosion, the weak magnetic field is also compressed. As the field lines squeeze together, the magnetic field becomes very powerful. A powerful magnetic field, combined with the rapid rotation, will produce strong electric currents on the surface of the neutron star.

Loose protons and electrons near the surface of the neutron star will be sweep up and stream along the magnetic field lines towards the north and south magnetic poles of the neutron star. The magnetic axis of the neutron star does not necessarily have to be aligned with the rotation axis (like the Earth), they can be inclined from each other as shown below.

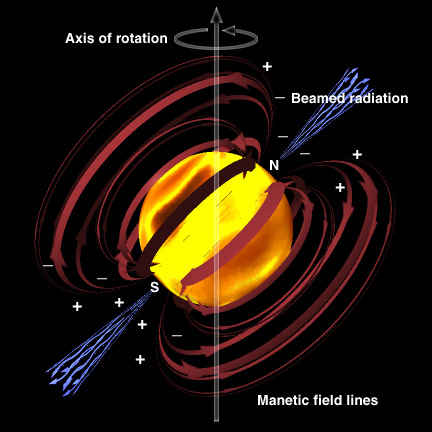
The rotating neutron star has two sources of radiation: 1) non-thermal synchrotron radiation emitted from particles trapped in the magnetic field of the neutron star, and 2) thermal radiation from particles colliding with the neutron star surface at the magnetic poles. The thermal component contains x-rays, optical and radio radiation since the protons smashing into the surface of the neutron star at extremely high velocities. Given the geometry of the hotspots at the magnetic poles, the energy from the hotspots sweeps out into space like a lighthouse. Only when the Earth lies along the axis of the neutron star is the energy detected as a series of pulses, and the object is called a pulsar.

Pulsars were discovered by accident in 1967 during a search for distant sources of radio radiation. A special telescope had been constructed to look at short timescales of radio waves. One object displayed extremely evenly spaced pulses of radiation. The period was 1.337 seconds with an accuracy of 1 part in 10 million. A typical pulsar signature is shown below.

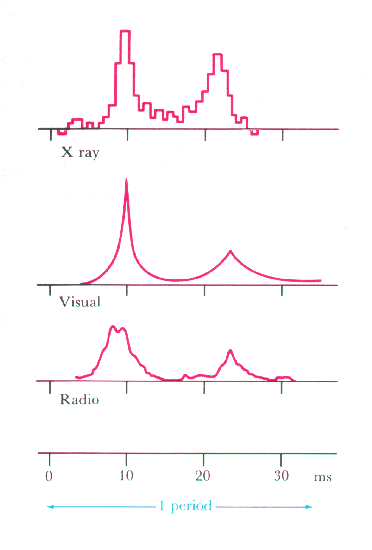
Notice that the shape of the pulses is similar from high energy photons down to the low energy radio photons. This indicates that the source of the radiation, over a range of wavelengths, is from the same region on the neutron star.

The fact that the pulses of radiation are so sharp and regular allows an astronomer to make very accurate measurements of the period of the pulses. When this is done, it is found that pulsars are slowing down with time. The rapidly changing magnetic field produces some of the energy that is beamed outward. Therefore, each pulse takes rotational energy from the neutron star and sends it into space, i.e. the neutron star loses rotational energy and slows down. Typical changes are about 10^-15 seconds per rotation. In other words, a neutron star with a rotation of 1 second will be slowed to 2 seconds in about 30 million years. Thus, the age of a pulsar is determined by its current rotation speed. Old pulsars are rotating slowly, young ones fast.

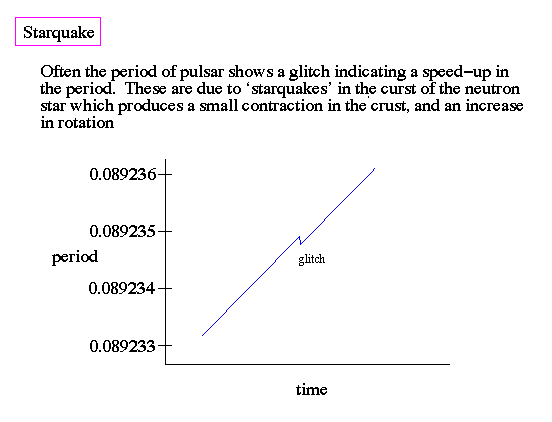
Pulsars also display sudden speed-up's in their rotation rates in sharp `glitchs' of their timing curves. The surface gravity of a neutron star is millions of times greater than the surface gravity of the Earth. The tremendous weight causes the crust to shift and contract suddenly, a starquake. The contraction, even though only a 1 mm in depth, causes a resulting starquake that is about a billion times more powerful than any earthquake on the Earth. This is visible in the rotation rate since it can be measure with a high degree of accuracy.

Accretion Disks:

If a supernova occurs in a binary system, the companion star will survive the blast (although it will lose some of its outer layers). A neutron star will be left in orbit around the secondary star. As the companion star evolves to become a red giant, its envelope will expand beyond the Roche limit and gas will spiral onto the neutron star.

The gas flowing towards the neutron star forms a thick disk of orbiting material called an accretion disk. Since the infalling gas retains the direction of orbital motion of the companion, the stream of material forms a rotating disk. Friction between the gas in neighboring orbits cause the gas to spiral inward until it hits the surface of the neutron star. As the spiraling gas moves inward, gravitational energy is released in the form of heat into the accretion disk.

The release of energy is greatest at the inner edge of the accretion disk where temperatures can reach millions of degrees. If the object at the center is very compact, then a highly energetic source is available with only a small accretion rate. This region will be the source of strong x-ray and UV radiation, the signature of an x-ray binary system such as seen in Puppisa shown below.

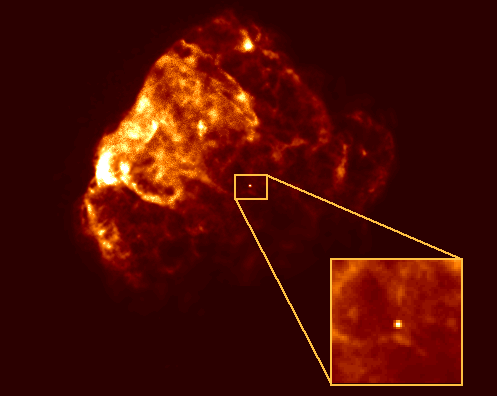
If the gas is dumped in vast amounts from the accretion disk to the neutron star, then the energy can not be released fast enough and tremendous pressures build up. The pressure can only be relieved if the gas is ejected. Since its easier for the plasmas to be ejected through the thinner poles, two powerful jets of high velocity hot gases form perpendicular to the accretion disk.

Microlensing :

When old neutrons stars have slowed down to the point where they no longer emit radio or x-ray radiation, they are invisible. However, we can detect dark neutron stars by their tremendous gravitational fields as they bend of light of stars behind them, called gravitational microlensing.

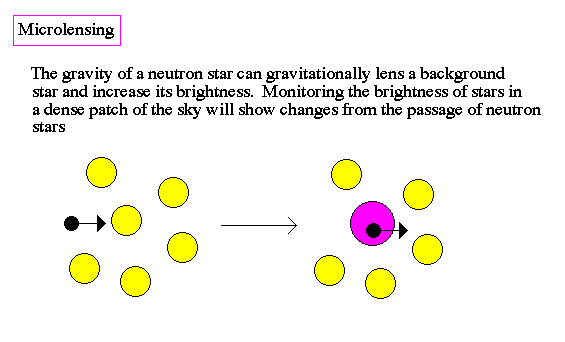
Surveys of microlensing will image a patch of the sky towards the center of the galaxy looking for sharp changes in light over a period of weeks. A computer monitors the brightesses of millions of stars looking for a variation.

These changes in brightness mark the passage of a neutron star in front of the target star, and the lensing of the background star light by the neutron star.

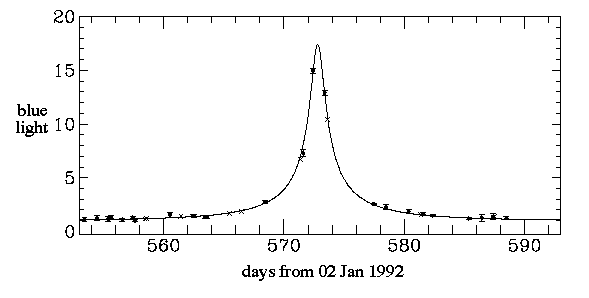
The period and shape of the microlensing event provides information on the mass of the neutron star.