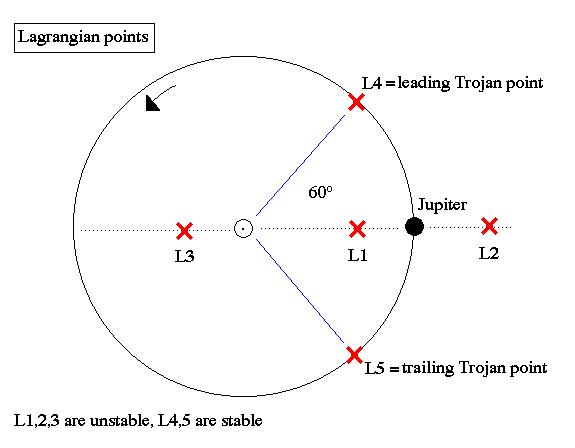
Lagrangian point is a point in space at which a small body, under the gravitational influence of two large ones, will remain approximately at rest relative to them. The existence of such points was deduced by the French mathematician and astronomer Joseph-Louis Lagrange in 1772. In 1906 the first examples were discovered: these were minor planets moving in Jupiter's orbit, under the influence of Jupiter and the Sun.

In each system of two heavy bodies (e.g., Sun-Jupiter, or Earth-Moon) there exist five theoretical Lagrangian points, but only two are stable--i.e., will tend to retain small bodies despite slight perturbations by outside gravitational influences. Each stable point forms one tip of an equilateral triangle having the two massive bodies at the other vertices.

Excerpt from the Encyclopedia Britannica without permission.