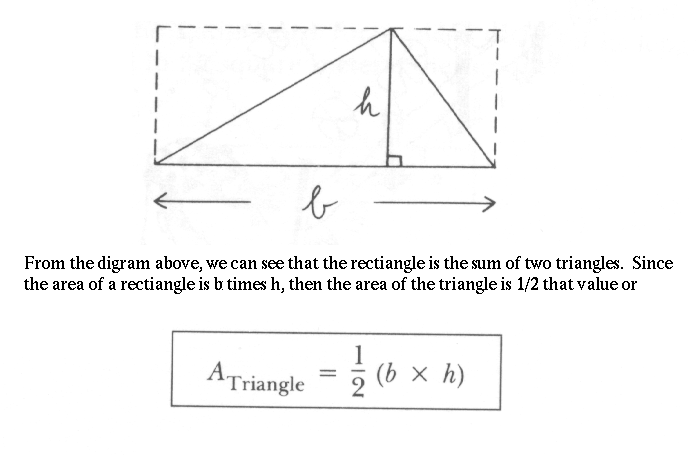Pythagoras, contorniate medallion engraved between AD 395 and 410

Pythagoras:

Pythagoras (fl. 530 BCE) must have been one of the world's greatest men, but he wrote nothing, and it is hard to say how much of the doctrine we know as Pythagorean is due to the founder of the society and how much is later development. It is also hard to say how much of what we are told about the life of Pythagoras is trustworthy; for a mass of legend gathered around his name at an early date. Sometimes he is represented as a man of science, and sometimes as a preacher of mystic doctrines, and we might be tempted to regard one or other of those characters as alone historical. The truth is that there is no need to reject either of the traditional views. The union of mathematical genius and mysticism is commonly enough. Originally from Samos, Pythagoras founded at Kroton (in southern Italy) a society which was at once a religious community and a scientific school. Such a body was bound to excite jealousy and mistrust, and we hear of many struggles. Pythagoras himself had to flee from Kroton to Metapontion, where he died.

It is stated that he was a disciple of Anaximander, his astronomy was the natural development of Anaximander's. Also, the way in which the Pythagorean geometry developed also bears witness to its descent from that of Miletos. The great problem at this date was the duplication of the square, a problem which gave rise to the theorem of the square on the hypotenuse, commonly known still as the Pythagorean proposition (Euclid, I. 47). If we were right in assuming that Thales worked with the old 3:4:5 triangle, the connection is obvious.

Pythagoras argued that there are three kinds of men, just as there are three classes of strangers who come to the Olympic Games. The lowest consists of those who come to buy and sell, and next above them are those who come to compete. Best of all are those who simply come to look on. Men may be classified accordingly as lovers of wisdom, lovers of honor, and lovers of gain. That seems to imply the doctrine of the tripartite soul, which is also attributed to the early Pythagoreans on good authority, though it is common now to ascribe it to Plato. There are, however, clear references to it before his time, and it agrees much better with the general outlook of the Pythagoreans. The comparison of human life to a gathering like the Games was often repeated in later days. Pythagoras also taught the doctrine of Rebirth or transmigration, which we may have learned from the contemporary Orphics. Xenophanes made fun of him for pretending to recognize the voice of a departed friend in the howls of a beaten dog. Empedocles seems to be referring to him when he speaks of a man who could remember what happened ten or twenty generations before. It was on this that the doctrine of Recollection, which plays so great a part in Plato, was based. The things we perceive with the senses, Plato argues, remind us of things we knew when the soul was out of the body and could perceive reality directly.

There is more difficulty about the cosmology of Pythagoras. Hardly any school ever professed such reverence for its founder's authority as the Pythagoreans. 'The Master said so' was their watchword. On the other hand, few schools have shown so much capacity for progress and for adapting themselves to new conditions. Pythagoras started from the cosmical system of Anaximenes. Aristotle tells us that the Pythagoreans represented the world as inhaling 'air' form the boundless mass outside it, and this 'air' is identified with 'the unlimited'. When, however, we come to the process by which things are developed out of the 'unlimited', we observe a great change. We hear nothing more of 'separating out' or even of rarefaction and condensation. Instead of that we have the theory that what gives form to the Unlimited is the Limit. That is the great contribution of Pythagoras to philosophy, and we must try to understand it. Now the function of the Limit is usually illustrated from the arts of music and medicine, and we have seen how important these two arts were for Pythagoreans, so it is natural to infer that the key to its meaning is to be found in them.

It may be taken as certain that Pythagoras himself discovered the numerical ratios which determine the concordant intervals of the musical scale. Similar to musical intervals, in medicine there are opposites, such as the hot and the cold, the wet and the dry, and it is the business of the physician to produce a proper 'blend' of these in the human body. In a well-known passage of Plato's Phaedo (86 b) we are told by Simmias that the Pythagoreans held the body to be strung like an instrument to a certain pitch, hot and cold, wet and dry taking the place of high and low in music. Musical tuning and health are alike means arising from the application of Limit to the Unlimited. It was natural for Pythagoras to look for something of the same kind in the world at large. Briefly stated, the doctrine of Pythagoras was that all things are numbers. In certain fundamental cases, the early Pythagoreans represented numbers and explained their properties by means of dots arranged in certain 'figures' or patterns.

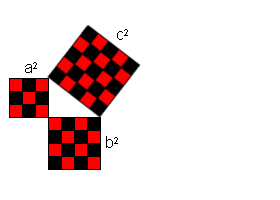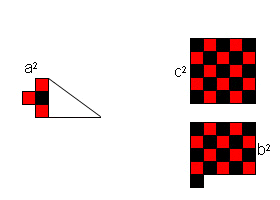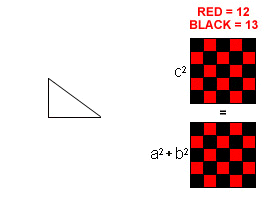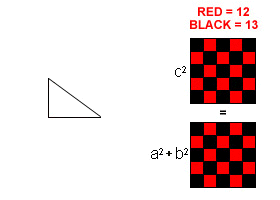
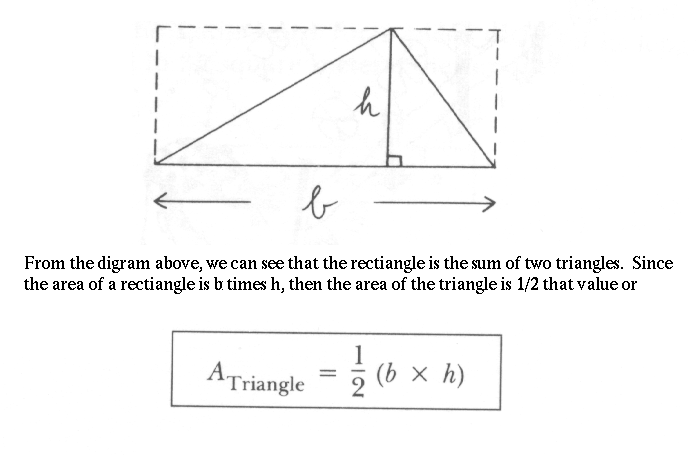
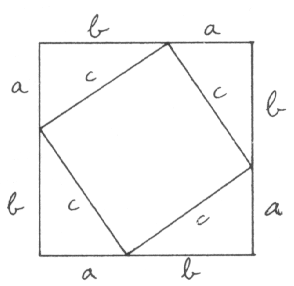
Excerpt from the Encyclopedia Britannica without permission.