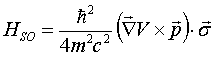Main Page Current Research Programs

Fermi Contours of Metal Surfaces and Ultrathin Films

Primary Collaborators: Eli Rotenberg, Advanced Light Source

Joerg Schaeffer, University of Oregon (now at University of Augsberg)

Boris Krenzer, University of Oregon (now at University of Essen)

Matthew Rocha, University of Oregon (now at HP Corvallis)

Oleg Krupin, University of Oregon

 

Clean and Modified Group VIB Metal Surfaces

PRL 80, 2905 (1998); PRL 82, 4066 (1999); PRL 84, 2925 (2000); PRL 89, 216802 (2002)
JVST, 19 (4), 1983 (2001); J. Elect. Spectroscopy, 117-118, 57-70 (2001); J. Elect. Spectroscopy, 126, 125 (2002)

For the past two decades, we have focused much attention on the electronic structure of clean and adsorbate-modified transition metal surfaces.  Our motivation for these studies has been to forge a connection between surface electronic structure and low energy excitations such as surface phonons and adsorbate vibrations. For example, our early studies of the surface Fermi contours on W(110) [1]and Mo(110) motivated detailed measurements of surface phonon dispersion relations. These have provided the best current example of a surface phonon anomaly,[3, 4] a result which was qualitatively though not quantitatively predicted by our Fermi contours and which has also motivated serious theoretical attention.[5-7] Given the (at best) qualitative match between our early experimental Fermi contours and recent calculated contours, and the success of the latter in predicting the location of a phonon anomaly, we were motivated to check our results to determine what went wrong.  Our new results have proven quite interesting and are indicative of interesting new physics. The primary results have been published recently.[8-12] One key result is given in Fig. 1, which shows the Fermi contours for various submonolayer coverages hydrogen atoms adsorbed onto W(110). The contours of interest are labeled 1 and 2.  The calculation (and the previous experiment) observed just one contour, while we observe a clear splitting between these two on W(110) and a barely-resolvable splitting in Mo(110).  We believe that this contour is split by the spin-orbit interaction that, due to the lack of inversion symmetry caused by the surface, breaks the Kramer's degeneracy.[13, 14] The calculations to date do not include the spin-orbit interaction and thus do not predict this sizable splitting.  The nesting vector that provides the best match to the observed phonon anomaly couples contours 1 and 2 on opposite side of the surface Brillouin zone.  The results suggest part of what went wrong previously.  The image in Fig 1 was collected in ~20 minutes.  A similar image could not have been collected 10 years ago - it would have taken longer than sample stability would allow.  Instead, the contour was pieced together one point at a time.  The much more rapid and systematic data collection algorithm enabled by the ALS allowed this new and interesting result to be obtained.

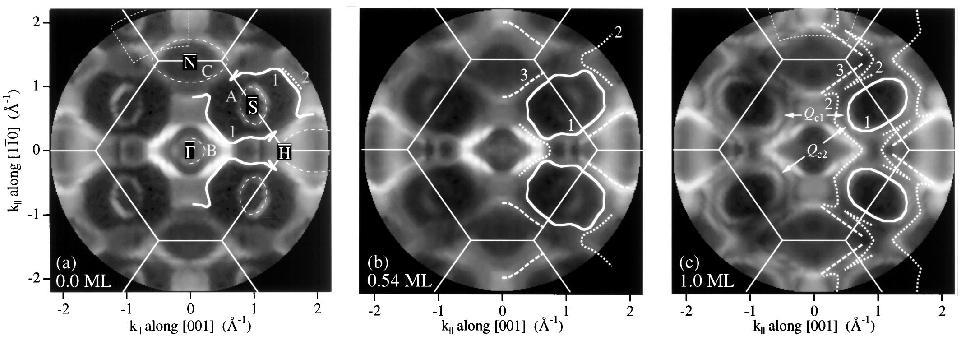
Fig. 1: Momentum-dependent Fermi level photoemission intensity for a) clean W(110), b) 0.5 ML of hydrogen adsorbed onto W(110), and c) 1 ML of hydrogen adsorbed onto W(110). Fermi contours correspond to maxima in intensity and are indicated by white lines.


The splitting of this contour is interesting in its own right.  In line with previous work by LaShell, et. al.[13] on Au(111), we have proposed the splitting of bands 1 and 2 discussed above produces an unusual spin ordering on W(110).  The spin-orbit interaction is governed by the Hamiltonian

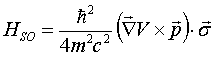
Since  is normal to the surface plane  is in the plane for a 2D surface state, the energy splitting must be primarily between in-plane polarized spins.  Fig. 2 shows the valence band ARP intensity at the Fermi level for 1 ML of Li (for which the splitting is also observed) on W(011) (Fig. 2, left) and on Mo(011) (Fig. 2, right).  The arrows show the proposed relative in-plane spin orientations, and were drawn in such a way that states at -k|| have spins flipped relative to those at +k||, as required by time-reversal symmetry. [14]   Despite these unusual spin structures, the surfaces have no net magnetic moment.  Mo(110) exhibits a Fermi contour that is insignificantly split compared to that of W(110), as expected for this lighter (though isoelectronic) metal.

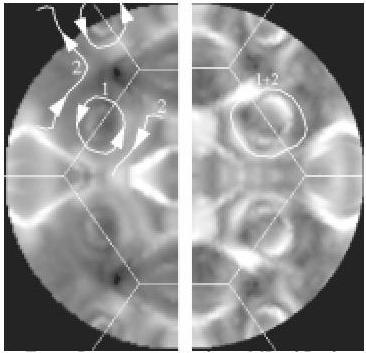
Fig. 2: Proposed Fermi-level spin orderings for saturation coverage of lithium on W(110) (left) and Mo(110) (right). The two contours labeled 1 and 2 are split by the spin-orbit interaction on W(110), but the related splitting on Mo(110) is barely resolved and is not visible in these contours.

Recently, using spin- and angle-resolved photoemission in collaboration with Michael Hochstrasser and Jim Tobin at Lawrence Livermore National Lab, we have directly observed the spin polarization of these two states for W(110)-(1x1)H. [12] The key result is shown in Fig. 3.  This shows spin-resolved spectra of the S1-S2 doublet near the Fermi energy, for both tangential and longitudinal spin components.  The tangential components clearly resolve the splitting and prove that the spin orientation is in-plane, in the orientation predicted by the spin-orbit Hamiltonian.


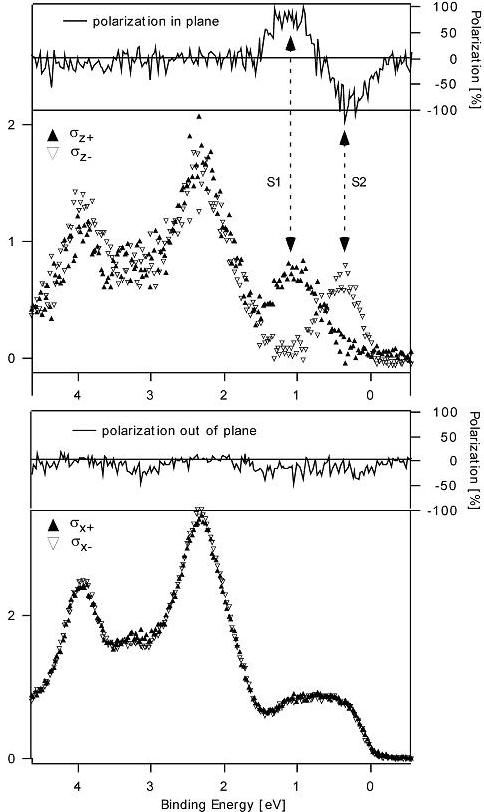
Fig. 3: Spin-resolved photoemission of the state S1 and S2, showing that they are spin-polarized in opposite direction with the spin orientation in the surface plane.

These states and their Fermi contours are interesting because they have a profound effect on the elementary excitations at these surfaces. For example, the observed spin splitting implies that spin conservation needs to be taken into consideration as part of this electron-phonon coupling process that leads to the phonon anomalies observed on these surfaces.  Moreover, there will be distinct spin excitations at these surfaces, and the dispersion relations of these will be determined by the spin ordering of these contours.  Finally, these spin orderings will very likely impact the interfacial magnetic structure between a heavy metal like tungsten and a magnetic metal.


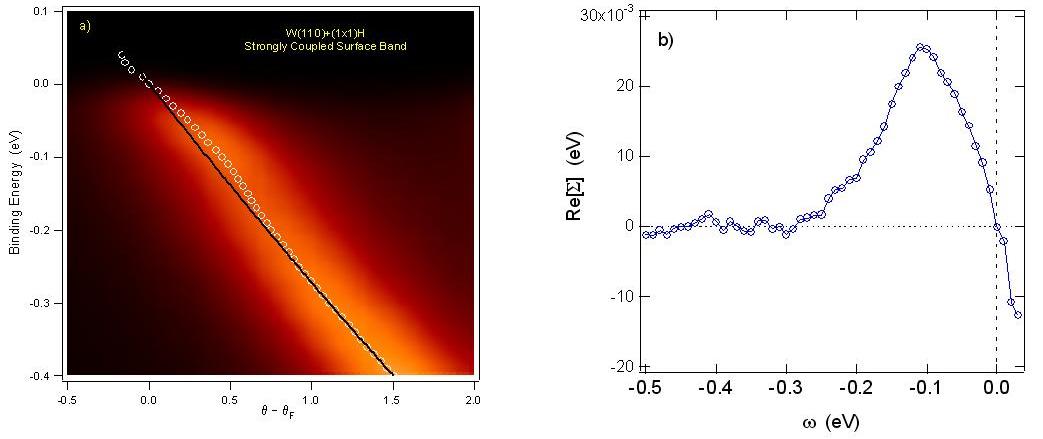
Fig. 4: High resolution band map (left) and the real part of the derived electron-phonon self-energy function for the S1 surface state on W(110)-(1x1)H.

Our crowning achievement in studying the H/W(110) system is the direct observation of coupling between these surface localized electron states with the adsorbed hydrogen vibrational modes. [10, 11]   The data in figure 1 provide a nice way to conceptualize this coupling.  If we were to start with a full monolayer coverage, and then slowly and uniformly remove hydrogen layer, the Fermi contours would slowly evolve from the right panel to the left.  Oscillating the layer rather than removing it would cause the electron gas to respond in similar fashion.  Such a conceptual motion corresponds directly to the zero-wave-vector symmetric stretch hydrogen phonon mode.  So, as the layer vibrates, it naturally couples to sizable reorganization of the electronic structure, as manifested by the Fermi contours.  To the extent that electronic motion lags the vibrational motion, such a mechanism implies a breakdown of the Born-Oppenheimer approximation.  Fig. 4 shows directly the perturbations on the underlying quasiparticle dispersion relations driven by this electron-phonon coupling.

Surface Phonon Anomalies on Mo(x)Re(1-x) Alloy Surfaces

preprint

Recently, in collaboration with Ward Plummer at the University ot Tennessee and Michio Okada at the University of Osaka, we have begun to extend this work on electron-phonon coupling to simple binary alloy surfaces. We have initiated our work with Mo-Re alloys, as these have been well-characterized by other techniques. Our motivation for moving in this direction is to study the impact of compositional disorder on material properties - subject of prime focus in many materials systems, ranging from simple metal alloys to complex oxides and compound semiconductors. The macroscopic properties of interest are driven microscopically by manybody couplings between the electron gas and various low-energy bosonic degrees of freedom. Disorder will broaden electronic and the bosonic modes to varying degrees, and in the limit of very strong damping, one or more of these modes can even become localized. The question of how the variously damped modes remain coupled is of enduring fundamental interest and also of much practical importance.

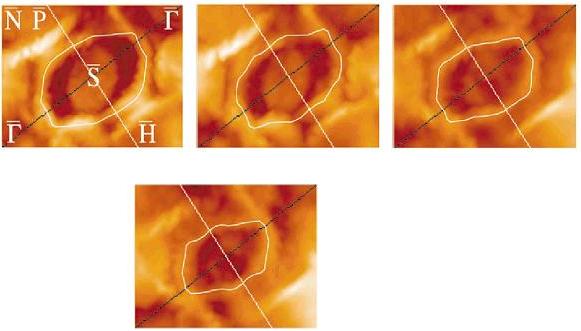
Fig. 5: Variation of the hole pocket as a function of rhenium concentration on MoRe alloy surfaces.

Figure 5 shows the evolution of the hole pocket that drives the phonon anomaly on Mo(110)[15, 16] as a function of alloy composition.  As the rhenium concentration is increased, the hole pocket decreases in size.  This is qualitatively as expected based on the rigid band model of alloys.  Rhenium has one more valence electron than the host molybdenum, and this extra electron will be donated to the host band structure, thereby raising the Fermi level.  Alloying naturally decreases the size of this hole pocket. Moreover, our results predict the evolution of the position of the phonon anomaly as the composition is changed[17] with good precision, though not the width.  We have also undertaken an accurate test of the rigid band model for this system.

Spin Density Wave Band Gap and Phase Diagram on Cr(110)

PRL 83, 2069 (1999); Surface Science 454-456, 885 (2000).

We have recently extended our measurements of Mo(110) and W(110) to the more technically challenging though somewhat more exotic Cr(110) surface. [15]   Our goal was to understand how the well-known bulk itinerant antiferromagnetism in chromium is modified near a surface. [16]   Fermi contours for the clean surface are shown below.

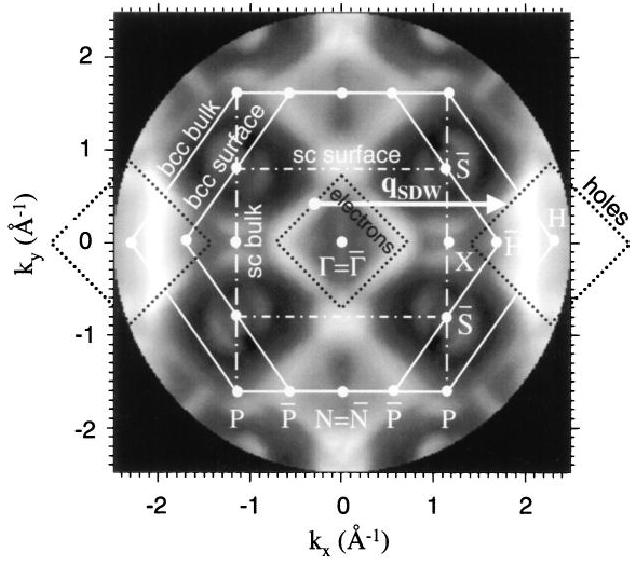
Fig. 6:  Surface BZ and bulk BZ superimposed on ARPES Fermi level intensity plot. SDW nesting occurs between the electron jack at G and the hole jack at H. The data provide an estimate for qSDW = 0.95 ± 0.05 G–H.

The derived nesting vector is close to that of the bulk.  Indeed, these are bulk states that propagate to the surface, and are thus the ones that drive the SDW state.  We have measured the SDW band gap, and have shown that it exists over much of the electron jack.  This is the first direct, momentum-resolved confirmation of an electronic driving force for SDW formation.  We have also measured the temperature dependence of the SDW band gap, and we find an enhanced surface Néel temperature.

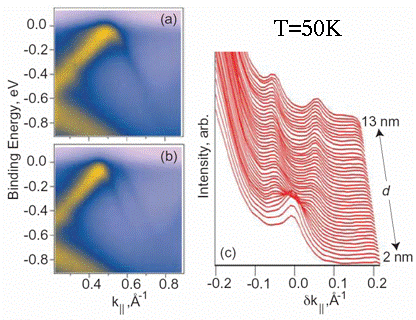
Fig. 7:  Band maps of Cr(110) films as a function of thickness in at T=50K in the vicinity of the SDW band gap and band backfolding.  The unsplit and split bands are associated with commensurate and incommensurate SDW phases, respectively.  The panel on the right shows the smooth evolution of the splitting as a function of temperature.

More recently we have used angle-resolved photoemission to probe the SDW commensurability and phase behavior of Cr(110) films.  A sampling of the relevant results is shown in Fig. 7, which provides band maps along the  direction of the surface Brillouin zone.  This line intersects the electron octahedron that helps drive the SDW ground state.  These data were collected at T = 50K, from a film with a wedge-shaped thickness profile that allows straight-forward measurements as a function of thickness.  The thinner film shows a single backfolded band that is related to a commensurate SDW state, while the thicker film shows two backfolded bands associated with an incommensurate SDW.  We have used results like to these to map the SDW commensurability and phase diagram as a function of thickness and T.

Electron states in 1D and Quasi-1D systems

PRL 87, 157 (2001); PRL 91, 066401 (2003); Surface Rev. Lett. 9, 1029 (2002).

One-dimensional (1D) solids are of great interest because of the many unusual phenomena they may exhibit, such as Peierls instabilities and deviations from Fermi liquid behavior.  Photoemission appears particularly suited to probe these exotic electronic properties.  An important topic is the effect of Peierls instabilities on the periodicity of experimentally determined electron bands.  In the simplest case of a half-filled band, a Peierls distortion leads to a new Brillouin zone of half the original width.  More generally, a charge density wave (CDW) can induce a zone that is incommensurate with the underlying lattice.  It lifts the original symmetry of the lattice and leads to a total loss of translational symmetry.  Electronic band structure, often derived from translational invariance, can still exist in systems with incommensurate periodic potentials.  One of the most intriguing compounds in this respect is NbSe3 with its two incommensurate charge density waves.  This system has been heavily studied by a variety of transport and optical techniques, yet the underlying electron states that drive the CDW states had not previously been carefully studied, largely due to the needle-like macroscopic texture of the material.


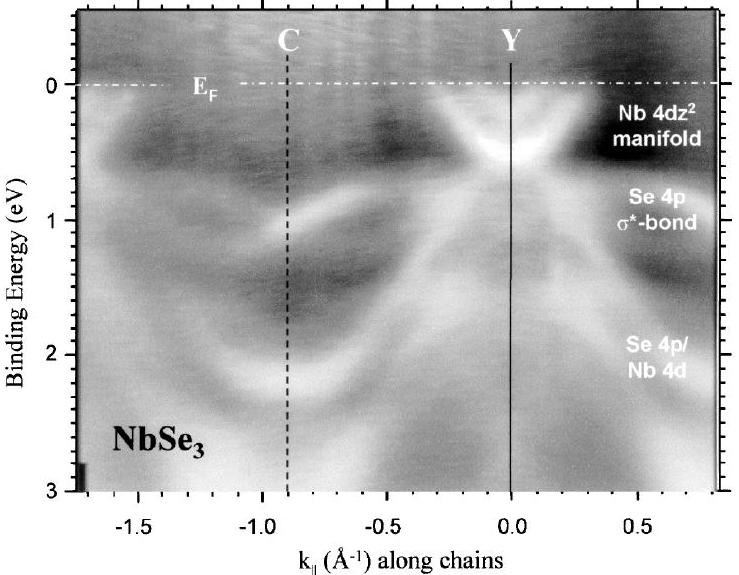
FIG. 6: Electronic band structure along the NbSe3 whiskers. Near the Fermi level two sets of parabolic bands are clearly discernible. They originate from Nb 4d states and supply the nesting conditions for the CDWs.

We have recently studied this system’s electron states with high resolution photoemission. [17]   The prime result is shown in Fig. 6 above.  This shows the electronic band structure along the direction of high dispersion for this material.  The two parabolic bands near the Fermi level (zero binding energy) provide the necessary nesting conditions that drive the CDW ground states.

 

Acknowledgement

This work was carried out in part at the Advanced Light Source at Lawrence Berkeley National Laboratory which is supported by the U.S. Department of Energy. Financial support from the USDOE under grant DE-FG06-86ER45275 is gratefully acknowledged.

 

References 

1. Gaylord, R.H., K. Jeong, and S.D. Kevan, Experimental Fermi Surface for Clean and Hydrogen-Covered W(011). Phys. Rev. Lett., 1989. 62: p. 2036.
2. Jeong, K., R.H. Gaylord, and S.D. Kevan, Experimental Fermi Surface of Mo(011). Phys. Rev. B, 1989. 39: p. 2973.
3. Hulpke, E. and J. Lüdecke, Hydrogen-Induced Phonon Anomaly on the W(110) Surface. Phys. Rev. Lett., 1992. 68(18): p. 2846-2849.
4. Balden, M., et al., Surface Phonons on the clean and H-covered W(011) surface measured with EELS. Surface Sci., 1994. 307-9: p. 1141.
5. Bungaro, C., S.d. Gironcoli, and S. Baroni, Theory of the anomalous Rayleigh dispersion at H/W(110) surfaces. Phys. Rev. Lett., 1996. 77: p. 2491.
6. Kohler, B., et al., H-Induced Instability of Mo(011). Zeitschrift f. Physikalische Chemie, 1996. 197: p. 193.
7. Kohler, B., et al., Frustrated H-Induced Instability of Mo(011). Phys. Rev. Lett., 1995. 74: p. 1387.
8. Rotenberg, E., J.W. Chung, and S.D. Kevan, Spin-orbit-coupling induced surface band splitting in Li/W(110) and Li/Mo(110). Phys. Rev. Lett., 1999. 82: p. 4066.
9. Rotenberg, E. and S.D. Kevan, Evolution of Fermi level crossings vs. H coverage on W(110). Phys. Rev. Lett., 1998. 80(13): p. 2905.
10. Rotenberg, E. and S.D. Kevan, Electron-Phonon Coupling in W(110)-(1x1)H. J. Elec. Spect., 2002. 126: p. 125.
11. Rotenberg, E., J. Schaefer, and S.D. Kevan, Coupling between Adsorbate Vibrations and an Electronic Surface State. Phys. Rev. Lett., 2000. 84: p. 2925.
12. Hochstrasser, M., et al., Spin-resolved photoemission of surface states of W(110)-(1x1)H. Phys. Rev. Lett., 2002. 89: p. 216802.
13. LaShell, S., B.A. McDougall, and E. Jensen, Spin splitting of an Au(111) surface band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett., 1996. 77(16): p. 3419-22.
14. Kittel, C., Quantum Theory of Solids. 1987, New York: Wiley.
15. Hulpke, E. and J. Lüdecke, The giant surface phonon anomaly on hydrogen saturated W(110) and Mo(110). Surface Sci., 1992. 272: p. 289.
16. Hulpke, E. and J. Lüdecke, The giant surface phonon anomaly on hydrogen saturated W(110) and Mo(110). Surface Sci., 1993. 287/288: p. 837-841.
17. Okada, M., et al., Shifting the surface Kohn anomaly of H-saturated Mo(110) by alloying the bulk with Re. Surface Sci., 2002. 498: p. L78-84.
18. Schäfer, J., et al., Direct Spectroscopic Observation of the Energy Gap Formation in the Spin Density Wave Phase Transition at the Cr(110) Surface. Phys. Rev. Lett., 1999. 83: p. 2069.
19. Fawcett, E., Spin-density-wave antiferromagnetism in chromium. Rev. Mod. Phys., 1988. 60: p. 209.
20. Schäfer, J., et al., High Temperature Symmetry Breaking in the Electronic Band Structure of the Quasi-One-Dimensional Solid NbSe3. Phys. Rev. Lett., 2001. 87(19): p. 196403.