Dynamical Tunneling in the Open Annular
Billiard
The ray picture
is not always adequate to describe resonance lifetimes in
asymmetric resonant cavities (ARCs). Important
corrections may arise due to classically forbidden tunneling
phenomena.
This can be studied in the
annular billiard, a circular resonator with a non-concentric inner
circle that cannot be penetrated. The outer circle could be a glass-air
interface, and the inner circle a metallic inclusion. In addition, we
coated
the outer surface with a thin but penetrable metallic film to increase
all resonance lifetimes. The annular billiard with impenetrable outer
walls has been studied (among others) by Doron and Frischat,
as an example for the effects of chaos on tunneling processes. The
work I
did with Gregor Hackenbroich shows that the
leaky annular
billiard
shows resonance lifetimes that fluctuate strongly with
deformation, due to
dynamical tunneling. That is a wave
correction
to the geometric-optics picture which arises only in systems for which
the
wave equation is non-separable, i.e. whose short-wavelength limit can
exhibit chaos. The
paper we wrote on
this
subject only scratches the surface of this poorly understood
phenomenon.
The reason why this is a hard problem lies in the fact that the
classical
phase space structure in itself is very complex because chaos and
regularity
coexist in these resonator billiards.
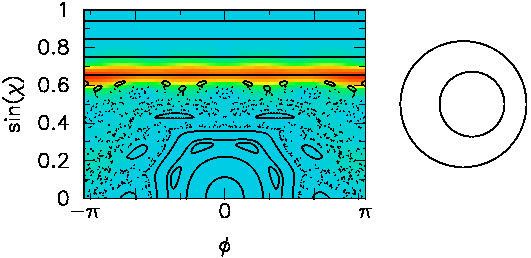 Shown on the left are the phase-space portraits of the annular billiard of
the shape
indicated on the right. The false-color plot represents a metastable
wave function in the annular region between inner and outer circle,
projected onto the phase space. This representation is called a Husimi
plot.
The highest weight in the first plot is concentrated on a region
where the classical dynamics is regular (not chaotic). For these
trajectories, it
is difficult to leak out of the resonator, so that the corresponding
lifetime is very long.
Shown on the left are the phase-space portraits of the annular billiard of
the shape
indicated on the right. The false-color plot represents a metastable
wave function in the annular region between inner and outer circle,
projected onto the phase space. This representation is called a Husimi
plot.
The highest weight in the first plot is concentrated on a region
where the classical dynamics is regular (not chaotic). For these
trajectories, it
is difficult to leak out of the resonator, so that the corresponding
lifetime is very long.
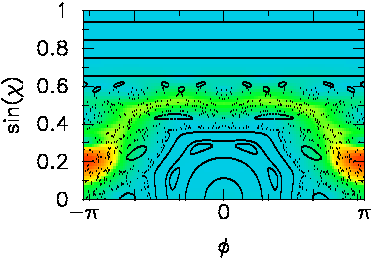 At the same deformation, but at a slightly different frequency, one
finds
a broad resonance associated with chaotic rays that can classically
diffuse
to regions in phase space where escape is easiest, namely the bottom
of
the plot. In this region, trajectories impinge on the outer boundary
with
large momentum (χ is
the angle of incidence
with respect to the normal).
At the same deformation, but at a slightly different frequency, one
finds
a broad resonance associated with chaotic rays that can classically
diffuse
to regions in phase space where escape is easiest, namely the bottom
of
the plot. In this region, trajectories impinge on the outer boundary
with
large momentum (χ is
the angle of incidence
with respect to the normal).
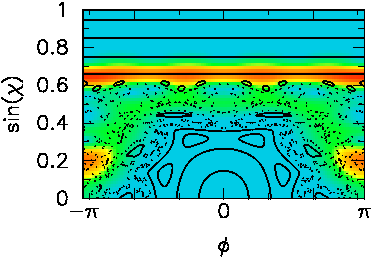 When the deformation is changed by a minute amount, the two states
above are coupled
due to their energetic overlap, and the wave function has weight on
the regular
and chaotic regions alike. This is called
dynamical tunneling because it represents a phase space distribution
that
cannot be generated by a classical trajectory.
When the deformation is changed by a minute amount, the two states
above are coupled
due to their energetic overlap, and the wave function has weight on
the regular
and chaotic regions alike. This is called
dynamical tunneling because it represents a phase space distribution
that
cannot be generated by a classical trajectory.
This page
© Copyright Jens Uwe Nöckel,
05/2001

 Shown on the left are the phase-space portraits of the annular billiard of
the shape
indicated on the right. The false-color plot represents a metastable
wave function in the annular region between inner and outer circle,
projected onto the phase space. This representation is called a Husimi
plot.
The highest weight in the first plot is concentrated on a region
where the classical dynamics is regular (not chaotic). For these
trajectories, it
is difficult to leak out of the resonator, so that the corresponding
lifetime is very long.
Shown on the left are the phase-space portraits of the annular billiard of
the shape
indicated on the right. The false-color plot represents a metastable
wave function in the annular region between inner and outer circle,
projected onto the phase space. This representation is called a Husimi
plot.
The highest weight in the first plot is concentrated on a region
where the classical dynamics is regular (not chaotic). For these
trajectories, it
is difficult to leak out of the resonator, so that the corresponding
lifetime is very long.
 At the same deformation, but at a slightly different frequency, one
finds
a broad resonance associated with chaotic rays that can classically
diffuse
to regions in phase space where escape is easiest, namely the bottom
of
the plot. In this region, trajectories impinge on the outer boundary
with
large momentum (χ is
the angle of incidence
with respect to the normal).
At the same deformation, but at a slightly different frequency, one
finds
a broad resonance associated with chaotic rays that can classically
diffuse
to regions in phase space where escape is easiest, namely the bottom
of
the plot. In this region, trajectories impinge on the outer boundary
with
large momentum (χ is
the angle of incidence
with respect to the normal).
 When the deformation is changed by a minute amount, the two states
above are coupled
due to their energetic overlap, and the wave function has weight on
the regular
and chaotic regions alike. This is called
dynamical tunneling because it represents a phase space distribution
that
cannot be generated by a classical trajectory.
When the deformation is changed by a minute amount, the two states
above are coupled
due to their energetic overlap, and the wave function has weight on
the regular
and chaotic regions alike. This is called
dynamical tunneling because it represents a phase space distribution
that
cannot be generated by a classical trajectory.