This is the HTML version of a Mathematica 8/9 notebook. You can copy and paste the following into a notebook as literal plain text. For general notes and other related examples, see this page.
The function listGradientFieldPlot takes a scalar potential on a two-dimensional rectangular grid as its first argument, in the form of a list φ. The lengths corresponding to the grid dimensions can be given through the option DataRange → {{xmin, xmax}, {ymin, ymax}}.
The plot contains three elements:
φ, ∇φ,∇φ (they are everywhere perpendicular to the contour lines of the potential).
Because the potential is given as a list, I could calculate the gradient either from an interpolating function or by using discrete first-order derivatives. In fact, the built-in function DerivativeFilter can be used to calculate directional derivatives of arrays, and it uses interpolation. Some interesting uses of this filter are shown in this blog entry.
Unfortunately, interpolation can introduce artifacts. For example, define a rapidly varying function on a grid by
m = Table[(y^2 + (x - 2)^2)^(-1/2), {x, -1.57, 3.43, .1}, {y, -1.57, 1.43, .1}];
and then execute the test cases
Table[Graphics@Raster[Abs@DerivativeFilter[m, {1, 0}, InterpolationOrder -> i]], {i, 3, 9, 2}]
This will reveal an increasing number of undesirable ripples. Moreover, DerivativeFilter doesn't allow the padding option "Extrapolated" which is needed to get reasonable derivatives at the boundary of a region.
Therefore, to do the gradient of an array, I decided to calculate derivatives without interpolation by means of a standard finite-difference scheme. This is done in the variables delX and delY below, using an auxiliary array that has been padded at the borders using extrapolation.
listGradientFieldPlot[grid_?((Length[Dimensions[#]] == 2) &),
opts : OptionsPattern[]] :=
Module[
{
img,
cont,
densityOptions,
contourOptions,
frameOptions,
plotRangeRule,
delX,
delY,
gridSpacing,
gradField,
gradNorm,
field,
fieldL,
rangeCoords,
maxNorm,
paddedGrid = ArrayPad[grid, 1, "Extrapolated"]
},
gridSpacing = (DataRange /. {opts}).{-1, 1};
If[! NumericQ[Norm[gridSpacing]], gridSpacing = {1, 1},
gridSpacing = gridSpacing/Reverse[Dimensions[grid] - 1]];
densityOptions = Join[
FilterRules[{opts},
FilterRules[Options[ListDensityPlot],
Except[{Prolog, Epilog, FrameTicks, PlotLabel, ImagePadding, GridLines, Mesh, AspectRatio, PlotLabel,
PlotRangePadding, Frame, Axes}]]],
{PlotRangePadding -> None, Frame -> None, Axes -> None,
AspectRatio -> Automatic}
];
contourOptions = Join[
FilterRules[{opts},
FilterRules[Options[ListContourPlot],
Except[{Prolog, Epilog, FrameTicks, PlotLabel, Background, ContourShading, Frame,
Axes}]]],
{Frame -> None, Axes -> None, ContourShading -> False}
];
delX = (RotateRight[paddedGrid, {0, 1}] -
RotateLeft[paddedGrid, {0, 1}])[[2 ;; -2, 2 ;; -2]]/
gridSpacing[[1]];
delY = (RotateRight[paddedGrid] - RotateLeft[paddedGrid])[[2 ;; -2,
2 ;; -2]]/gridSpacing[[2]];
gradNorm = Sqrt[delX*delX + delY*delY];
gradField =
MapThread[{#2, #1} &, {Transpose[delY], Transpose[delX]}, 2];
maxNorm = Max[Abs[gradNorm]];
gradField = Chop[gradField/maxNorm];
fieldL =
ListDensityPlot[gradNorm, Evaluate@Apply[Sequence, densityOptions]];
field=First@Cases[{fieldL},Graphics[__],\[Infinity]];
plotRangeRule = FilterRules[Quiet@AbsoluteOptions[field], PlotRange];
rangeCoords = Transpose[PlotRange /. plotRangeRule];
img = Rasterize[field, "Image"];
cont = If[
MemberQ[{0, None}, (Contours /. FilterRules[{opts}, Contours])],
{},
ListContourPlot[grid,
Evaluate@Apply[Sequence, contourOptions]]];
frameOptions = Join[
FilterRules[{opts},
FilterRules[Options[Graphics],
Except[{PlotRangeClipping, PlotRange}]]],
{plotRangeRule, Frame -> True, PlotRangeClipping -> True, PlotLabel -> Row[{"Maximum field =", maxNorm}]}
];
If[Head[fieldL]===Legended,Legended[#,fieldL[[2]]],#]&@
Apply[Show[
Graphics[
{
Inset[
Show[SetAlphaChannel[img,
"ShadingOpacity" /. {opts} /. {"ShadingOpacity" -> 1}],
AspectRatio -> Full], rangeCoords[[1]], {0, 0},
rangeCoords[[2]] - rangeCoords[[1]]]
}],
cont,
ListStreamPlot[gradField,
Evaluate@FilterRules[{opts}, StreamStyle],
Evaluate@FilterRules[{opts}, StreamColorFunction],
Evaluate@FilterRules[{opts}, DataRange],
Evaluate@FilterRules[{opts}, StreamColorFunctionScaling],
Evaluate@FilterRules[{opts}, StreamPoints],
Evaluate@FilterRules[{opts}, StreamScale]],
##
] &, frameOptions]
]
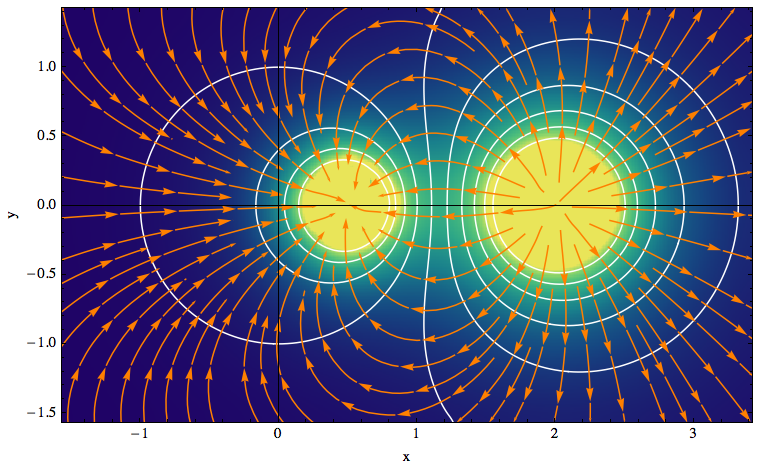
Here is an example of how to use the function. The contour lines of the potential are shown in white, and the streamlines of the gradient field are orange.
grid = Transpose@
Table[(y^2 + (x - 2)^2)^(-1/2) - (y^2 + (x - 1/2)^2)^(-1/2)/
2, {x, -1.57, 3.43, .1}, {y, -1.57, 1.43, .1}];
l1 = listGradientFieldPlot[grid, ColorFunction -> "BlueGreenYellow",
Contours -> 10, ContourStyle -> White, Frame -> True,
FrameLabel -> {"x", "y"}, InterpolationOrder -> 2,
ClippingStyle -> Automatic, Axes -> True, StreamStyle -> Orange,
ImageSize -> 500, DataRange -> {{-1.57, 3.43}, {-1.57, 1.43}}]