About	People	Research	Publications	Software	Data	Blog	Join	Internal
	Why extinction estimates from extant phylogenies are so often zero By Stilianos Louca. May 21, 2021 Background Estimating the rates at which species go extinct is a topic of central importance to the field of paleobiology, evolution and conservation biology. For many taxa, such as bacteria and many soft-bodied eukaryotes, the fossil record is rather sparse, and hence scientists have turned to alternative sources of information for estimating extinction rates. 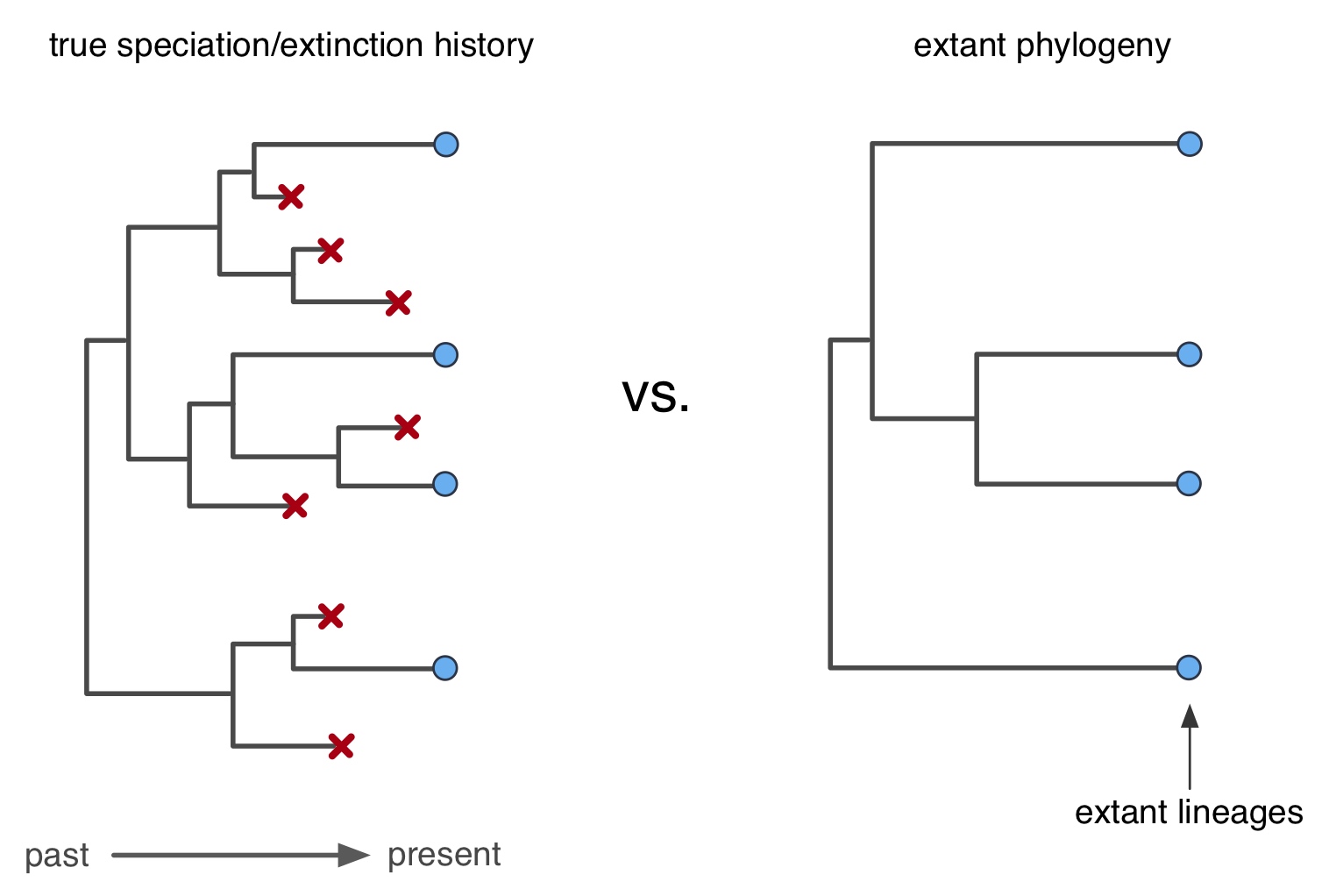A particularly popular approach is to examine the structure of time-calibrated phylogenetic trees encoding the evolutionary relationships between extant species ("extant timetrees"). Most commonly, researchers use extant timetrees to fit so called "birth-death" models using a technique known as "maximum-likelihood". In these models, speciation ("birth") and extinction ("death") events occur stochastically according to some rates (λ and μ, respectively) that may vary over time, and the goal of fitting these models is to reconstruct the historical rates of extinction and speciation. Despite the popularity of such approaches, there has been an ensuing conundrum that has never been satisfactorily resolved: Extinction rates estimated from extant timetrees are suspitiously often zero, contradicting the widespread observation in the fossil record that extinction is widespread and that the vast majority of species ever to have existed on Earth are now extinct. Numerous attempts have been made to explain why extinction rates may be wrongly estimated, all of which essentially invoke some type of model inadequacy argument, i.e. the argument that our current models are insufficient for capturing one or more aspects the true speciation/extinction processes. While model inadequacy is in and of itself probable, it is not clear why one should specifically obtain zero extinction rate estimates so often. In addition, it turns out that even when our models are adequate, i.e. cannot be rejected based on the data at hand, one still frequently obtains erroneous zero extinction estimates. Mathematical breakthroughs bring the answer within reach In a paper recently published in the journal Current Biology, we provide a surprisingly simple and elegant explanation for this mystery. Our explanation is based on mathematical breakthroughs that we had previously published in the journal Nature (2020). Specifically, we had mathematically shown that for any candidate diversification scenario (i.e., with a specific λ and μ, which may vary with time) there exist a myriad of alternative and markedly different diversification scenarios that would generate extant species timetrees with the same probability distribution as the candidate scenario. These "congruent" diversification scenarios are statistically indistinguishable from the candidate scenario, even for infinitely large datasets. In practice, this means that when fitting specific birth-death models to an extant species timetree (for example via maximum likelihood), we can at most recover the congruence class (i.e., the set of all congruent scenarios) of the true diversification history that generated the tree, but not the true diversification history itself. In particular, extinction rates estimated on the sole basis of extant timetrees and in the absence of any additional information are almost always going to be wrong. 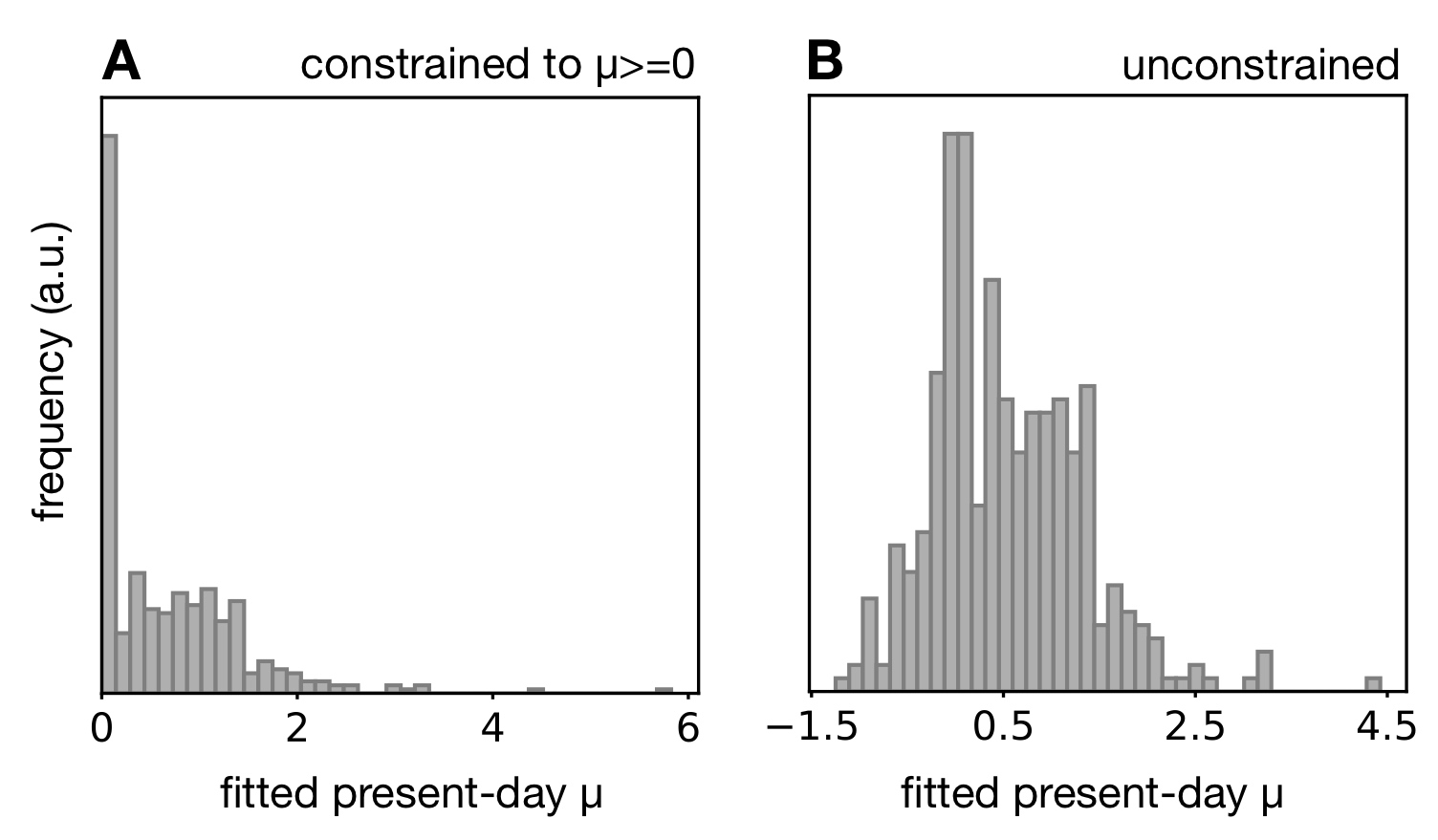Why then are the (erroneous) extinction rates estimated from extant timetrees and reported in the literature so often zero, rather than continuously and randomly distributed positive numbers, in other words, why are published extinction rate estimates "zero-inflated"? 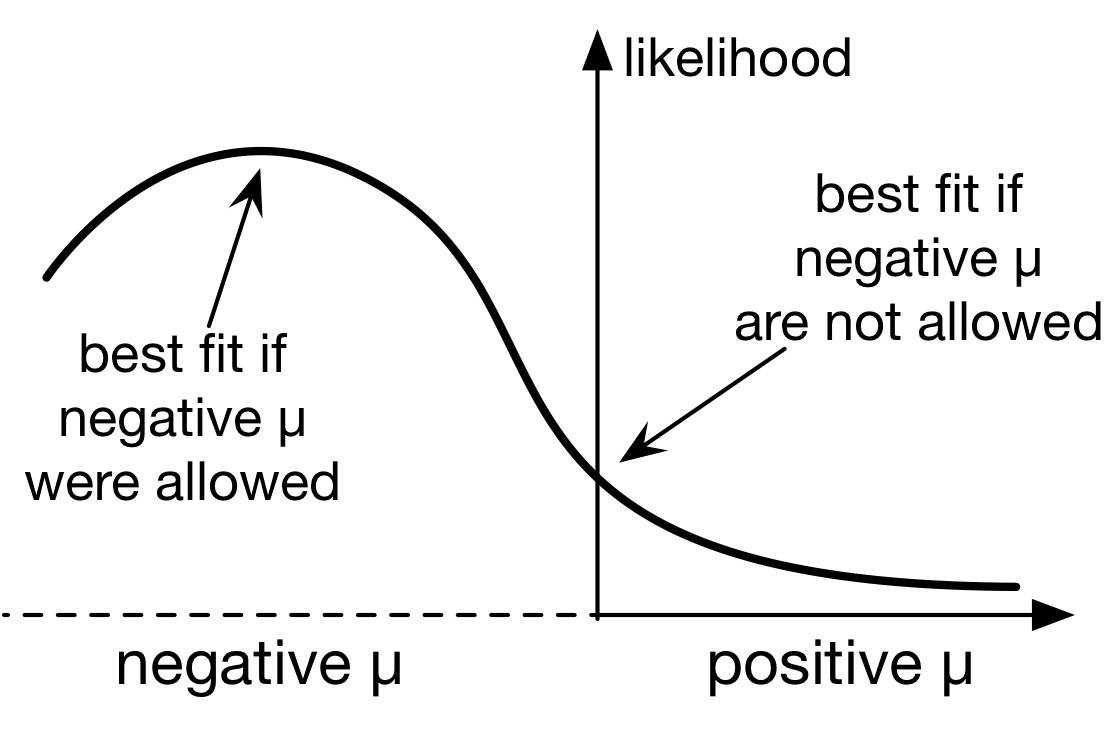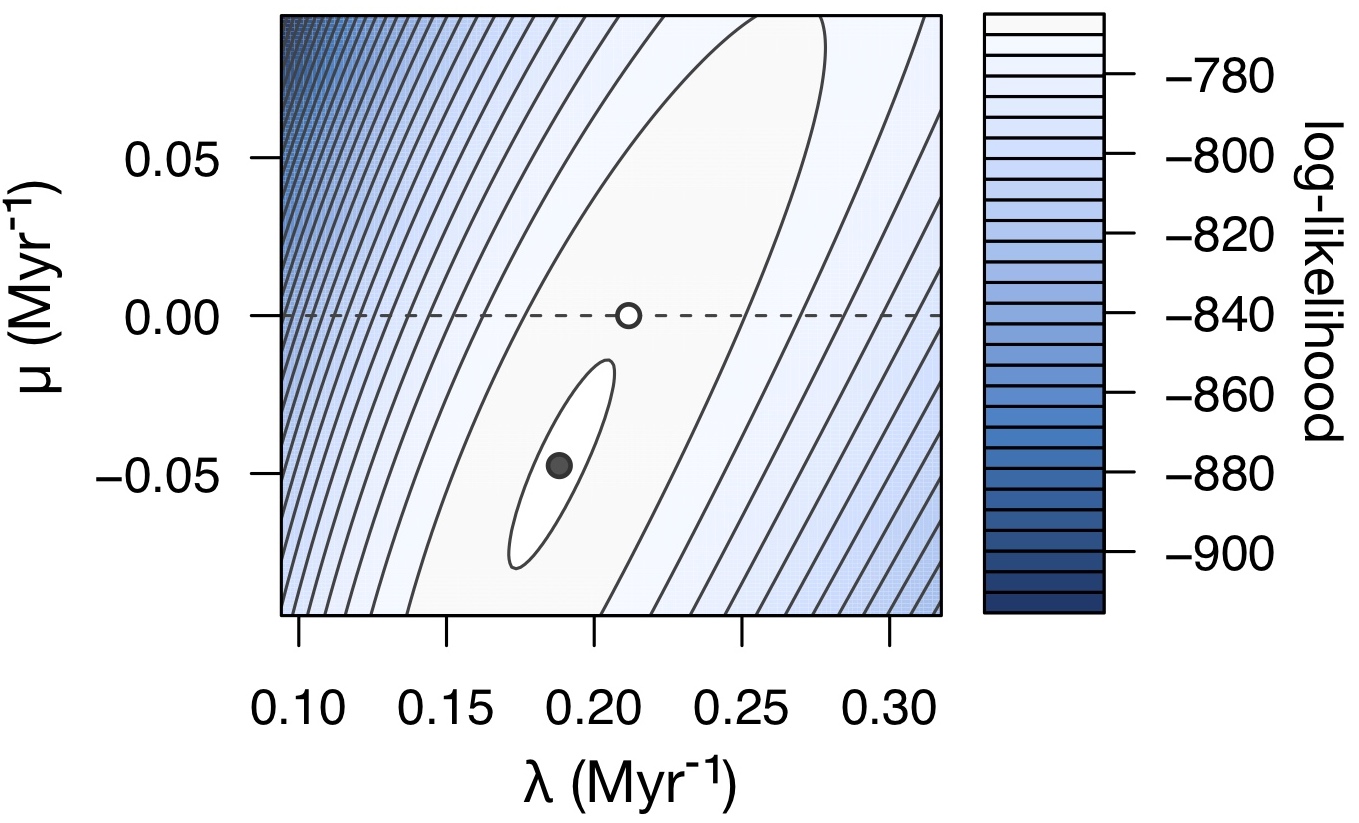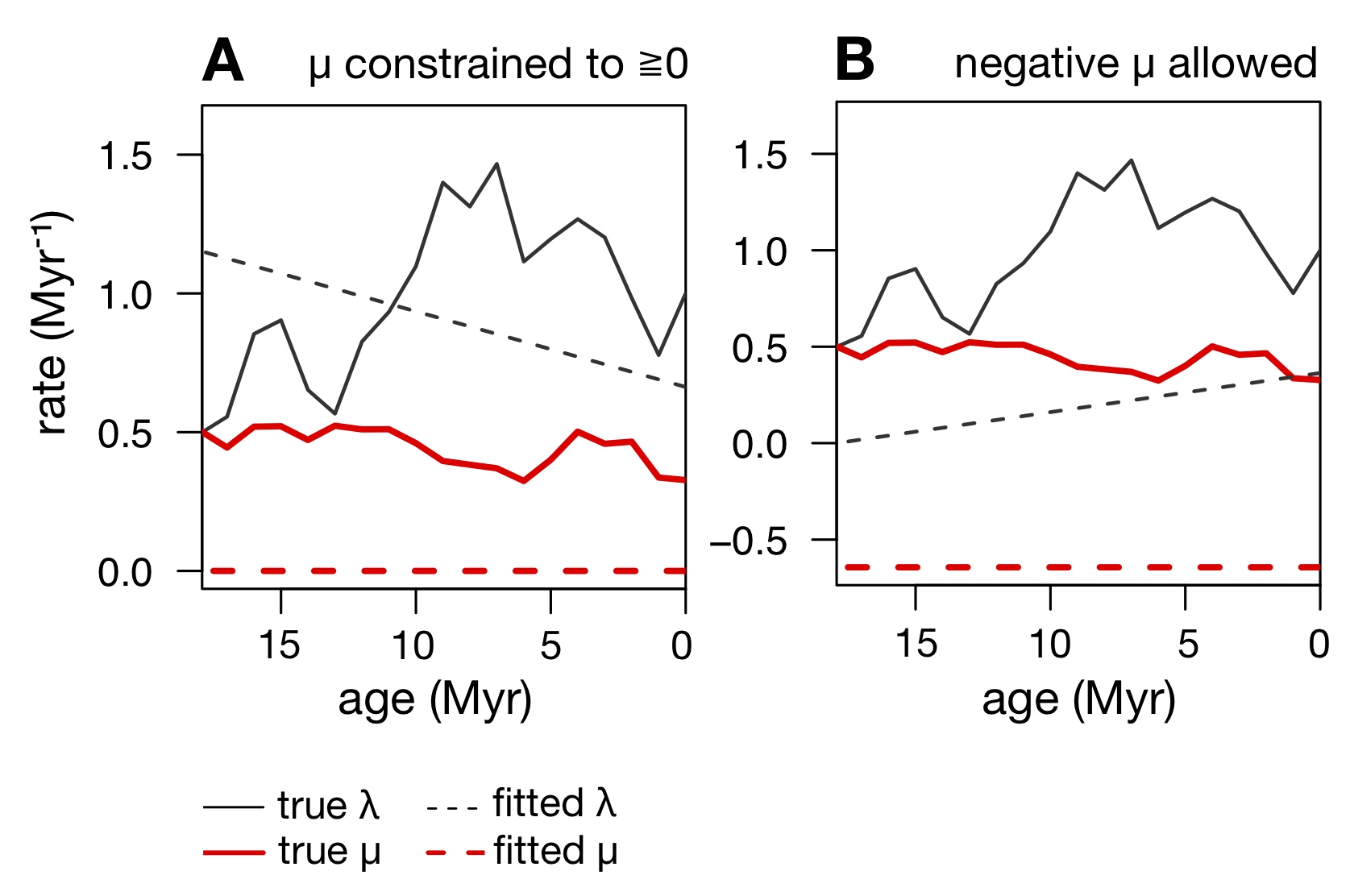It turns out that the answer to this mystery stems from the fact that the likelihood function of a birth-death model (which plays a central role in model fitting) is mathematically well-defined even for extinction rates that are negative (μ<0). If one were to also consider models with negative μ, then the congruence class of the true historical diversification scenario would include many scenarios with partly or fully negative μ. Such scenarios are of course biologically meaningless, but if one were to permit such scenarios, it could often be the case that such a scenario is "closest" to the true congruence class (i.e., has the highest likelihood) among the set of considered scenarios, even compared to those scenarios with positive μ. This is not paradoxical once one recognizes that what one is really estimating is the congruence class of the true diversification history and not the true diversification history itself, and that any scenario with negative μ is congruent to a myriad of scenarios with positive μ. However, imposing the biologically motivated constraint that μ be non-negative, as is typically done, places a boundary in parameter space that one tends to run up against, thus yielding estimates for μ that are zero simply because zero provides the next-best fit compared to a negative μ (illustration on the right). A similar issue also arises when using Bayesian statistics, insted of the maximum-likelihood approach described so far. While the above explanation seems plausible in principle, it was never considered before because the existence and implications of a myriad of congruent birth-death models (including with negative μ) was not known until recently. Confirming the validity of our explanation To confirm the validity of this explanation and its relevance to realistic situations, we considered 6 non-trivial testable predictions that would necessarily apply when fitting birth-death models via maximum-likelihood, and then tested these predictions using numerical simulations as well as empirical phylogenies from 109 eukaryotic taxa. 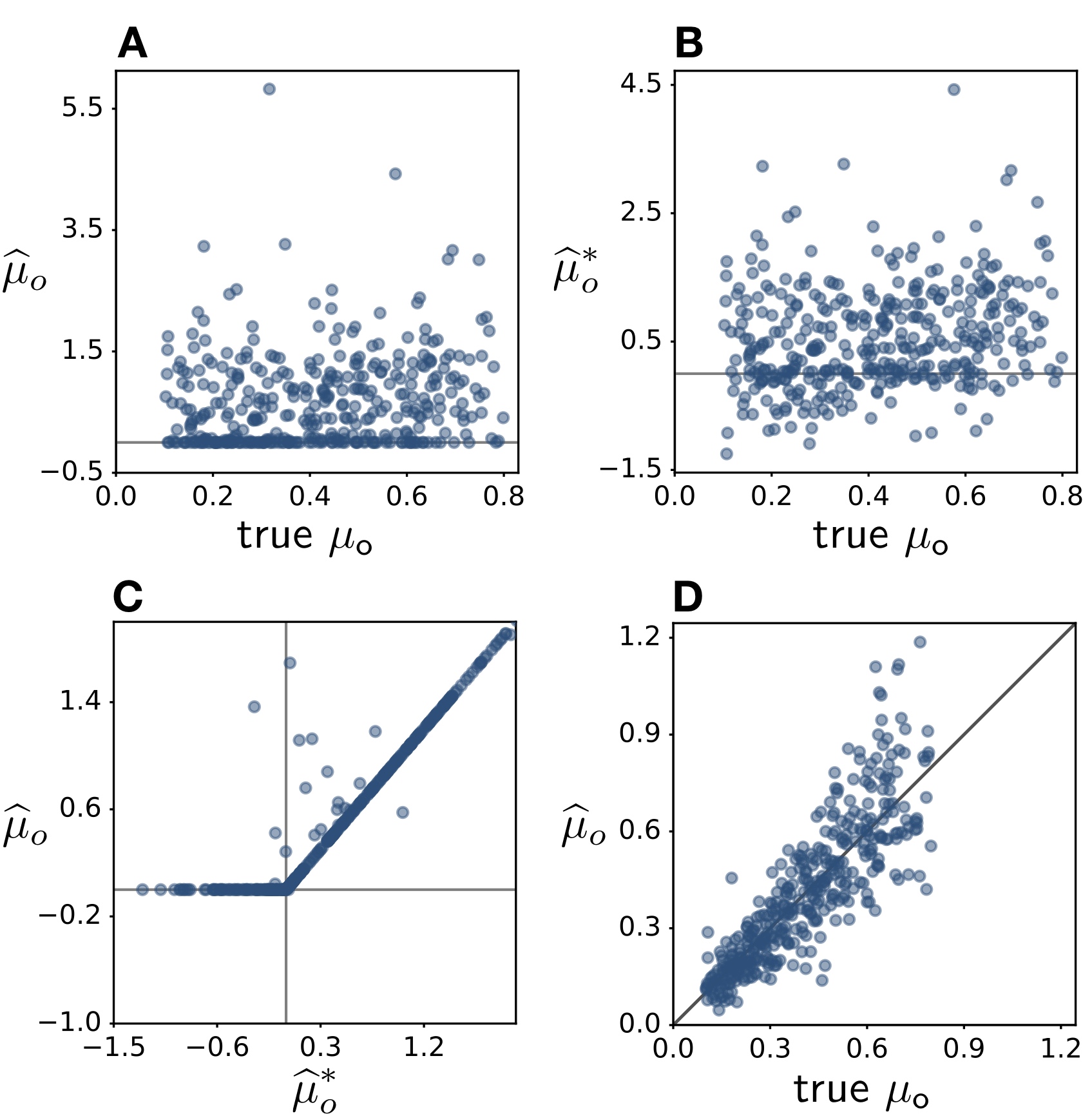For example, we predicted that in almost all cases where μ is erroneously estimated to be zero at one or more time points, one should obtain negative extinction rate estimates if these were allowed. In particular, when allowing negative μ, the distribution of estimated μ should no longer be zero-inflated. Reciprocally, estimating a negative μ (if allowed) should increase the chances of obtaining a zero extinction rate estimate when constrained to non-negative values. Further, fixing the speciation rate λ to its true value during fitting, which "collapses" the congruence class to a single scenario, should yield much more accurate estimates of μ and should eliminate their zero-inflation. As we explain in our Current Biology paper, we fully confirmed these and our other 4 predictions. Implications It is probable that other mechanisms also lead to errors in extinction rate estimates, but these mechanisms don't adequately explain the zero-inflation of extinction rate estimates, and our analysis of empirical trees suggested that model inadequacy was not an important cause of zero-inflated extinction estimates in practice. Regardless of whether our proposed mechanism is the main cause of zero-inflated extinction estimates, it is clear that very erroneous zero-inflated extinction estimates are probable even without detectable model inadequacies and even for large datasets. We thus conclude that most estimates of zero extinction from extant species timetrees seen in the literature are almost certainly wrong. Whether these issues can ever be resolved remains to be seen; it is clear that timetrees of extant species alone are generally insufficient for estimating μ or even testing simple hypotheses about μ such as whether μ was non-zero, without additional constraints. Ultimately this limitation might be resolved with other sources of information, such as population-genetic data, fossils or other biological tracers, and models integrating such information. Full article: Louca, S., Pennell, M.W. (2021). Why extinction estimates from extant phylogenies are so often zero. Current Biology 31:3168-3173 Commentary by Luke Parry: Parry, L. (2021). Evolution: No extinction? No way! Current Biology. 31:PR907-R909. × × × × × × Louca lab. Department of Biology, University of Oregon, Eugene, USA © 2024 Stilianos Louca all rights reserved