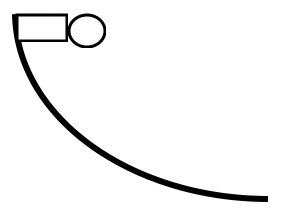
Demonstration 1: A skateboarder is at the top of a curved ramp shown on the right. Assume that friction is so small that it may be neglected. She glides down the ramp to the bottom.

Indicate with a letter from A to F on the diagram on the right the positions where her A. kinetic energy is maximum, B. kinetic energy is minimum, C. potential energy is maximum, D. potential energy is minimum, E. total energy is maximum, F. total energy is minimum.

Only after you have made your predictions, open the Energy Skate Park: Basics simulation: https://phet.colorado.edu/sims/html/energy-skate-park-basics/latest/energy-skate-park-basics_en.html

Select the Friction simulation. Then select the correct ramp, set Friction to None, and select Bar Graph. Drag the skateboarder to the top of the ramp and observe the energy bars as she skates down. (You can repeat the motion by clicking on the skateboarder in the green box at the top.) Indicate your observations on the right in a different color ink.

Compare your observations to your predictions and explain any differences. Is kinetic energy conserved? Is potential energy conserved? Is total energy conserved?

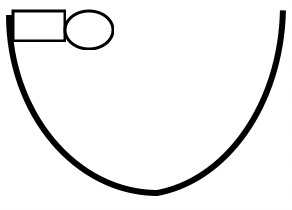
Demonstration 2: The skateboarder now goes on a u-shaped ramp. Again, friction is so small that it may be neglected. She glides down the ramp and then back up the other side.

Indicate with an X on the diagram the maximum height she reaches on the way back up.

Indicate with a letter from A to F on the diagram on the right the positions when her A. kinetic energy is maximum, B. kinetic energy is minimum, C. potential energy is maximum, D. potential energy is minimum, E. total energy is maximum, F. total energy is minimum.

Only after you have made your predictions, use the Energy Skate Park: Basics simulation to make your observations. Select the correct ramp. Be sure that Friction is still set to None. Indicate your observations on the right in a different color ink.

Compare your observations to your predictions and explain any differences. Is kinetic energy conserved? Is potential energy conserved? Is total energy conserved?

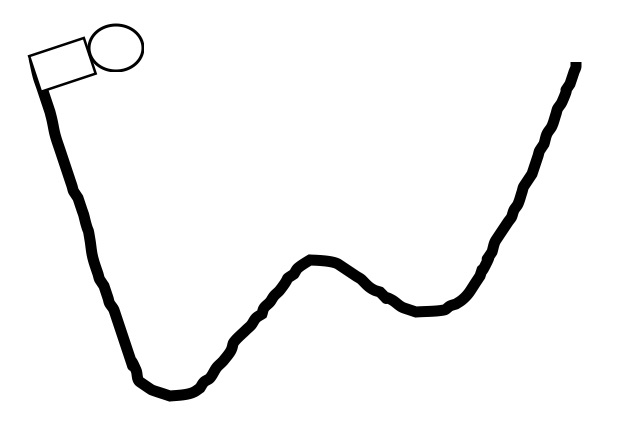
Demonstration 3: The skateboarder now goes on the ramp shown on the right. Again, friction is so small that it may be neglected. She glides down the ramp, up and down the hump and then up the other side.

Indicate with an X on the diagram the maximum height she reaches on the way back up.

Indicate with a Y on the diagram the point where her speed is the fastest.

Indicate with a letter from A to F on the diagram on the right the positions when her A. kinetic energy is maximum, B. kinetic energy is minimum, C. potential energy is maximum, D. potential energy is minimum, E. total energy is maximum, F. total energy is minimum.

Only after you have made your predictions, use the Energy Skate Park: Basics simulation to make your observations. Select the correct ramp. Be sure that Friction is still set to None. Select both Bar Graph and Speed. Indicate your observations on the right in a different color ink.

Compare your observations to your predictions and explain any differences. Is kinetic energy conserved? Is potential energy conserved? Is total energy conserved?

Explain why she is moving fastest at the point you observed.

Demonstration 4: The skateboarder now goes back on the ramp in Demonstration 1 shown again on the right. Something has happened to her wheels, and her skateboard now has significant friction. She glides down the ramp.

As before, indicate with a letter from A to F on the diagram on the right the positions when her A. kinetic energy is maximum, B. kinetic energy is minimum, C. potential energy is maximum, D. potential energy is minimum, E. total energy is maximum, F. total energy is minimum.

How will her speed at the bottom of the ramp compare to her speed in Demonstration 1, without friction?

Only after you have made your predictions, use the Energy Skate Park: Basics simulation to make your observations. Select the correct ramp. First repeat Demonstration 1 (Friction is set to None but with Speed meter also selected. Mark 1 on the speed meter on the right to indicate her speed at the bottom.

Now set Friction to Lots, and repeat, marking the speed at the bottom on the speed meter with a 2.

Also indicate your observations A to F on the ramp on the right in a different color ink.

Compare your observations to your predictions and explain any differences. Is kinetic energy conserved? Is potential energy conserved? Is total energy conserved? What other form of energy must be included in Total Energy now, and how does it affect the kinetic energy of the skateboarder at the bottom?

Demonstration 5: The skateboarder goes back to the u-shaped ramp in Demonstration 2 with her damaged skateboard (significant friction). She glides down the ramp and then back up the other side.

Indicate with an X on the diagram the maximum height she reaches on the way back up.

Describe what will happen if she continues to go up and down, from one side to the other.

Only after you have made your predictions, use the Energy Skate Park: Basics simulation to make your observations. Select the correct ramp. Set Friction to Lots, start her at the top left, and observe what happens. Let the simulation run long enough for her to go up and down a number of times.

Indicate with a different color X the actual height she reaches on the way back up the first time. Did this agree with your prediction? Explain why she reaches this height.

What happens to the skateboarder after a long time? Did this agree with your prediction? Explain. 

Is kinetic energy conserved? Is potential energy conserved? Is total energy conserved? What happens to the potential and kinetic energy of the skateboarder as she glides along the ramp? Why? Where does her energy go?