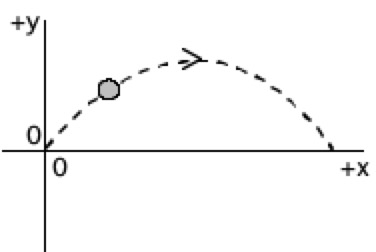
These demonstrations involve a ball thrown in the air with an initial velocity upward and to the right. First observe the motion by clicking BallToss to download and then play the video.

As you see in the video, the trajectory of the ball looks approximately like the sketch to the right.  Note that the origin of the coordinate system has been chosen to be the initial position of the ball.

Demonstration 1: Sketch on the axes on the right your predictions for the x coordinate of the ball as a function of time and the y coordinate of the ball as a function of time.

Only after you have made your predictions, click Position to display a video with the Position-time graphs plotted out as the ball moves.  Compare the actual x and y position graphs to your predictions and explain any differences.

Based on your graph of x vs. t, write a kinematic equation for x as a function of time.

 x = ______________________

Based on your graph for y vs. t, write a kinematic equation for y as a function of time. 

y = _______________

Only after you have made your predictions, click here to see the graphs of x and y vs. time. Compare to your predictions, ands explain any differences. Explain the meaning of each term in the equations.

Question 1: When is the speed of the ball a maximum? A minimum?

Question 2: At the highest point in its motion, is the speed of the ball zero?

Question 3: When is the x-component of the velocity a maximum? A minimum?

Question 4: When is the y-component of the velocity a maximum? A minimum?

Demonstration 2: On the axes to the right, sketch your predictions for the x-component of the velocity as a function of time and the y-component of the velocity as a function of time.

Only after you have made your predictions, click Velocity to display a video with the Velocity-time graphs plotted out as the ball moves.  Compare the actual vx and vy velocity graphs to your predictions and explain any differences.

Based on your graph for vx vs. t, write an equation for vx as a function of time. 

vx = ______________________

Based on your graph for vy vs. t, write an equation for vy as a function of time. 

vy = ______________________

Only after you have made your predictions, click here to see the graphs of vx and vy vs. time. Compare to your predictions, ands explain any differences. Explain the meaning of each term in the equations.

Question 5: In the space below, draw an arrow that represents the direction of the acceleration of the ball (a) just after it is released, (b) when it reaches the highest point in its trajectory, (c) while it is on its way down.  If the acceleration is zero, write ZERO above the ball.

Only after you drawn your arrows, click here to see the correct answers

Question 6: In the space below, draw the free-body (force) diagram for the ball (a) just after it is released, (b) when it reaches the highest point in its trajectory, (c) while it is on its way down. If there are no forces acting on the ball, write NONE above the ball.  If the net force on the ball is zero, write ZERO above the ball

Only after you drawn your arrows, click here to see the correct answers