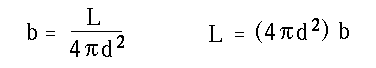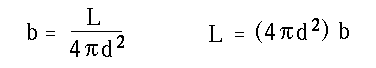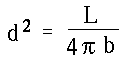Luminosity and how far away things are

The luminosity is how much energy is coming from the per second. The units are watts (W).

Astronomers often use another measure, absolute magnitude. Absolute magnitude is based on a ratio scale, like apparent magnitued. I think it is confusing.

The luminosity of the Sun is

Apparent brightness

The apparent brightness is how much energy is coming from the star per square meter per second, as measured on Earth. The units are watts per square meter (W/m²).

Astronomers usually use another measure, magnitude. (Our book calls it apparent magnitude.) Since magnitude is so commonly used, we need to understand a little about it too. The magnitude system stems from ancient Greece. A very bright star was called ``first magnitude,'' a pretty bright star is ``second magnitude,''... a barely visible star is ``sixth magnitude.''

Measuring luminosity

• the distance d to the star,
• the apparent brightness b of the star, and
• the luminosity L of the star.

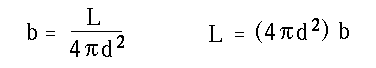
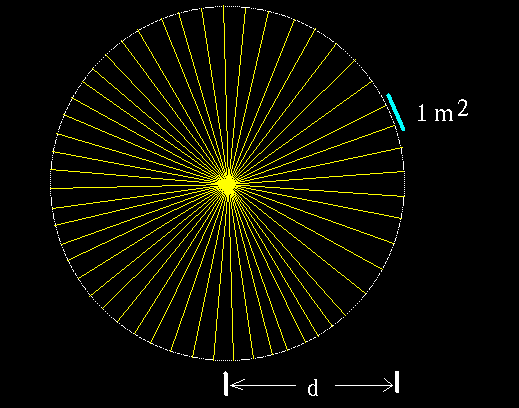
This relation is based on conservation of energy. Consider an observer a distance d from the star. How much energy crosses a square meter detector that this observer has?

• All of the energy produced by the star per second must cross a sphere of radius d.
• The study of geometry tells us that area of this sphere is 4 Pi d².
• a 1 m² detector gets a fraction
  (1 m²)/(total area)
  of this.

Note that the brightness decreases proportionally to the square of the distance as one moves away from the star. This can be demonstrated experimentally in the laboratory.

We can write the relation so that it gives L in terms of b and d.

• It is easy to measure the apparent brightness b (e.g. with a telescope and a CCD).
• It is not so easy to measure the distance, but we have already seen something about how that can be done.
• Putting these toghther, we get L.

Luminosities of stars

• There are a few stars that are more luminous than the Sun.
  • For instance, Betelgeuse has L ~ 14000 x L_sun.
• Most stars are less luminous than the Sun.
  • For instance, L_star ~ 0.001 x L_sun is not unusual.
• There are lots more low luminosity stars than high luminosity stars.

Using brightness and luminosity to get distance

• It is easy to measure the apparent brightness of a star, a galaxy, a supernova, ...
• If somehow we know the luminosity of such an object, then we can compute its distance from us.
  
  
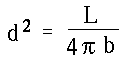
• This is the essence of how we learn the distances to things.
• Example: You have a 100 W lightbulb in your laboratory. Standing a distance d from the lightbulb, you measure apparent brightness of the lightbulb to be 0.1 W/m². How can you use this information to determine the distance from you to the lightbulb? (An approximate answer is OK. In particular, you can approximate 4 Pi = 12.566 by 10.)
  
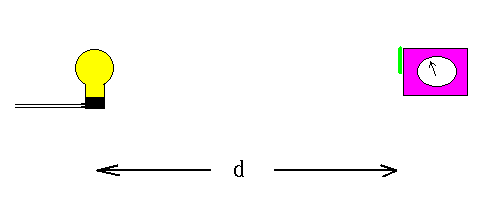
  1. The luminosity of the lightbulb is L = 100 W.
  2. The brightness is b = 0.1 W/m².
  3. So the distance is given by d² = (100 W)/(4 Pi x 0.1 W/m²).
  4. Since 4 Pi is approximately 10, this is d² = (100 / 1) m².
  5. Thus d² = 100 m².
  6. We now know what d² is. We want to know what d is. So we take the square root.
  7. So d = 10 m.
• Example: You see a 1000 W streetlamp on a distant hill. You measure the apparent brightness of the streetlamp to be 0.000001 W/m². How can you use this information to determine the distance to the hill? (An approximate answer is OK. In particular, you can approximate 4 Pi = 12.566 by 10.))
  
  1. The luminosity of the streetlamp is L = 1000 W = 10³ W.
  2. The brightness is b = 0.000001 W/m² = 10^-6 = W/m².
  3. So the distance is given by d² = (10³ W)/(4 Pi x 10^-6 W/m²).
  4. Since 4 Pi is approximately 10, this is d² = (10³ /(10 x 10^-6)) m².
  5. Thus d² = (10³ / 10^-5) m².
  6. So d² = 10⁸ m²
  7. We now know what d² is. We want to know what d is. So we take the square root.
  8. So d = 10⁴ m = 10 km.