Mass Measurement

How to measure mass.

Suppose that an object, say a star, is in a circular orbit about a small object with a much bigger mass (say a big star).

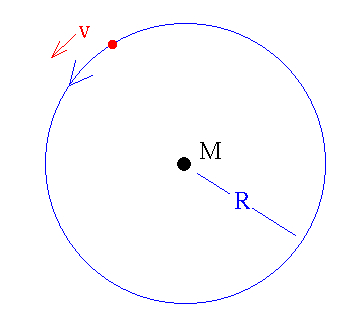
Let M be the mass of the big star in the center.
Let R be the radius of the small star's orbit.
Let v be the velocity of the small star in it's orbit.

If we measure R and v, then we can determine M from

Example

Radius of Earth's orbit = 1.5 x 10¹¹ m.
Speed of Earth in its orbit = 3.0 x 10⁴ m/s.
G = 6.67 x 10^-11 m³ kg^-1 s^-2.
So the mass of the Sun is
M_sun = (1.5 x 10¹¹ m) x (3.0 x 10⁴ m/s)² /(6.67 x 10^-11 m³ kg^-1 s^-2)
= (1.5 x 10¹¹ x 9.0 x 10⁸/(6.67 x 10^-11 ) kg
= 2.0 x 10³⁰ kg
This is how we know the mass of the Sun.

There is more general formula that covers the case that the mass of the central star is not much bigger than that of the orbiting star and to cover the case of eliptical orbits. However, we will stick to a light object orbiting a heavy object in a circular orbit.

What if the heavy object isn't small?

Suppose that our light star is orbiting a mass distribution that is spread out over a vast region of space instead of being concentrated at a point in the middle.

All of this mass pulls on our star.

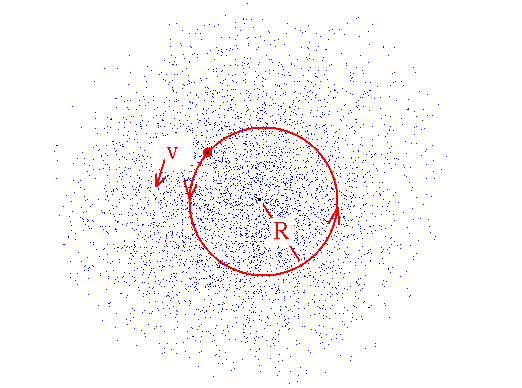
In general, this is complicated. But it is simple if the mass distribution is spherically symmetric.

Then the same formula holds,

with

M = mass inside radius R.
If the mass distribution is not spherically symmetric, then we have to correct to account for its non-spherical shape.

Davison E. Soper, Institute of Theoretical Science, University of Oregon, Eugene OR 97403 USA soper@bovine.uoregon.edu