What is the final end stage of the core of a star?

During star life, something is always happening that can't go on forever. For instance, the star may be burning a nuclear fuel.

What can be the final stable state of a star core? This is a question for theoretical analysis. Once we figure out where a star can get to, we can investigate how it can get there. Then we can look for the observational evidence.

M < 1.4 Msun

Normally, matter doesn't have to be hot to hold itself up against gravity. It just has to be dense enough. The amount of mass in the star core determines the needed central pressure. The needed pressure determines the needed density.

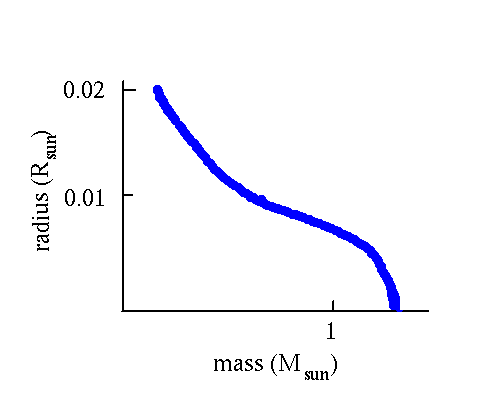
For masses on the order of a solar mass, the pressure is provided by the electrons, which don't like to be squeezed to tightly together. The theory is rather simple. Here is a graph of the result:

The density in the center of the dead star is very high, on the order of 109 kg/m3. The temperature will typically be high too, until the star (very gradually) cools off. But the temperature doesn't matter for this graph.

Are there real objects like this?

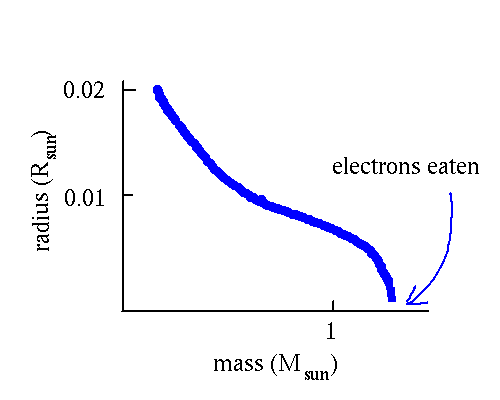
Note that the radius of the star gets smaller as more mass is added. For a mass greater than 1.4 Msun there is no size at which the stellar core is stable. Thus there is a limit to the mass that a white dwarf can have. The limit is called the Chandrasekar limit.

[Subrahmanyan Chandrasekhar won the 1983 Nobel prize for his studies of white dwarf stars. He was born in India and worked at the University of Chicago.]

1.4 Msun< M < 3 Msun

The graph above for the size of a white dwarf as a function of its mass leaves out an important process. The graph assumes that the electrons that provide the pressure do not have any interactions.

The enormous pressure of the electrons can be thought of as being due to the star trying to put too many particles in too small a space. Solution: get rid of particles.

proton + electron --> neutron + neutrino

The neutrino escapes, leaving just a neutron. The electron is gone.

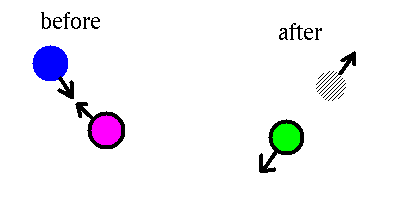
Thus we revise our picture:

For masses above the Chandrasekar limit, we should work out what the radius versus mass would be for a cold ball of neutrons. Here is the result:

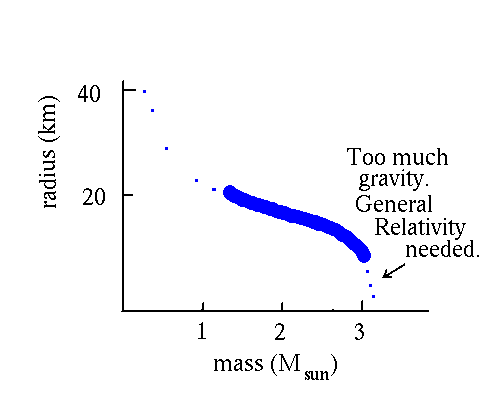
The prediction is that there should exist neutron stars with masses in the range 1 to 3 Msun and sizes about 10 km.

Are there real objects like this?

M > 3 Msun

The graph above for the size of a neutron star as a function of its mass is based on Newton's theory of gravity. It seems to have a limiting mass of about 3 Msun, similar to the Chandrasekar limit.

But to get it right, a better theory of gravity is needed. The better theory is thought to be the General Theory of Relativity (A. Einstein, ca 1918).

One feature is that gravity bends light. The more mass there is inside a small sphere, the more light is bent.

There is a limit.

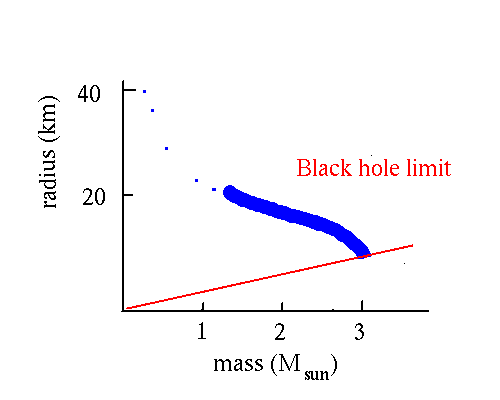
What general relativity says is that if the radius of the star gets smaller than the limit (known as the Schwarzschild radius), then

What happens to the star?

In a sense, it doesn't matter, since no evidence about what happens can ever get out.

What happens in theory is that the matter in the star is crushed until it is so dense that ...

...so dense that we don't know what happens.

Are there real objects like this?

Davison E. Soper, Institute of Theoretical Science, University of Oregon, Eugene OR 97403 USA soper@bovine.uoregon.edu