Determining distances through parallax

The apparent position of nearby stars against the background of far-away stars changes as the Earth goes in its orbit around the Sun:

Here is what we see:

We can measure the angle, called the parallax, p of the star:

In this picture we measure the parallax p, we know the size of 1 AU, so we can compute the distance d to the star.

If the distance were twice as far, the parallax would be twice as small:

Thus the relation is

The constant depends on the units used for the parallax angle and for distances (meters, AU, ...).

Astronomers like to measure angles in seconds of arc. (There are 360 degrees in a circle, 60 arc minutes in a degree, 60 arc seconds in an arc minute, see units page .) Then a convenient unit of distance is the unit that makes the constant in this equation equal to 1. This unit is called the parsec. With this unit of angle and distance, the distance fomula is:

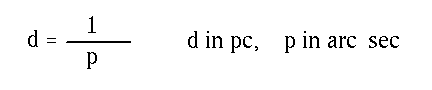
Here, in a picture, is the definition of a parsec:

Since we know how many arc seconds there are in a complete circle, we can work out how many AU there are in a parsec. The result is

1 pc = [(360 x 60 x 60) / (2 Pi) ] x 1 AU = 2.06 x 10⁵AU.

(You need to see that this is simple, but you don't need to be able to derive it.)

Since we know that 1 AU = 150 x 10⁶ km, we find

1 pc = (2.06 x 10⁵) x (150 x 10⁶) km.

This is

1 pc = 3.09 x 10¹³ km.

One also hears astronomical distances expressed in light-years. A light year is how far light goes in one year. It is

1 ly = 0.3 pc.

With space based observations, the parallax method of determining distances works out to about 200 pc. (From a satellite, we don't have to contend with smearing of stellar images by turbulence in the atmosphere.) There are nearly a million stars within 200 pc of us.

ASTR 122 course home page

Updated 22 Octobber 2007