14. 方波和矩形波
电子音乐互动教材中介绍的最后两种常见复杂波形是 方波 和 锯齿波。从它们的名字中你可能就能看出,这两种波形是相关联的,但是方波和矩形波也是两种不同的波形。方波具有以下的特点:
| 频率分量 | 奇数谐波分量 |
| 相应谐波振幅 | 1/谐波级数 |
| 相位 | 所有谐波同相 |
方波的频谱由于 占空比 的缘故只包括谐波序列中奇数序列或者偶数序列。占空比是在时间轴上方的波形占一个周期波形的百分比。方波的占空比是50%,或者说1/2。正因为占空比是1/2,所以每隔一个谐波分量会缺失。
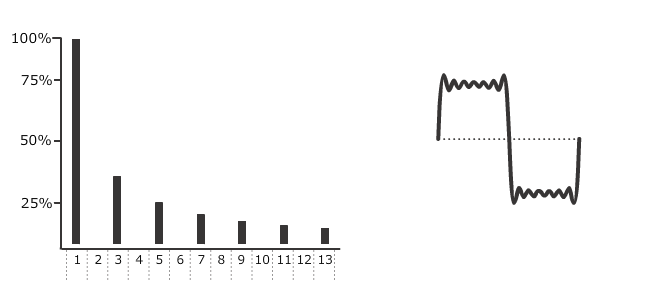
范例 14-1: 常见复杂波形方波的构建。
如果占空比不是50%,那么结果就是一个矩形波。矩形波也叫 脉冲波,占空比可以是除了50%以外的任何数字,但是正如方波,他的谐波谱决定了占空比。比如,矩形波的占空比是25%,1/4,相应的波谱中缺少4的倍数的谐波分量。如果占空比是20%,1/5,相应的波谱中缺少5的倍数的谐波分量。如果占空比是12.5%,1/8,相应的波谱中缺少8的倍数的谐波分量。
谐波波谱
波形�
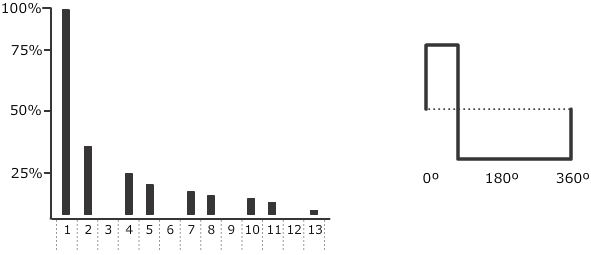

图表 14-2: 矩形波。
方波和矩形波相应的振幅与锯齿波的相同。也就是说一次谐波的相应振幅是1/1,也就是1,第二个频率分量的振幅强度也对应于相应的谐波级数。
将不同频率,振幅和相位的正弦曲线相加,音乐家几乎可以制作出任意多的波形。然而运用这种方法制作声音面临一个实际问题,需要用很多的时间列举出所有的频率分量。
然而合成复杂波形是有捷径的。电子音乐家可以由已保存的复杂波形开始创作从而省略费时间的复杂波形构建过程。