14. 方波和矩形波
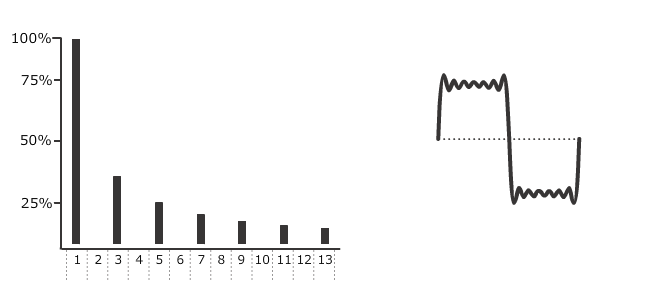
電子音樂互動教材中介绍的最後兩種常見複雜波形是方波和鋸齒波。從它們的名字中可能看出這兩種波形是相關聯的,但方波和矩形波也是兩種不同的波形。方波具有以下的特點:
| 頻率分量 | 奇數諧波分量 |
| 相應諧波振幅 | 1/諧波級數 |
| 相位 | 所有諧波同相 |
方波的諧譜由於佔空比的緣故只包括諧波序列中奇數序列或者偶數序列。佔空比是在時間軸上方的波形佔一個週期波形的百分比。方波的佔空比是50%,或者說1/2。正因為佔空比是1/2,所以每隔一個諧波分量會缺失。
範例14-1:常見複雜波形方波的建構。
如果佔空比不是50%,那麼結果就是一個矩形波。矩形波也叫脈衝波,佔空比可以是除了50%以外的任何數字,但是正如方波,它的諧波譜决定了佔空比。比如,矩形波的佔空比是25%,1/4,相應的波譜中缺少4的倍數的諧波分量。如果佔空比是20%,1/5,相應的波譜中缺少5的倍數的諧波分量。如果佔空比是12.5%,1/8,相應的波譜中缺少8的倍數的諧波分量。
諧波譜
波形
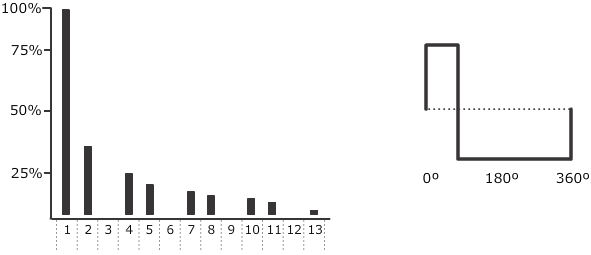

圖表14-2:矩形波。
方波和矩形波相應的振幅與鋸齒波相同。也就是說一次諧波的相應振幅是1/1,也就是1,第二個頻率分量的振幅强度也對應在相應的諧波級數。
將不同頻率,振幅和相位的正弦曲線相加,音樂家幾乎可以制作出多變無限數量的波形。然而運用這種方法制作聲音,面臨一個需用很多时間列舉出所有頻率分量的實際問題。
然而此處有捷徑,電子音樂家可以由已保存的複雜波形開始創作從而省略費時間的複雜波形建構過程。