Ring resonators

Reference for this work

J. U. Nöckel, Zylindrische Dielektrika mit einer nichtkonzentrischen Inklusion: ein Modellsystem für Quantenchaos mit Anwendungen in der Mikrophotonik, talk presented at the Sixth Mie Seminar "Theory of Lightscattering and its Application". Ring resonators, especially in deep-etched Indium Phosphide, were one of the main topics of my work at Nanovation Technologies, 2000-2001.

Rings as annular billiards

Ring resonators have found widespread use in nanophotonics because their operating principle is extremely easy to understand, and many of their properties can be described with the same concepts that apply to one-dimensional optical waveguides, where light is allowed to propagate freely in one direction and confined in the other (transverse) directions. The ring is a waveguide bent back on itself to form a loop. One then can characterize the propagation loss, bend loss and coupling to adjacent waveguides. In a perfectly circular ring, the curvature introduces a centrifugal potential that can effectively be modelled as a slanted index-of-refraction profile in the waveguide cross section.

An alternative but equivalent view is to describe a circular ring as a layered dielectric with rotational symmetry, and apply generalizations of Mie theory to it. See also the hitchhiker's guide to dielectric cavities. The idea is simply that a ring is nothing but a disk with a hole, and exact solutions can be written down both for disks and holes.

The solutions for circularly symmetric cavities are discussed on the following pages:

But what about non-ideal, deformed rings?

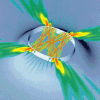
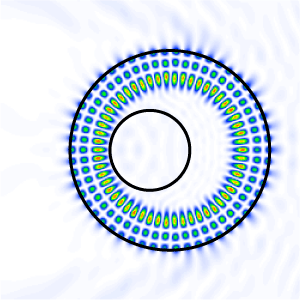
In a wide enough ring waveguide, the inner hole doesn't really have any effect when the circulating modes are pushed to the outer edge by the centrifugal potential. Then, even a non-concentric hole shouldn't worry us at all. This is shown here for a whispering-gallery mode that is just far enough removed from the inner edge to remain essentially undisturbed by the off-center hole.

Ray pictue

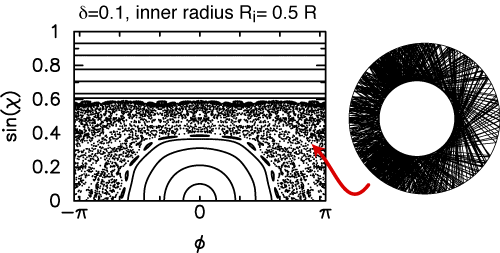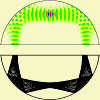
The ray pattern shown here for a non-concentric, closed cavity is chaotic. This can be seen clearly in a Poincaré surface of section, where a two-dimensional cloud of points is generated by a single trajectory.

The solid lines near the top of this surface of section are whispering-gallery trajectories which never feel the inner boundary, and thus behave as if the hole were not there.

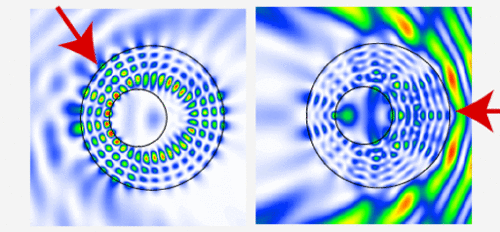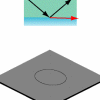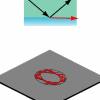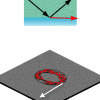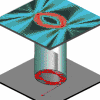
The off-center geometry has preferred coupling directions. This is one of the main reasons why one should be interested in non-circularly symmetric resonator designs. The red arrow indicates the direction of an incoming wave, and the two plots differ only in this choice of direction.

Although the excitation beam is tuned to the frequency of a cavity resonance, there is no coupling into that resonance in the righthand picture. This is because the input beam and cavity mode have opposite parity with respect to the horizontal axis. To learn more about the treatment of discrete symmetries in waveguide and resonator structures, you may want to look at my work on Fano resonances and scattering theory in low-dimensional structures.

Relation to quantum chaos

Rings are not just of great applied interest, but also useful as a model system in quantum chaos. The first paper exploring this connection is discussed here:

Dynamical tunneling in an optical ring resonator

Last modified: Mon Oct 1 14:11:30 PDT 2012