The Drake Equation, Fermi Paradox, and SETI

Chapter 19

Drake Equation

N = R x fs x ne x fl x fi x fc x L

R: average rate of star formation
fs: fraction of stars with planetary systems
ne: numbers of planets in "habitable" zones
 fl: fraction of planets where life develops
 fi: fraction of planets where intelligent life ensues
fc: fraction of intelligent civilizations which want to communicate
L: lifetime of "communicative life"

People have long wondered whether we are unique or not. Frank Drake of Cornell University formulated what is now known as the Drake Equation in 1960 as a way to open the discussion on the possibility of intelligent life in the galaxy. At left is the Drake Equation and the meaning of the terms in the Drake Equation. We consider each term in the Drake Equation and come up with an answer as to the number of intelligent civilizations likely to exist in the Milky Way galaxy. The terms in blue are probabilites and facts which can be deduced from astrophysics. These terms can, in principle, be determined quantitatively. The sections in green are probabilities and numbers which come from biology, psychology, and sociology. These are much more difficult to estimate.

Rate of star formation x Lifetime = # of Stars in the Galaxy:

The number of stars in the Galaxy is determined by the rate at which stars are formed and their lifetimes. We argue why this is so below but first, we give the stellar birthrate for our Galaxy.

As an initial guess, the Milky Way galaxy contains 200 billion stars. If the Milky Way galaxy is ten billion years old, then the average rate of star formation has been

R = 20 stars per year

over the lifetime of the Galaxy. This is roughly correct as most measures for other galaxies suggest that around 10 Solar masses of material goes into star formation per year in typical galaxies. Estimates for our galaxy run from several stars per year to tens of stars. Although, in principle, the star formation rate is potentially the most reliable of the terms in the Drake Equation, it is currently uncertain.

Number of Stars = Rate of Star Formation x Lifetime?

At birth, the galaxy contains no stars. If the rate of star formation is 1 per year and the lifetime of a star is 10 years, let's consider how the stellar population evolves with time.

  • After 1 year, there will be 1 star in the galaxy.
  • After 2 years, a second star will be born and there will be 2 stars in the galaxy.
  • After 3 years, a third star will be born and there will be 3 stars in the galaxy.
  • This continues for 10 years, after which there will be 10 stars in the galaxy.
  • What Happens after the Eleventh Year? Well, an eleventh star was born, but because the lifetime of a star is 10 years, the first star born dies; there remains 10 stars in the galaxy.
  • From hereon, every time a star is born, one dies and the number of stars remains fixed at 10, which we note is

    Number of stars = Rate of Star Formation x Lifetime
The appropriate value for the Lifetime will be discussed later.

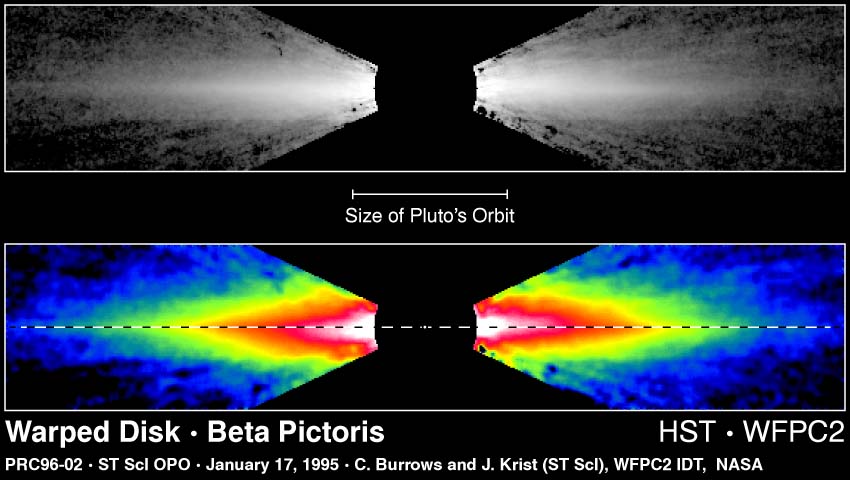
Fraction of stars with planetary systems:

Beta Pictoris is 62.9 light years from the Sun and harbors an A5 V star surrounded a dusty disk which contains the so-called planet b, a Jupiter-sized planet, mass ~ 8 times that of Jupiter, whose orbit is like that of Saturn, 7.6-8.7 Astronomical Units. The bottom images show Planet b as it moved from one side of the disk to the other.

We know that approximately 60 % of all stars are in multiple star systems. Out of double star systems a handful are known to contain planets. Consequently, we suggest that the fraction of stars with planetary systems may be as large as 40-50 %. This, however, assumes that all places where planets can form that they actually do form. Support for the idea that planetary formation is natural and common has gotten stronger over the last 20 years. For a discussion of the techniques used to discover planets go to the NASA Planet Quest link above or here. Around 5,000 extra-solar planets have been discovered in more than 3,500 distinct planetary systems. This suggests that when planetary systems can form, they do form and we estimate that the fraction of stars that have planetary systems is (optimistically)

fp = 0.5

Number of habitable (Terrestrial) planets per planetary system:

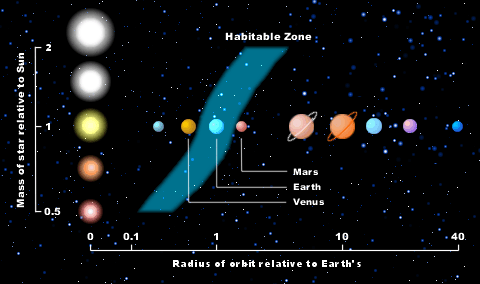The number of detected Terrestrial planets currently numbers in the hundreds. The size of the classical habitable zone is a function of the central star. The classical habitable zones of low mass stars fall near the star. Today, our view of the habitable zone has been extended.

In our Solar System, for Life As We Know It (LAWKI) to form requires a planet with conditions such that liquid water (oceans) may form on or in the planet. The existence of liquid oceans is key to the development of life in most scenarios.
  • For our Solar System, if the energy needed to maintain liquid oceans comes the light received from the Sun, we define the Classical Habitable Zone as the region which strectches from around 0.85 Astronomical Units to (optimistically) 2 Astronomical Units.

  • If we note that other sources of energy are capable of producing liquid oceans, such as tidal heating, a less well-defined Extended Habitable Zone may be defined, one that includes some of the major moons of Jupiter and Saturn.

Artist's rendition of the two Saturn-sized planets in orbit about their star, named Kepler-9. The planets were named Kepler-b and Kepler-9c.

Implicit in the above discussion is that Earth-like planets (necessary for LAWKI) exist in the habitable zones of extra-Solar planetary systems, systems. Important work for discovering Earth-like planets is being performed by the NASA satellite TESS (and was performed by past satellite Kepler). For example, Kepler discovered two transiting planets in one planetary system. The planets are about the mass of Saturn (~1/3 that of Jupiter) with tight orbits, periods 19 days and 38 days. The orbit of Saturn is ~9.6 Astronomical Units and Saturn's orbital period is around 29.5 years. Interestingly, there is evidence for a third planet with Earth-like properties, 1.5 times the mass of the Earth but in an orbit which is only 1.6 days long. The planet is not in the Classical Habitable Zone, however, it orbits way too close to its parent star.

In our Solar System, we have 1-2 planets in our Classical Habitable Zone and Kepler and TESS have discovered roughly a dozen Earth-like planets in the Classical Habitable Zones of their systems. The overall situation is not clear because there are also many Jupiter-like planets known, however the majority of which are hot Jupiters. Let's set (based on our Solar System)

ne = 5

Fraction of Planets on Which Life Develops:

This is hard. If given the opportunity, is the probability that life develops high (is life self-organizing?) or is it low (or is it a more probabilistic process)? As an astronomer, we can test this problem empirically through studies of planets. We don't need to know how the process of how life development works, rather we can simply test to see if when given the possibility for life to know, does it form. In our Solar System, we know places where LAWKI could develop but we don't know if LAWKI has indeed developed. We test this idea. There have been a few searches attempted and further searches planned.

We can also test the idea in extra-Solar planetary systems. For example, for LAWKI, we can pinpoint signatures of life. One of those discussed earlier is the existence of large amounts of free oxygen molecules; our atmosphere is 79 % N2 and 21 % O2. Studies of the atmospheres of extra-Solar planetary atmospheres could strongly imply the existence of life if such signatures are detected.

This is a hard one. Either it is 1 (if life arises from a self-organizing process) or nearly 0 (if life arises randomly), the astronomical picture is not yet clear,

fl = 1 to ~0

Plagiomnium

Fraction of Living Species that Develop Intelligence:

I believe this is 1. If life starts, it will develop intelligence eventually

fi = 1

Fraction of Intelligent Species which Develops Technology and Wants to Communicate:

Again the likely answer is 1 (or could be 0, hard to judge motivation)
fc = 1 - 0

Lifetime of a Technological Civilization:

We first note that the Sun will live for over 10 billion years. The amount of time a star spends in its longest lived phase of nuclear evolution, its Main Sequence phase, is roughly

Lifetime = 10 billion years x Ms-3

where Ms, the star's mass is measured in multiple of the mass of the Sun.

This, however, is not the appropriate lifetime to consider. We must consider the more uncertain lifetime of the length of time an intelligent lifeform has the technological ability and desire to communicate. Using us, humanity as an example, we have had good enough technology (radio) to communicate for 100 years or so. if we use this as a lower limit, then

L = 100 years

The lifetime is hard to estimate, but strongly affects the number of possible intelligent civilizations who wish to communicate with us. If the length of the communication lifetime of a life form is the same as its Main Sequence lifetime then we would expect there to be billions of intelligent civilizations in the Milky Way.

Number of Civilizations that Wish to Communicate:

Plugging everyting into the Drake Equation, we find for the pessimistic guess, N = 0, we are alone, and for the optimistic guess

N = 20 stars per year x 0.5 x 5 x 1 x 1 x 1 x 100 years = 5,000 civilizations

The Drake Equation serves to show that it is not implausible to suggest that there are many other intelligent civilizations who wish to communicate with us in the Milky Way, however, it is also conceivable that we are the only intelligent civilization with such desires.

Marvin

Fermi Paradox

"The apparent size and age of the Universe suggest that many technologically advanced extraterrestrial civilizations ought to exist (see Drake Equation). However, this hypothesis seems inconsistent with the lack of observational evidence to support it."

The Fermi Paradox takes the tact that we wish to argue by contradiction. It is first argued that, although interstellar travel is slow, it is still possible to explore the Milky Way galaxy in several hundred million years, even given our technological level (or nearly our technological level). Conequently, because the Milky Way is at least 10 billion years old, there has been plenty of time for civilizations to explore the Milky Way galaxy. The Fermi Paradox then posits that if this is indeed true, then why have we not found evidence of extra-terrestrial civilizations?

In the next few sections, we go through the possibilities (and strategies) for interstellar travel and exploration.

Message to M13

Off and on we try to communicate with our neighbors usually on purpose, but sometimes not. For example, in 1974 we sent a messge from the Arecibo Radio Observatory in Puerto Rico in the direction of the globular cluster M13, around 25,000 light years away. The message was a string of 1,679 bits of information, each bit was set to either 0 or 1. The message was beamed into space with power 1,000 kiloWatts tuned to a broadcast frequency of 2,380 MegaHertz. The broadcast lasted less than 3 minutes.

At right appears the decoded message. Click on the image and you will see the string of 1,679 zeroes and ones sent toward M13. How were the 1,679 zeroes and ones read to produce the image to the right? The simplest strategy is to try and interpret the one-dimensional string of zeroes and ones. If this doesn't lead anywhere, try to convert the one-dimensional string of zeroes and ones to a two-dimensional picture and so on. Given this idea, the what becomes the best strategy? Further, once we are able to produce the image to the right, how easy would it be to interpret the picture? Uhh, seems difficult. Clearly, the senders did not (may not) expect the receivers to understand the messge. The senders presumably (in my opinion) hoped that the receiver would recognize the signal as something more than noise not necessarily be able to read the message.

Inadvertent Messages

The Earth has been broadcasting to space with powers up to 500 kWatts, nearly the power of the Arecibo M13 message, for the last 50 or so years (radio and television) and so we have been announcing ourselves to the Galaxy (inadvertently announcing ourselves) for a while. However, with the advent of digital signals, the power leaked to space has gone way done and so this inadvertent CETI has essentially stopped.

Interstellar Travel

The Milky Way galaxy is large, the visible disk of stars is around 100,000 light years across (around 6x1017 miles). The nearest star to the Earth, excluding the Sun, is Proxima Centauri which is around 4.3 light years from the Earth. So, if a spacecraft could travel at the spped of light, c, it would take 4.3 light years for the ship to travel from Proxima Centauri to the Earth and it would take ~100,000 years for it to travel across the Galaxy. This simple argument would suggest that perhaps a very technically advanced civilization could easily explore the Galaxy over the lifetime of the Galaxy, > 10 billion years.

Interstellar Travel and Exploration

If the civilization is roughly like ours and uses space probes similar to ours the argument is changed. (In the left panel we show an artist's rendition of Voyager. In the right panel we show the disk carried by Voyagers 1 and 2. The Pioneer probe also carried plaque as it explored the Solar System and beyond.) For example, we live in a planetary system dominated by the Sun, our star. When we send probes into space such as the Voyagers, we try to do it in an economical way; we launch the probes just fast enough to escape the Earth and to reach their desired destinations. If we want a probe to escape the Solar System, we would give it the escape velocity from the Solar System. From the orbit of the Earth, this corresponds to a speed of ~150,000 kilometers per hour.

The Pioneer 10 and 11 probes were launched in 1972 and 1973 and have left the Solar System. We received the last signal from them on January 23, 2003. Pioneer 11 is headed in the direciton of the constellation Aquila and will pass near one of its stars in 4 million years.

In the 1970s NASA launched Voyagers 1 and 2 to tour the outer Solar System and beyond. Currently, Voyagers 1 and 2 are leaving the Solar System traveling at speeds of 3.6 Astronomical Units per year (roughly 63,000 kilometers per hour) and 3.3 Astronomical Units per year (roughly 57,000 kilometers per hour), respectively. In 40,000 years, Voyager 1 will pass within 1.6 light years of AC+79 3888 in the constellation Camelopardalis. In 296,000 years, Voyager 2 will pass witin 4.3 light years of Sirius, the brightest star in the sky.

We are already in the Process of Visiting Other Stars

It is not clear, however, how far the Pioneers and Voyagers can wander through the Galaxy before they meet their ends.

If the extraterrestrial civilization lives in a planetary system to ours and is also interested in economy, then we would expect that it would also send out probes with speeds like those of Voyagers 1 and 2, speeds on the order of 60,000 kilometers per hour or so. In this case, the trip from Proxima Centauri would take

Trip = (length of trip)/(speed) = 80,000 years

and a trip across the Galaxy would require 190 million years. Such times are both shorter than the age of the Galaxy and thus still plausible that extraterrestrials could explore the Galaxy over the lifetime of the Galaxy. From a practical standpoint, the exploration of the Galaxy is likely a multi-generational exercise. Motivation and drive will then play large roles in whether any civilization is willing to undertake such an adventure. The exploration of the Galaxy is then a psychological and sociological question as well as a simple scientific question.

Are there ways to go about exploration which remove psychological and sociological considerations?

Von Neumann Machines:

The above series shows the rate at which interstellar civlization spreads. After only 50 million years it has spread over a large chunk of the Galaxy.

Cotta and Morales (2009) performed a simple exercise. They start with a technological civilization which sends out eight probes each traveling at 10 % the speed of light. These probes carry subprobes for use to explore further. Each set of subprobes carry subprobes, and so on. That is, the probes act as von Neumann machines , machines capable of replicating themselves. The game is then, the eight probes will reach their destinations after a certain amount of time elapses. When they reach their destinations, they set up civilizations (bases) which last for N years, and then send out eight more probes. So, we see that there are now 64 probes moving outward. These sixty-four probes reach their destinations, set up bases, and each sends out eight more probes. After this stage, there are now 512 probes. This process continues until the probes die.

If the bases last 1 million years, there can be no more than 1,000 civilizations for probes which last 50 million years or we would have found evidence of extraterrestrial civilizations. If the bases last 100 million years, then there are not likely to be more than 10 extraterrestrial civilizations. Again, like the inferences drawn from the Drake Equation, conclusions based on the Fermi Paradox also depend on the assumption of key numbers and questions (implicit questions) on the motivation of technologically advanced civilizations.

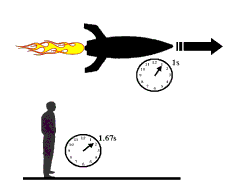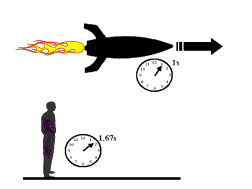High-Speed Space Travel and Special Relativity

There is a well-known upper limit to the speed to which a massive object can be accelerated. Objects with mass cannot be accelerated to the speed of light, c = 300,000 kilometers per second without an investment of an infinite amount of energy. Because of this limit on the ultimate speed of travel, there remains an upper limit of 100,000 years or so to explore our Galaxy thus not allowing LAWKI to perform a single generation (or few generational) trip to cover our Galaxy. Or does it?

There is an interesting feature of Einstein's Special Theory of Relativity which affects this issue. For a brief discussion of Special Relativity go to this link. Because of the property of spacetime that it is malleable, not rigid (which also includes the time part) time does not have to flow at the same rate for all observers. In fact, it has been amply demonstrated by experiment that moving clocks run more slowly than stationary clocks! The rate at which a moving clock runs is given by the formula to the right. For the rider on the rocket (see left panel), let's say his watch reads that t = 10 hours have elapsed. If the rocket is traveling at speed v = 0.9 c, then, amazingly, it turns out that the watcher (on the ground) would find that his clock would read that roughly t' = 23 hours elapsed over the same time interval.

Twin Paradox

There is an interesting consequence of time dilation . Imagine two twins, one stays on the Earth while the second travels to Proxima Centauri (on a ship traveling at 90 % of the speed of light). After reaching Proxima Centauri, the traveling twin immediately turns around and returns to the Earth. Because Proxima Centauri is 4.3 light years from the Earth, the stay-at-home twin sees the trip take 9.6 years. Interestingly, the traveling twin finds that the trip, according to his watch takes only 4.0 years. The closer the traveler gets to the speed of light, the less he will have aged.

But wait, according to Einstein, time dilation says that, according to a stationary observer, a moving clock runs more slowly than the stationary clock. This fits nicely so far as it suggests that the traveling twin's clock does indeed tick more slowly than the stay-at-home twin. The paradox arises because all that is really needed is that two observers are in relative motion for time dilation to occur. So, if we were to consider the situation from the point of view of the traveling twin, we would come to a different conclusion. The traveling twin sees the stay-at-home twin running away from him as he speeds toward Proxima Centauri, that is, he believes that the stay-at-home twin is the one who was in motion. Consequently, he believes that the stay-at-home twin's clock is the one that ran more slowly and he is surprised when they re-unite and the stay-at-home twin has actually aged more. This is the Twin Paradox. For an explanation of the paradox see here.

Fast, Long-Distance Traveling and General Relativity: Wormholes

Let us set the stage for a moment. How do we describe the location of events which occur in the Universe? Is it sufficient to give simply the where of the event? No, in order to define uniquely the event, we must also say when the event takes place. That is, if we want to define events in our Universe we must give the location and time of the event. In this sense, time acts as just another coordinate in the Universe much as we define the x,y,z positions for objects in space. This, however, immediately points out that time, although apparently just another coordinate for Universal events, seems to have special properties--we return to the specialness of time later. Space and time form a structure, spacetime, on which (in which) events in the Universe take place. But his also begs the question of whether space and time are things or mathematical constructs.

Issac Newton and the Clockwork Universe

In Philosophiae Naturalis Principia Mathematica (1687), Newton gave his three laws of motion which laid out a prescription for how motions marched forward in time, to the future, in our Universe, given conditions of today. Newton after due consideration, decided space was the rigid framework within which events took place, and considered time as a smoothly (and uniformly) flowing quantity which was the same for all observers in the Universe. Time was simply kept by a Universal clock which inexorably marched forward uniformly and at the same rate for all observers. The Newtonian theory and these notions for space and time work nicely for normal daily events (such as placing astronauts on the Moon) and are perfectly valid for most commonplace situations. (They do breakdown under certain conditions, high speeds, small scales, and/or low energies which we address later.)

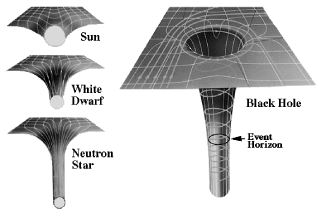Albert Einstein and Spacetime

Einstein relaxed the conditions of fixed space and time; he considered non-rigid space and stretchy-squishy time in his famous theories of relativity (the theories of Special Relativity and General Relativity). A notion contained in his General Theory was that of the nature of gravity. Newton postulated a Universal Law of Gravitation, but did not understand how gravity worked. Einstein postulated that effects of gravity arose because of the non-rigid nature of space. Mass distorts the structure of space. In a two-dimensional space, situations such as shown to the left may arise. The black hole actually pinches down to a point (the singularity) surrounded by something called the event horizon. Once the event horizon is crossed you can no longer communicate with the rest of the universe.

Wormhole

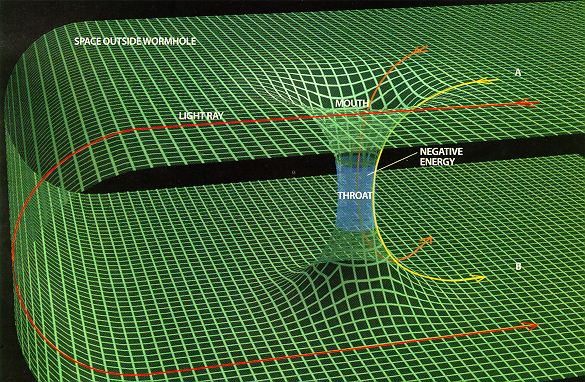A black hole is surrounded by an event horizon which is a one-way gate into its insides. Interestingly, can also envision a solution where time is reversed so that one can make a white hole surrounded by a horizon, also a one-way gate, but everything flows outward. Hooking up two such beasts forms what is known as an Einstein-Rosen bridge, an example of a wormhole. Such objects are unstable in the presence of ordinary matter. As one tries to traverse the wormhole, the pinching in of the throat compresses the material increasing its gravitational pull of the walls of the wormhole further compressing it. This can be overcome if an AAC was around. Material which acted as if it had negative mass could be manufactured which would serve as a repulsive force to keep the throat of the wormhole open as the material passed through! Conceivable but whether it is likely or not is questionable.

Return to Home Page