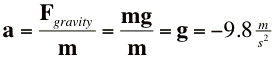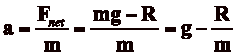Essentials of Physics-- PHYS101: Lecture 5

Essentials of Physics- PHYS 101

Lecture 5

Problem-solving tricks and techniques

Problems solving problems?

1) You can always multiply by 1

Example: 1.6 km = 1 mile. 1.6 km / 1 mile = 1. To convert miles to km, I multiply by 1:

8.0 miles x (1.6 km / 1 mile) = 12.2 km

2) Multiply both sides of an equation by the same thing (number):

Say we know that SF = m a

Say we also know a and SF. How do I solve for m?

Multiply both sides of equation, above by the same thing (1/a):

SF (1/a) = m a (1/a) => m = SF/a

More on the relationship between a, m, and F

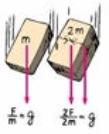
Last week we observed that the acceleration of a cart doubled when the force pulling it was doubled. More generally we found that acceleration is proportional to the net force.

a µ F

What about mass?

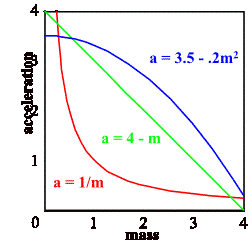We know mass gives an object inertia which resists a change in motion. Another way to say this is more mass makes an object harder to accelerate.

What is the exact relationship between acceleration and mass?

In lab you kept the pulling force constant but changed the mass of the car. What you found (hopefully) was that if the mass of the car doubled the acceleration was reduced by half.

a µ 1/m

'acceleration is inversely proportional to mass'

put all this together to get-- Newton's Second Law

Put this together with a µ F and what do we get?

a = F_net/m more commonly written as: F_net = ma !

But Dean, I checked F = ma in lab and it didn't work!

How does gravity work?

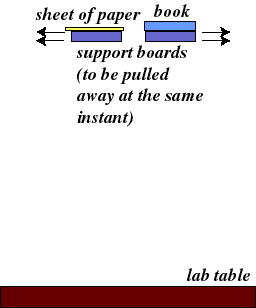
Let's observe the effect of "gravity" on a softball with the following experimental setup: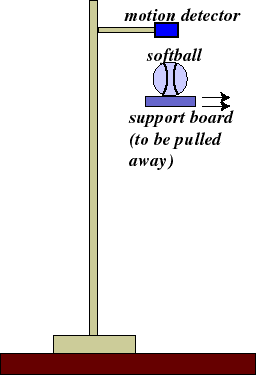

Question: What happens when the board is pulled out from under the softball?

Answer: Duh, let me guess.....

Question: So, HOW is the ball moving towards the ground?

Time for an Interactive Lecture Demonstration

Question: If the ball is accelerating, what is causing the acceleration?

Answer: The "force of gravity," the attraction between the Earth and the softball, is causing the ball to accelerate downwards.

Question: Is the "force of gravity" the same for lighter or heavier (less or more massive) objects of a similar shape?

Try this experiment:

Answer: OK, so they both hit at the same time (after suitable modification). That means that they both accelerated in an identical manner, speeding up towards the table at the same rate.

The Force of Gravity

or

Sir Isaac Newton to the rescue!

The gravitational force that the earth exerts on an object is proportional to the object's mass.

So in free fall an object's acceleration is:

Not-so-Free Fall

or

Was Aristotle some kind of idiot or what?

What is our every day experience with falling things?

Take paper for instance:

Terminal Velocity (no not the movie with Charlie Sheen)

Air resistance (unlike friction) depends on the velocity of an object. As the speed of a falling object increases, the resistance force increases until it exactly balances the weight of the object. When this happens the net force will be zero and the object falls with a constant velocity called its terminal velocity.

Imagine putting your hand out the window of a car as it accelerates. Certainly the faster the car goes the more force the air exerts on your hand. This is because air resistance is proportional to velocity.

We can write it as, R = bv, where b is a number that depends on the how much air an object has to move through (something to do with its shape).

Terminal Velocity is reached when F_net = 0 ( or W - R = 0 )

Another way to state this condition is mg - bv = 0

This lets us see that the Terminal Velocity is

So Aristotle wasn't really so dumb. Massive things do fall to earth faster when air resistance is important!