Physics of Energy & the Environment- PHYS 161

Lecture 13

Reading: Chapter 8, pages 132-141.

Homework: HW #3 is due Thursday (11-Nov.) in class.

Heat and Temperature

First Law of Thermodynamics

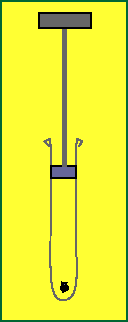
This is just a statement of energy conservation in disguise. In fact, this is the most general statement of energy conservation one can make.

What is Internal Energy?

One way to quantify internal energy is to measure a system's temperature. Some times, however, the internal energy increases via phase changes, where ice goes to liquid water, or liquid water turns into vapor. In both cases the storage of internal energy involves chemical bonds that are vibrating or being broken.

Mechanisms for Heat Energy Transfer

Heat energy can be transfered by three different mechanisms:

An example-- Energy conservation in the home

    To better understand the three mechanisms for heat energy transfer, imagine you were charged with doing things to lower the heating bill (weatherize) an ancient cathedral in Bath, England.

  1. The first thing you should do is repair all those fancy windows and doors. They are a source for drafts (not the game played in pubs), where warm air leaks to the outside and is replaced by cold air from outside. This is heat energy by convection, because warm air is moving, taking heat energy with it. Studies show that cutting down air leakage is the most cost-effective form of weatherization.
  2. The next thing to consider is insulating the ceilings, walls and floors of the cathedral. Insulation cuts down on heat energy transfer out of the building via conduction. As warm air typically accumulates near the ceiling (why is that?), a greater difference in temperature exists between the ceiling and outdoors than elsewhere in the building. That is the place to start adding insulation.
  3. After you have caulked (cut drafts) and insulated ye ole cathedral, its time to think of extreme measures. For example, you might want to paint the outside of the cathedral black so that it better absorbs heat energy from the sun. Why is this extreme? Well, it really is the least cost-effective thing you can do. Heat loss or gain by radiation is usually a small factor affecting a building heat budget. Besides, whether this helps or not really depends on the temperature outdoors. During summer you may end up overheating the cathedral. And then where would they sing evensong?

To get a perspective on how the energy used to heat buildings compares to other forms of energy use in the US, let's look at table 24.3 from your textbook:

Use
Percent of US Fuel Consumption
 Second-Law Efficiency (%)
Space heat
      18
      6
Process steam
      17
      25
Auto transport
      13
      10
Truck transport
      5
      10
Water heat
      4
      3
Air conditioning
      2.5
      5
Refrigeration
      2
      4

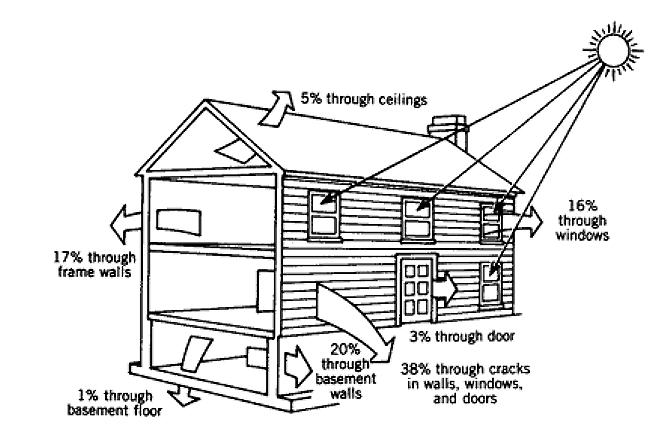
Evidently space heating represents a substantial part of the US energy budget!

All that aside, conservation of a building's thermal energy can be thought of as another energy source. Because a weatherized building uses less energy for heating, that saved energy can be used elsewhere. Conservation of thermal and other forms of energy has an added benefit. Compared to the second-law efficiencies of various energy conversion processes (we'll get to that next lecture), energy conservation is 100% efficient!

For more information about heat transfer mechanisms and weatherizing a home, see Prof. Bothun's page on insulation in the home.

We can do a simple calculation to estimate the yearly energy savings when insulating a house. Insulating a house involves cutting heat energy loss by conduction. The rate at which heat flows through a system boundary (Q) is given by:

where k is the thermal conductivity, A is the area of the boundary (say the wall of a house), DT is the temperature difference across the boundary, and t is time.

We can restate this rule in more common units of thermal resistance, R, as:

The "R-value" of insulation is typically written on home insulating materials and, in the US, assumes units of square feet and temperature differences in degrees Farenheidt. Its US units are {hr ft2 oF / BTU} (note the hour).

For a home with a given R-value for walls, ceilings and floor, and a fixed area for heat energy transfer, a greater difference in temperature (DT) results in a greater heat flow rate. The average daily difference between the temperature outdoors and an assumed indoors temperature of 65 oF is called a degree-day.

Degree-days are compiled for various locations around the US and abroad. For example, the degree-days for Eugene are approximately 4,200.

Question: If the Eugene heating season is 150 days long, what is the average daily outdoor temperature?

So degree-days are a convenient way of stating both temperature difference and time. To calculate heat loss by conduction using degree-days, we write:

(The hour/day conversion converts degree-days to degree-hours, so as to cancel with the hours in the units of R.)

Specific Heat:

If we transfer the same amount of heat energy into two different kinds of material, say equal masses of steel and aluminum at identical temperatures, will their temperature increase be the same? Why or why not?

Conversely, if we have equal masses of steel and aluminum at the same initial temperature and we transfer heat from them until they are at the same final temperature, will the amount of heat energy transfered be the same?

The heat capacity of an object is the ratio of the amount of heat transferred to an object to the rise in temperature of an object. If you know how much heat energy you have transferred to an object in joules, and the heat capacity (or its specific heat), you can predict how much temperature change the object will undergo. This is expressed as:

Let's examine a table giving the specific heat's of different substances. Water has a very high specific heat, which is fortunate for us. Because water's heat capacity is large, it doesn't change temperature much upon absorbing large amounts of heat energy from the sun when compared to the temperature change predicted for air. {By the way, the "p" in cp stands for constant pressure, meaning that value is good if the heat energy is absorbed by the object at constant pressure.}

The oceans, then, are very good at storing thermal (internal) energy. Why? The specific heat of water is very high, and they can absorb heat from the sun without undergoing large changes in temperature (which would serve to cool them down faster). If we transfer enough heat energy into 1kg of air (which occupies about 1 cubic meter of volume) we can raise its temperature 1 degree C (or K, same difference). If we turn around and transfer that same amount of heat energy into 1kg of water, we will raise its temperature about 1/4 degree C. Thus we have stored the same amount of heat (in considerably less volume, about 1/1000 the volume of 1kg of air) with 1/4 degree temperature change. Although the temperature of oceans near the equator aren't much higher than night-time air temperature (on the average), the amount of heat available for transfer from the oceans is HUGE! That's why we have hurricanes!

Heat Engines are Everywhere.... Arrgh!

Heat engines play a crucial role in our technological society. They propel cars, trucks, motorcycles, trains and airplanes, and they are used to generate electricity at coal- and gas-fired power generating facilities. Heat engines exist in nature as well.... in fact weather systems that transport thermal energy from equatorial regions can be though of as planetary-scale heat engines.

So what is a heat engine and why don't we hear more about them in every day life?

Definition of a heat engine:

Any device (or planet, hee hee) that exploits a temperature difference to perform work.

When two systems at different temperatures are placed in contact with one another, heat energy transfer will take place between them. If left alone these systems would eventually reach thermal equilibrium with one another. A heat engine converts some of the heat energy that is transferred into useful work.

Characteristics that define a heat engine?

1) "A heat engine exploits a temperature difference......"

2) "..... to do work."

3) Human-devised and naturally-occuring heat engines function cyclically.

4) Energy is conserved within the entire closed system-- heat source, engine and heat sink.

5) Some heat energy must ALWAYS be transferred to the heat sink. The engine can NOT be 100% efficient.

So the first thing we need for a heat engine to work is two systems, or reservoirs, at different temperatures. For example, the hot gas resulting from combustion of the gasoline vapor/air mixture fed into your automobile's engine has a higher temperature than the water in the cooling system. The hot gas can be called the heat source and the water in the cooling system the heat sink. The maximum amount of work that can be performed by the heat engine is the difference between heat out of the source and heat flowing into the heat sink.

Diagramatically we can represent a heat engine as follows:

The function of a heat engine is analogous to the conversion of the gravitational potential energy of water stored behind a hydroelectric dam into electrical energy. In order to "generate" hydroelectricity we need an upper reservoir (behind the dam) and a lower reservoir, which may simply be a stream or river. There must be a place at lower elevation (a "heat sink") where the water can go in order to extract work (in the form of electrical energy) from the upper reservoir. Just as one can't imagine generating electricity within the reservoir of water behind a dam, work can not be extracted from a heat engine without a second reservoir at a lower temperature. This principle is summarized in the second law of thermodynamics, which states:

It is impossible for a machine (heat engine) to take heat energy from a reservoir at a certain temperature, to produce work, and to exhaust heat to a reservoir at the same temperature.

Remember our "molecular model" view of nature, where gas molecules are moving with some average velocity. In our fire syringe, gas molecules gained internal energy (kinetic energy) only when they collided with the moving plunger. The rest of the time they are bouncing around the syringe in a random fashion (neglecting conduction of heat energy through the other 3 sides of the cylinder).

Now imagine doing work on the plunger. The air molecules inside must be warmer than their surroundings to extract work from the system. Otherwise, equal-temperature air molecules on the outside would be pushing back on the plunger and it wouldn't move. So the more active molecules on the inside "win" and push the plunger to the left, doing work on the environment. Even if the other three sides of the syringe are perfectly insulated, however, some of the heat energy transferred to the environment will "escape" being turned into work-- again because the plunger and outside air will absorb some heat energy. So we can state the Second Law of Thermodynamics in a stronger form:

It is not possible to extract heat energy from a reservoir and perform work without rejecting some heat energy to another, lower temperature reservoir.

Efficiency of Heat Engines

We define the efficiency of a heat engine as the ratio of the work done by the engine to the heat energy transferred from the heat source:

Because, with no change of internal energy over a cycle, the work done equals the difference between the heat energy transferred in from the heat source and the heat transferred to the heat sink. Efficiency can be written symbollically as:

One would multiply this number times 100 to get efficiency in percent. To improve the efficiency of a heat engine, as defined above, one must increase the energy transfer from the heat source (by increasing its temperature) and/or decrease the energy transfer to the heat sink.

A certain type of "perfect" heat engine follows the Carnot cycle, where heat energy transfer and work extraction are done such that the process is reversible at every step. This Carnot engine is an idealization, but serves to place an upper limit on the efficiency of "real-world" heat engines. The efficiency of a Carnot engine is given by:

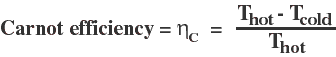
Note that the efficiency of a perfect heat engine, following a Carnot cycle, is always less than 100%. This is another way of stating the Second Law of Thermodynamics-- Even the (unrealizable) perfect heat engine can't be 100% efficient. All of the heat energy transfered from a hot reservoir will not be converted into useful work.

Real heat engines involve losses to friction, among other things. When energy is lost to friction, it is irrecoverable. Thus the real heat engine is less efficient that the Carnot cycle engine.

The average automobile (heat) engine operates at a temperature of about 3300K, exhausting its spent fuel at 1400K. Its Carnot effiency is then:

Because the exhaust gases of an automobile are very hot relative to outdoors, more heat energy is lost in this process that what is accounted for above. That, combined with friction losses, reduces the efficiency of an automobile engine to about 25%.

The following table (excerpted from Physics, by Hecht) gives some approximate (and real) efficiencies of various devices:

Previous Lecture Next Lecture Back to Course Page.