Reading: Chapter 3, pages 26-29.

Recap on Motion

Forces

Gravity

The Ubiquitous Automobile

Definitions in Words

Recap on Position, Velocity and Acceleration.

• Acceleration? We defined it to be related to velocity vs. time.

• 

  Definition: average acceleration is the change in velocity over the time elapsed.

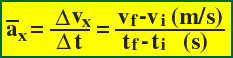
Using the motion detector and graphing software, try moving to match an acceleration vs. time graph. Is it simpler to match a velocity-time graph, like above?

Note that we should usually be very careful when describing the motion of an object. The expression above relates acceleration in one dimension (x) to the velocity (speed, really) in that direction and time. To fully describe the motion of real-world objects, we need to keep track of motion (positions, velocities and acceleration) in all three dimensions. If we aren't careful about this, it will come back (soon!) to haunt us.

So we really have just succeeded in carefully defining some (physics) variables that help describe our system (an object in motion). Big deal! Things become more interesting when forces are applied to them.

Let the Force be with You...

The fan attachment exerts an almost constant force on the cart. What is the relationship between that strength of that force and the cart's acceleration?

We know about position, velocity and acceleration. Obviously, (strength of) force is another consideration. Are there any other important variables?

Time for an Interactive Lecture Demonstration (ILD):

Hypothesis I: acceleration is proportional to total force (for constant mass).

• 

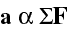
Experiment I: test hypothesis I. How do we do this?

What about when we vary mass?

Hypothesis II: acceleration is inversely proportion to mass (when force is held constant).

• 

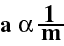
Experiment II: test hypothesis II. How do we do this?

Result: Hypotheses I and II are correct. They can be summarized as Newton's Second Law:

• 

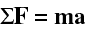
An important postulate to this is Newton's First Law:

If the sum of the forces on an object is zero, it is not accelerating. Hence, if an object is in motion and the sum of forces on it are zero, it will stay in motion (maintain a constant velocity).

What is "gravity?"

Let's observe the effect of "gravity" on a softball with the following experimental setup: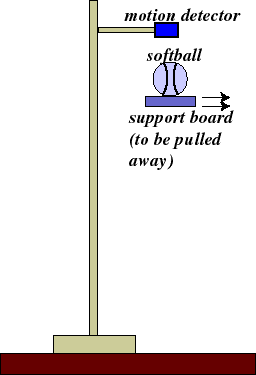

Question: What happens when the board is pulled out from under the softball?

Answer: Duh, let me guess.....

Question: So, HOW is the ball moving towards the ground?

Answer: The ball is accelerating towards the ground, as we observe its velocity to be changing at a constant rate over time.

Question: If the ball is accelerating, what is causing the acceleration?

Answer: The "force of gravity," the attraction between the Earth and the softball, is causing the ball to accelerate downwards.

Question: Is the "force of gravity" the same for lighter or heavier (less or more massive) objects of a similar shape?

Try this experiment: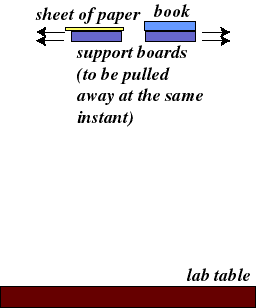

Answer: OK, so they both hit at the same time (after suitable modification). That means that they both accelerated in an identical manner, speeding up towards the table at the same rate. By Newton's II Law, the force of gravity acting on them is NOT the same. It varies in just the right way, according to their mass, so that they have the same acceleration.

The Ubiquitous Automobile

Let's take a look at the forces exerted on a motor vehicle by its environment. Those forces are:

If the vehicle is maintaining a constant velocity, then by Newton's first law the sum of the forces on it is zero. Then the motive force, exerted by the engine on the car, is equal in magnitude to all those other forces combined.

Limits on the first two forces on the right are determined by engine size. They represent the extra force necessary to either accelerate the car from standing still, or to push it up a hill.

During normal operation (relatively low speeds), the rolling force is the largest of the four. As a car goes down the road, its tires are constantly deforming as they roll. Overcoming this rolling resistance requires effort from the car's engine.

The last term is the force of air on a moving car. The car must displace air out of its way as it travels. For a given car, this term depends both on the cars drag coefficient (how far the air must move to get out of the way) and the car's speed. The "aerodrag" force increases linearly with the coefficient of drag. It increases with the velocity of the car squared. The latter means the engine of a car moving at twice the speed must exert four times the force.

Definitions for speed, velocity, acceleration, force and mass in words.

• Average speed of an object during a given time interval is the change in its position divided by the length of that time interval.
• Average velocity is the change in position (or displacement) divided by the change in time (or time elapsed).
• Displacement, velocity, acceleration and force all have magnitudes and directions.
• Acceleration is a measurement of both the change in speed and the change in direction of an object. Average acceleration is the change in velocity divided by the time interval.
• Experiments show that the acceleration of an object is directly proportional to the net force acting on it. This has several ramifications:
  • As the net force applied on an object is increased, so is the object's acceleration. If the acceleration of an object is observed to decrease, then the net force acting on it must also have decreased in magnitude.
  • The direction of the acceleration is the same as the direction of the net force.
  • If no net force is exerted on an object, then its acceleration is zero (does this mean it velocity is necessarily zero?).
• Experiments also show that, for a given net force acting on an object, the acceleration of the object is inversely proportional to its mass.
  • Thus, if the mass of an object is decreased, its acceleration will increase.
  • Mass in this context is sometimes called inertia-- its resistant to change in motion. An object with greater inertia will resist change in motion (specifically, it will accelerate less) than a less massive object, all other things being equal.
• These two observations taken together can be summed up as Newton's Second Law: The acceleration of an object is proportional to the net force acting on it, and the constant of proportionality is the object's mass.

Previous Lecture Next Lecture Back to Course Page.