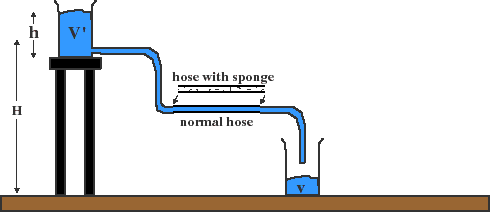
Efficiency in transport of people is quantified by the energy cost per "passenger km" (or passenger mile in U.S.). For example, the energy cost of the bicycle is 130 kJ/passenger km (kJ stands for 1000 Joules). For walking it is 200 kJ/passenger km. The lower the energy cost, the more efficient the transportation.
The energy cost states the maximum efficiency attainable. The "load factor" gives the percentage of that maximum that is typically attained. For example, if your car is rated at 2000 kJ/passenger km for a full load of 4 adults, and you and your friend drive across town, your load factor is 50%. The energy cost of your driving across town is:
If you and your friend drive the 10km across town your total energy consumption per passenger is:
If you and three friends drive across town, the consumption is:
The contribution mass transit (buses, subways, etc.) makes towards conserving energy in transportation depends on the average load factor of the bus or subway train.
{worked example similar to Aubrecht}
and what if 10% of us commuted by bicycle?
Obviously, raising the corporate average fuel economy (CAFE) for passenger cars is a good thing. The rewards for this are:
We (U.S.) currently import over 60% of the petroleum we consume. Take away cars, and we would import little to no petroleum.
Every 1 mile/gallon improvement leads to a reduction of 0.0229 g/mile x 12,000 miles/year x 200,000,000 cars = 5,500 metric tons of hydrocarbon emissions. And I just guessed that there are 200 million cars in the U.S., there are probably more.
![]()
How do we increase fuel economy without increasing pollution? The three most effective measures are:
That means get out of those "sport utes," which are relatively heavy and have greater air resistance (higher off the ground)!
The federal government has in place a set of standards for fleet mileage (CAFE). It has been reinstated for passenger cars, but currently sport utes and mini-vans, which are classified as light trucks, are exempt from both fleet mileage goals and emission standards.
It may seem to be an obvious thing to put those types of vehicles up for CAFE standards, but remember that 8.5% of our total economy relies on selling automobiles. Mandating that high profit sport utes and minivans meet CAFE standards might put a dent in our humming economy (oh no!).

Well this seems to be a no-brainer. Trucks require about 10 times as much energy to transport a ton of load per km as do railroads. However, freight railroads pay their own way for construction and maintenance of track. Trucks pay only about 76% of their incurred costs (as of 1995.) The Oregon chapter of the AAA (American Automobile Association) claims that the gas tax restructuring, recently passed by the Oregon legislature, actually shifts road construction and maintenance costs from the trucker to the automobile driver. Hmmm. If the AAA is correct, it doesn't seem that transport-inefficient trucks need further subsidy.

Electricity is about charge. Charge is a property of electrons and protons. Negatively-charged electrons can be mobile because they have 1/1830 of the mass of the positive proton. Neutrons have the same mass as a proton, but no charge:

Protons are the original homebodies. They are NOT easily removed from a nucleus and do NOT constitute the positive charges that we see in physics class.
Instead, "holes" are the name physicists give to missing electrons. They are mobile like electrons and have positive charge.

Charge comes in bundles of specific size, as the proton's charge is the same as the electron's (but with opposite sign). The size of this bundle is called a quantum of charge. Charge comes in bundles that are indivisible.... one can have a charge of +1, +2, +3, etc, but not of 1/2 or 1/3. Charge is measured in Coulombs (C).
An object with -1 coulombs of charge has a net surplus of 6 x 10^18 electrons!
![]()
1) Forces between like charges: Take two pieces of scotch tape. Stick them to a table along most of their length. Rip each piece off the table. You have just charged each piece in the same way with the same type of charge. Holding them by their ends, bring them near each other. What happens? Why?
2) Forces between unlike charges: Charge a metal coated pith ball by rubbing a black rubber rod on fur. That makes the rod negative (excess electrons). Touching it to the pith ball allows some of the charges to escape to the pith ball. (Why?) Now charge a lucite (clear) rod by rubbing it on silk and hold it near the negatively-charged pith ball. What happens? The lucite rod is charged positively. What "rule" can you make after observing this phenomenon?

3) Polarization: Again charge the black rod negatively. Bring it near an uncharged pith ball. What happens first? What happens after the ball and rod touch? Can you describe the charge distribution on the pith ball before they touch? If so, why is the ball attracted to the rod?
Summary: The results of these simple experiments reinforce the ideas that like charges repel, unlike charges attract, and that the electric force between charge diminishes with distance.
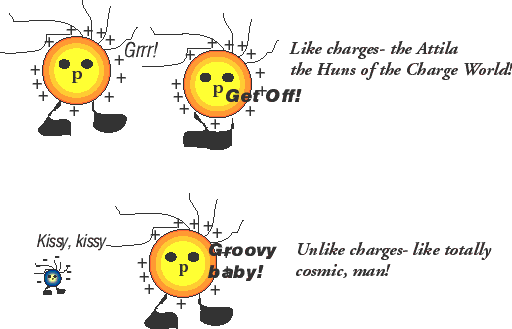
In saying that the charged rods/pith balls repel or attract, we really mean that they exert forces on one another. The negative charge on the metal surface of the pith ball is attracted to the positively-charged glass rod. It moves as close as it can get to it.
Experimentation shows that the force between two charged objects is proportional to the charge on each object and weakens according to the square of the distance separating the charged objects:
In this case, "q" is the standard symbol that means "amount of charge (in Coulombs, usually). The separation is typically stated in meters (m). The constant for these units is:
For two objects with given charges q_1 and q_2, the force between them will diminish by 1/4 if the separation between the objects is doubled.
It turns out that this is exactly analogous to the force between two masses, which we have termed "the force of gravity." For gravity, however, we almost always are referring to the attraction of an object to the Earth. As the Earth is really quite large, moving small distances above its surface has very little affect on the force (and acceleration) of gravity.
To observe the electric force in action, we can watch what happens when styrofoam balls sitting on top of a Van de Graff generator accumulate excess charge from the generator:
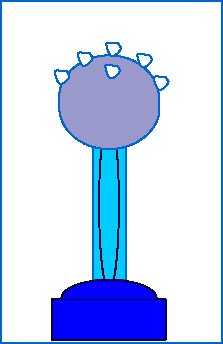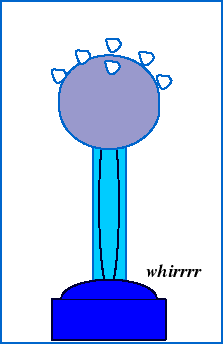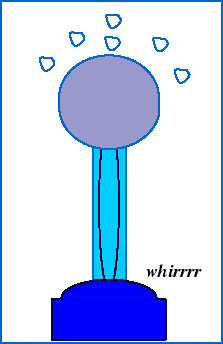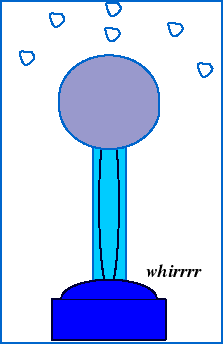
Consider two objects, each with an excess of the same type of charge. These two objects will tend to repel each other.
Our rule (tested hypothesis), above, says these two will tend to repel each other. In fact they will repel each other more (with greater force) if the charges are moved closer together.
Imagine pushing one of the "charged" objects towards the other, which is fixed and can not move. You would have to do work on the charge being pushed, exerting a force on it over a distance. If work is done on the moved object, its energy must increase. That increase is called electric potential energy. If you let go of the moved object it will want to fly away from the fixed, charged object, converting electric potential energy into kinetic energy.
For two different positions for the moved object-- one close and one further from the fixed, charged object, there would be a difference in electric potential energy.
We define voltage to be dependant upon this difference. Voltage only refers to two separate locations. For example, a "D-cell" nominally provides 1.5 volts between its positive and negative terminals. It doesn't make any sense to refer to the voltage at a single location.
We further define voltage as a difference in potential energies divided by charge:
Our battery voltage source rating tells us how much work it can do on one unit of charge. Think of voltage as the push or pull that causes charges to accelerate from one side of the voltage source towards the other.
A more technical description says that "a volt is the potential difference necessary to change the energy of 1C (coulomb) of charge by 1J (joule) in moving the charge between two points." (source of quotation: Energy, by G Aubrecht, 1995, Prentice-Hall)
When like charges undergo a net motion in some specific direction-- e.g., electrons travel along a wire-- a current is said to be flowing.
All electrical appliances-- including light bulbs, stereos and televisions, electric heaters and golf carts-- require current flow in order to function. Electric current is measured in units of amperes, defined as:
Electrons in motion comprise the electric currents we use every day. In most metals the nuclei of atoms (protons & neutrons) are bonded together and many of their electrons are relatively free to move around. This is why metals are used manufacture wire. Placing a potential difference (voltage) across both ends of a wire causes the "free electrons" to accelerate along the wire.
When one connects a battery to a wire current flows, resulting in the same number of electrons coming out one end as are put into the other. In a sense, the electrons in motion form a closed loop. Indeed, a closed loop or continuous pathway is required for current to flow in a wire. Our term for this continuous pathway for current flow is a circuit.
An idealized voltage source (battery or power plant) is assumed to be an infinite resevoir of charge (electrons). The voltage source does work on the electrons to move them, increasing the electron's kinetic energy. When the electrons travel they can do work on other things, giving up their energy gained from the voltage source.
If you could somehow see microscopically inside the filament of a light bulb carrying electric current, you would see electrons accelerating in the direction of current flow. They would occasionally run into the atoms making up the filament, and would be scattered like one pool ball hitting another.
This scattering of electrons would be reducing their energy and transferring it to the atoms of the filament. The atoms of the filament would vibrate from the collision. Some of this energy of vibration would go towards making light. Most would be lost as heat transfer to the surroundings.
Electrons colliding with atoms amounts to a resistance to their passage through a material.
As mentioned before, most metals are good conductors of electricity (electrons), so they resist the flow of electrons less than other materials and are used to manufacture pathways for electron flows-- wires. Other materials, e.g. most plastics, ceramics and rubber products are highly resistant to electrons passing through them. These materials are used to clad wires, preventing the electrons from leaking out of the wire or jumping to another wire.
One analogue for voltage, current flow and resistance is show below:
The green part of this analogy shows a way to visualize what happens as electrons pass through conducting materials. Marbles on the top have more gravitational potential energy than do those at the bottom. Hence, they roll down the slanted surface. This is analgous with the case of electrons in a wire connected to a battery, which gain electrical potential energy in the battery and "roll" through the wire.
As the marbles roll down, they collide with some of the posts, and lose energy to the posts. The posts vibrate from the collisions. This is analgous to electrons colliding with atoms in a material, losing energy to the atoms, and heating the atoms as a result. The filament of an incandescent heats up following this analogy, and the result is light emission as the atoms cease to vibrate (before the next electron-atom collision).
A material that has more resistance to the flow of electrons can be thought of as having more posts per area of material. Wires, which have low resistance to electricity (and are called good conductors) have fewer "posts."
The above analogy falls short in that you might imagine that the marbles would travel faster in the feeder trays (wires) than in the resistive material (light bulb element). In the case of electricity, the current is the same everywhere in the wire, which means that the same number of electrons are crossing per second at each location along the path. In real circuits, the resistive circuit elements cause traffic jams which propogate backwards (and forwards) along the current path.
Also, don't think that the electrons coming out of one end of a wire are the same ones going in the other end, as is true for our "marble-electrons."
Another analogy for voltage, current and resistance can be seem with the "flow machine" we use for our Interactive Lecture Demonstration (ILD):