If you could somehow see microscopically inside the filament of a light bulb carrying electric current, you would see electrons accelerating in the direction of current flow. They would occasionally run into the atoms making up the filament, and would be scattered like one pool ball hitting another, much larger one.
This scattering of electrons would be reducing their energy and transferring it to the atoms of the filament. The atoms of the filament would vibrate from the collision (Joule heating). Some of this energy of vibration would go towards making light. Most would be lost as heat transfer to the surroundings.
Electrons colliding with atoms amounts to a resistance to their passage through a material.
Poor resistors (good conductors):
Good resistors (poor conductors):
One analogue for voltage, current flow and resistance is show below:
The green part of this analogy shows a way to visualize what happens as electrons pass through conducting materials. Marbles on the top have more gravitational potential energy than do those at the bottom. Hence, they roll down the slanted surface. This is analgous with the case of electrons in a wire connected to a battery, which gain electrical potential energy in the battery and are pushed through the wire.
As the marbles roll down, they collide with some of the posts, and lose energy to the posts. The posts vibrate from the collisions. This is analgous to electrons colliding with atoms in a material, losing energy to the atoms, and heating the atoms as a result.
A material that has more resistance to the flow of electrons can be thought of as having more posts per area of material. Wires, which have low resistance to electricity (and are called good conductors) have fewer "posts."
The above analogy falls short in that you might imagine that the marbles would travel faster in the feeder trays (wires) than in the resistive material (light bulb element). In the case of electricity, the current is the same everywhere in the wire, which means that the same number of electrons are crossing per second at each location along the path. In real circuits, the resistive circuit elements cause traffic jams which propogate backwards (and forwards) along the current path.
Also, don't think that the electrons coming out of one end of a wire are the same ones going in the other end, as is true for our "marble-electrons."
What, specifically, is the relationship between voltage, current and resistance of a material? Some materials behave following Ohm's law. As with the relationship between net force, mass and acceleration, we can explore the relationship by holding one of the variables constant and seeing how the other two relate.
Another qualitative analogy for voltage, current and resistance can be seem with the "flow machine" we use for our Interactive Lecture Demonstration (ILD, part B):
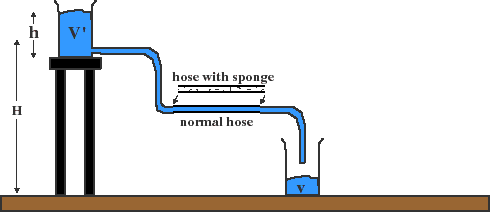
During the last lecture, we used a normal hose and a sponge-clogged hose to simulate two different resistances. We discovered that, with the sponge-clogged hose (higher "resistance") it took longer for 300ml of blue water to fall into the lower beaker (less "current"). This is analagous to less current because we define current to be amount/time. In this experiment by analogy, more resistance led to more time for the same amount.
For a fixed "voltage," then, more resistance gives less current.
If one, instead, were to use the same sponge-clogged hose each time (fix "resistance"), but raise or lower the upper reservoir level to various heights each time (vary "voltage"), the amount of water flowing per unit time ("current") would vary in a manner proportionally to the upper reservoir height.
In other words, current would be proportional to voltage for a fixed resistance. This is reminiscent of the relationship between net force, acceleration and mass.
Do this experiment with real wires, resistors, and batteries and measure current and voltage. You would then see that the relationship between voltage (V), current (I) and resistance (R) is:
What will we measure if we replace our single drain hose with two? Will it take less, the same, or more time for 300ml of blue water to transfer?
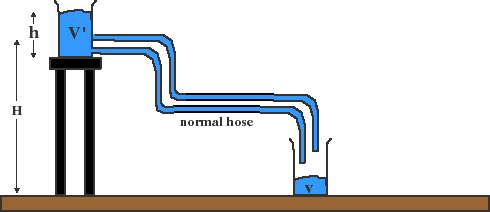
This experiment gives an analogy for parallel circuits, where electrons with the same push (voltage) have more than one path to follow. With more paths to follow and the same push as before, more current flows (300ml of blue water transfers in less time). According to Ohm's law, then, the effective resistance of the circuit is reduced. This also has implications for the power requirements of the circuit.
We defined Power as work done per unit time (units of energy in J (joules) per time (seconds). A joule per second is a watt (W).
Recall that voltage is energy/charge (units joules/coulomb) and that current is charge moving over time (units are coulombs/second). Thus voltage times current, V x I, is energy per time, or power:
Some of the power supplied to any circuit is lost as "heat," the increase in average kinetic energy of atoms and molecules of metals, air, water, pins hit by marbles, etc. In electrical circuits this process is known as "Joule heating," named after James Prescott Joule. Using Ohm's law to substitute for voltage, one can see that power is given by:
Fuses exploit this principle. If a "short" occurs in a circuit, a path for electricity to flow that has too little resistance, then current will increase through the entire circuit. As long as the fuse has the least tolerance for heat, the increased current will heat the element of the fuse until, eventually, it will melt, breaking the circuit.
![]()
Why can magnets pick up nails and paper clips? We now know that, in certain materials, a magnetic field (the lines of force surrounding a magnet) will affect the orbits of electrons circling the nuclei of atoms. The effect of orbit alignment causes the nail or paper clip to become temporarily magnetized, and it will be attracted to the permanent magnet.
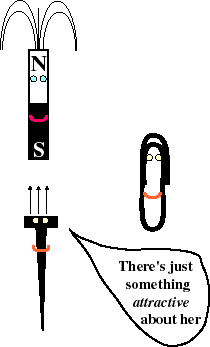
Magnetic field lines are a way to show the direction and strength of magnetic forces. The direction of the field line shows the direction of push or pull that a magnetized particle would have. The density of field lines indicates the strength of the field.
Christian Orsted observed in 1819 that a wire carrying a current (charge in motion) produces a magnetic field. This is how electromagnets work- current flows through a coil of wire, the optimal arrangement of wire for producing a strong magnetic field. One can observe current producing a magnetic field by placing a compass next to a wire carrying current:
One can reinforce the current-carrying wires magnetic field by winding it into a coil. This gives a stronger magnetic field. The field lines from this coil resemble those of a bar magnet.
So, if a current can exert a magnetic force on materials that magnets attract, can a magnet somehow interact with a current? The answer is yes, as demonstrated by our experiments with moving magnets and coils. If a magnet is moved near a coil, or vice versa, we observe that a current is produced in the coil, which lights lamps or moves a current meter. This is precisely how electric power is generated (converted, really) by electric utilities at dams, coal-fired plants, etc.
We can further refine our observations about magnets and currents by trying the following experiments:
1) Hold the magnet still inside the coil. Is current produced as evinced by the lamp or meter? NO, the magnet and, hence, the magnetic field surrounding it must be in motion relative to the coil. In fact, the faster the magnet moves, the higher the voltage produced.
- Question: Do you think that a larger current will produce a stronger magnetic field around an electromagnet?
2) Move the magnet into the coil and observe the current meter. Now pull it out again and watch. What can be said about the direction of current flow vs. the direction of motion?
Note: What you are observing is NOT due to different charges in motion. The moving magnetic field alway causes electrons to "flow" in the wire, not protons or some other type of charge.
3) Now flip the magnet end for end. What does that do to the magnetic field surrounding it? What happens now when you push the magnet into the coil and then pull it out?
4) What happens when the magnet is moved in a different direction relative to the coil? Try moving the magnet across the coil instead of through it, at about the same speed as before. Is the current produced, as evinced by the lamps or the current meter, the same?
When you move a magnet back and forth through a coil, you are doing work ON the magnet (by moving it) and work ON the electrons in the wires of the coil. The work you accomplish is evinced as increased kinetic energy for the magnet itself and the the electrons in the wire. You are doing more work than is necessary to just move the magnet. Those electrons are free to expend their new-found energy in useful ways, such as by conversion into light energy via a lamp.
Magnets can exert forces on one another. One can construct a permanent magnet as shown below. The magnetic field lines connect the magnet's "south" pole to its north.
Now place a current-carrying coil of wire so that its magnetic field interacts with the permanent magnet. In general, the fields of the two magnets (permanent and coil) will try to line up with one's south pole near the other's north (and vice versa).
If we did nothing else to our prototype electric motor, it would NOT WORK! What keeps our motor spinning? We use a special switch, called a commutator, and brushes to reverse the direction of the coil's magnetic field every half-turn. Once the coil's south pole is near the permanent magnet's north, we switch the direction of the current through the coil. This reverses the coil's magnetic field. Now the coil's north field is near north of the permanent magnet, so they repel. This keeps the coil rotating.

Thus we build our motor. Things that control the useful power we get out of an electric motor are:
If, instead of running current through the coil, one rotates the coil by hand, then electricity can be "generated." The faster the coils are rotated, the higher the voltage generated. This is similar to our experience moving the magnet slowly and quickly through the coil of wire.
So here's another way to measure your "personal power rating." How much electrical power can you generate with a hand-crank generator?