Olbers's Paradox

Olbers's Paradox

There is a simple, seemingly trivial question one can ask -- Why is the night sky dark?

This question was originally posed many years ago by a series of people (Kepler, Halley → Jean de Cheseaux → Heinrich Olbers [1823]). The answer to this question is simple, but it turns out that it tells us profound things about the Universe.

Assumptions:

the Universe is unchanging and infinite in size (or at least large in the sense we define below)
stars fill the Universe uniformly
each star has the same luminosity L
the inverse square law holds, i.e., the flux of energy from a star (energy flow per second per unit area) is given by f = L / (4 π D² ). Here L is the intrinsic luminosity of the star and D is its distance from us.

Consider a shell of stars of thickness T and radius R.

How much light do we receive from this shell of stars?

The flux of energy from one star in the shell is given by

f = L / ( 4 π R² )

By inspection of the figure, if there are n stars per unit volume of the shell, then the total number of stars per shell is
N = n x volume = n x 4 π R² x T

The total amount of flux we receive from the shell is
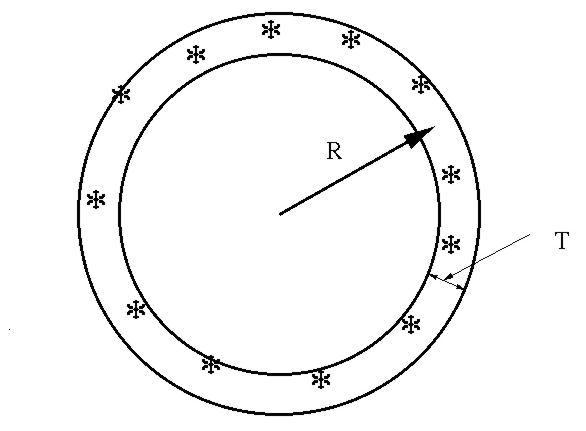
F = f x N = L x n x T
→ a simple and pretty (and interesting) result.

The key point is that the amount of light we receive from the shell does not depend upon how far away is the shell. We receive the same amount of light from distant shells as we do from nearby shells. Hmmmmmm. So, if there are million such shells in the Universe, then we simply multiply the contribution of 1 shell by million to get the total amount of energy we receive from the Universe. Further, we should see this light at all times, even at night, since the shells completely surround us. This type of reasoning gave rise to Olbers's Paradox
Another View:
Another way to think about the problem is to compare the brightness of the nightsky to the brightness of the surface of the Sun. We know that the surface of the Sun blazes away at a temperature of 5,800 Kelvin and the nightsky is substantially less bright. To understand why this is a paradox consider the following:

A star (like the Sun) of radius R_* covers an area of size,
A = π R_².
The fraction of the surface area of a sphere of radius r covered by such a star is then
fraction = π R_² / (4 π r² ) = [R/2r]².

The total fraction of the shell covered by all of the stars in the shell is the fraction due to one star x total number of stars,
[R/2r]² x [ n x 4 π r² x T ]

so that
fraction of the shell covered is ~ 5 x 10^-16 x n x T
Here, I measured the stellar density n as the number of stars per cubic parsec and the thickness of the shell in parsecs. Recall that 1 parsec = 3.26 light years. These are convenient units because in our Galaxy, there is roughly 1 star per cubic parsec and the average separation between stars is on the order of 1 parsec.

The fraction of the shell blocked out by the stars in the shell does not depend upon the radius of the shell (how far away the shell lives) → Olbers's Paradox if the Universe is big enough.

Resolution of Olbers's Paradox
Okay, so what's the way out? Something must be wrong with one (or more) of the original assumptions, or some physics has not been considered. Possibilities:

obscuration by dust → distant stars are blocked out and appear fainter. Turns out this won't work because dust, if it absorbs energy will heat up and re-radiate the energy. This means that the Universe will still be filled with the same amount of radiation, the dust acts simply as a go-between so to speak.

Expansion of the Universe 1 → redshift of photons → W(observed) is larger than W(emitted) → we absorb lower energy photons than are produced by the distant stars.
Expansion of the Universe 2 → Imagine that the star (galaxy) produces 1 photon every second. If there is no relative motion between the star and us, then we will also see photons (energy) fly by at the same rate (→ same luminosity). However, if the star is moving away from us then we will see the photons fly by a slower rate than 1 per second. This means that the energy will arrive at the Earth at a slower rate → a lower luminosity.
The preceding effects conspire to make distant objects in an expanding universe have apparent brightnesses which fall off faster than the inverse square law. This decreases the contributions from distant shells. The expanding universe effects partially explain Olbers's Paradox.
One shell of stars covers a fraction = 5 x 10^-16 x n x T of the sky. So, to make the night sky as bright as a star, we would like to make the stars cover most of the observable sky. This means that 5 x 10^-16 x n x T x number of shells ~ 1.
To calculate the number of shells, we note that there is roughly 1 star per cubic parsec in our galaxy → average distance between stars in our Galaxy (shell thickness, T) is ~ 1 parsec (explain why).
→ number of shells ~ 1 / [ 5 x 10^-16 ] ~ 2 x 10¹⁵
Because each shell is ~ 1 parsec thick → Universe needs to be at least 2 x 10¹⁵ parsecs in radius. Recall that 1 parsec = 3.3 light years and so the Universe must be at least 6.6 x 10¹⁵ light years in size in order to make the night sky as bright as the surface of the Sun.

The current Universe is ~13.7 billion years old and so has an observable size of ~13.7 billion light years. This is much less than needed to produce Olbers's Paradox. The fact that the Universe has a finite age is the principal explanation of Olbers's Paradox.

It is interesting that in asking and answering the seemingly trivial question, "Why is the night sky dark?" one could have inferred that the Universe was expanding and that the Universe had a finite age (or at the least the stars and galaxies had finite ages).

Return to Lecture 5