
|
|

|
|
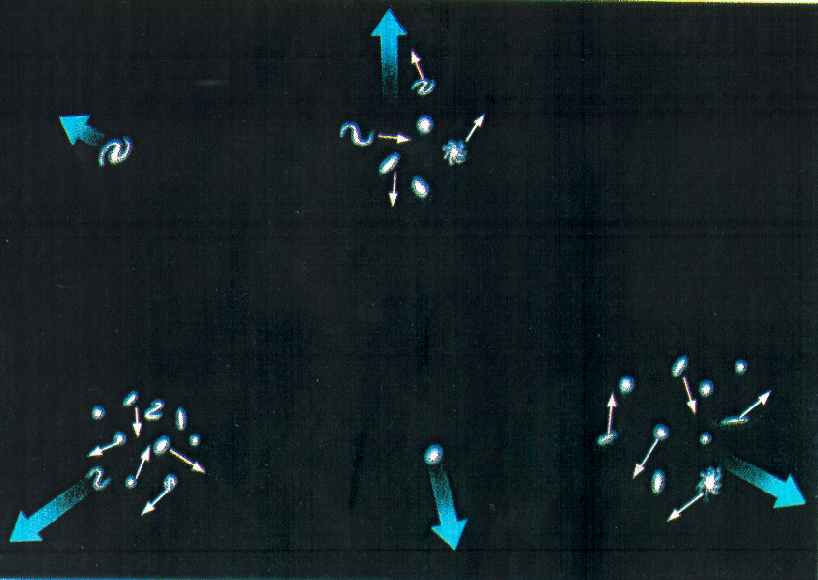
expansion velocities (Hubble flow) ===> Cosmological Redshift |

local motions (peculiar velocities) ===> Doppler Shifts |
For slow expansion speeds, z ~ v/c or v ~ cz (as is sometimes plotted when showing the Hubble law).
Recall that the relationship is linear (at least for nearby galaxies), Hubble's Law, where
The measurement of the redshifts to galaxies is straightforward and relatively easy to do. The major uncertainty in determining the Hubble relationship comes from problems in determining the distances to galaxies. We now consider this issue.
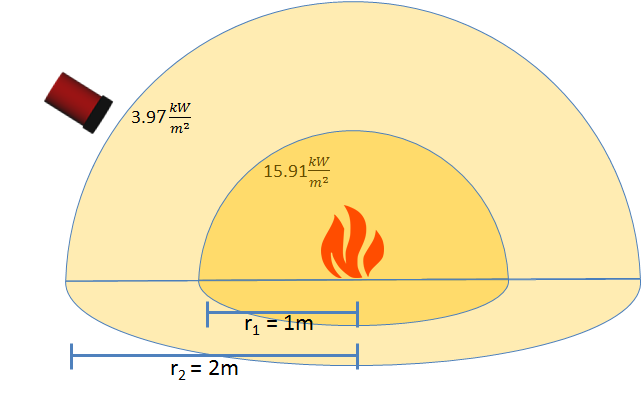
This is such an important problem that the Hubble Space Telescope (HST) made the determination of the distance scale one of its principal goals. The usual way in which distances are found is to compare the apparent brightness of an object to its true brightness. This technique relies on something known as the inverse square law and knowing the intrinsic brightness of the object that is observed.
Objects whose intrinisic brightnesses are known are referred to as standard candles.
The distance follows naturally from the observed brightness of an object from the relation:
 | 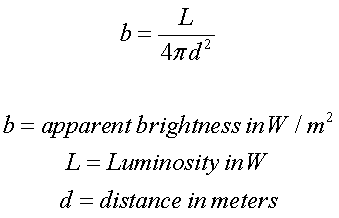
|
The inverse square law follows from the fact that the area of a sphere goes as
Area = 4πd2
where d is the radius of the sphere. The inverse square law → the distance to an object can be found by comparing its observed brightness to its intrinsic luminosity L, its true brightness.
The problem is that there is no single standard candle, an object for which we know its true brightness, which is found in systems close to us and far from us and has a large enough luminosity L to be seen at the ends of the Universe. Consequently, different standard candles must be used to find distances in different regimes. Each successively brighter standard candle is used to calibrate the next brighter one forming the Distance Ladder,
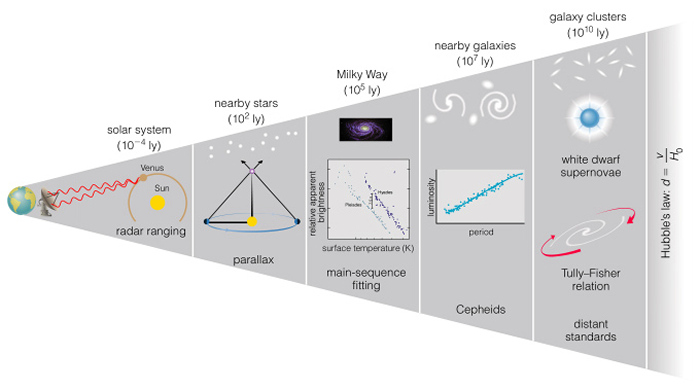
A problem with bootstrapping methods is that since each successive step is built on the previous step, the error in the method grows with each step and the method may become unreliable. Currently, there are three primary steps in the ladder, parallax, Cepheid variables, and Type Ia Supernovas (see high-z observation section).
For most extra-galactic things, people use Cepheid variable stars as standard candles for nearby galaxies as well using them to calibrate the brighter Type Ia Supernovas. Cepheid variable stars show a well-defined relationship between their periods of pulsation and their average luminosities (see here for some sample Cepheid light curves and their Period-Luminosity Relation -- luminosity versus pulsation period.) The pulsation periods of Cepheid variables correlate strongly with their average luminosities in the sense that the longer their pulsation periods, the brighter they are on average.For a novel way that HST found a distance to two Cepheids, see Hubble sees light echos from RS Pup and V838 Mon. |
Cepheid luminosities are calibrated in the first few steps of the above chain, i.e., distance to Sun (Astronomical Unit) → distances to nearby low mass stars via annual trigonometric parallax → observations of star clusters (Main Sequence Fitting, Moving Cluster Method) which contain low mass stars yield distances to the clusters (→ can infer the distances and hence luminosities of the bright stars in the cluster and thankfully many clusters contain Cepheid variables). |
Before the Hubble Space Telescope, typical extra-galactic distance ladders looked like
Milky Way -----> 12 M l.y. ------> 80 M l.y. ---------> 300 M l.y. ---------> 5 B l.y.
Cepheids large HII regions, Galaxy methods (types, Type Ia SN,
brightest stars n-th brightest galaxy in
a cluster, ... )
------------------------------------------------->
Tully-Fisher Method
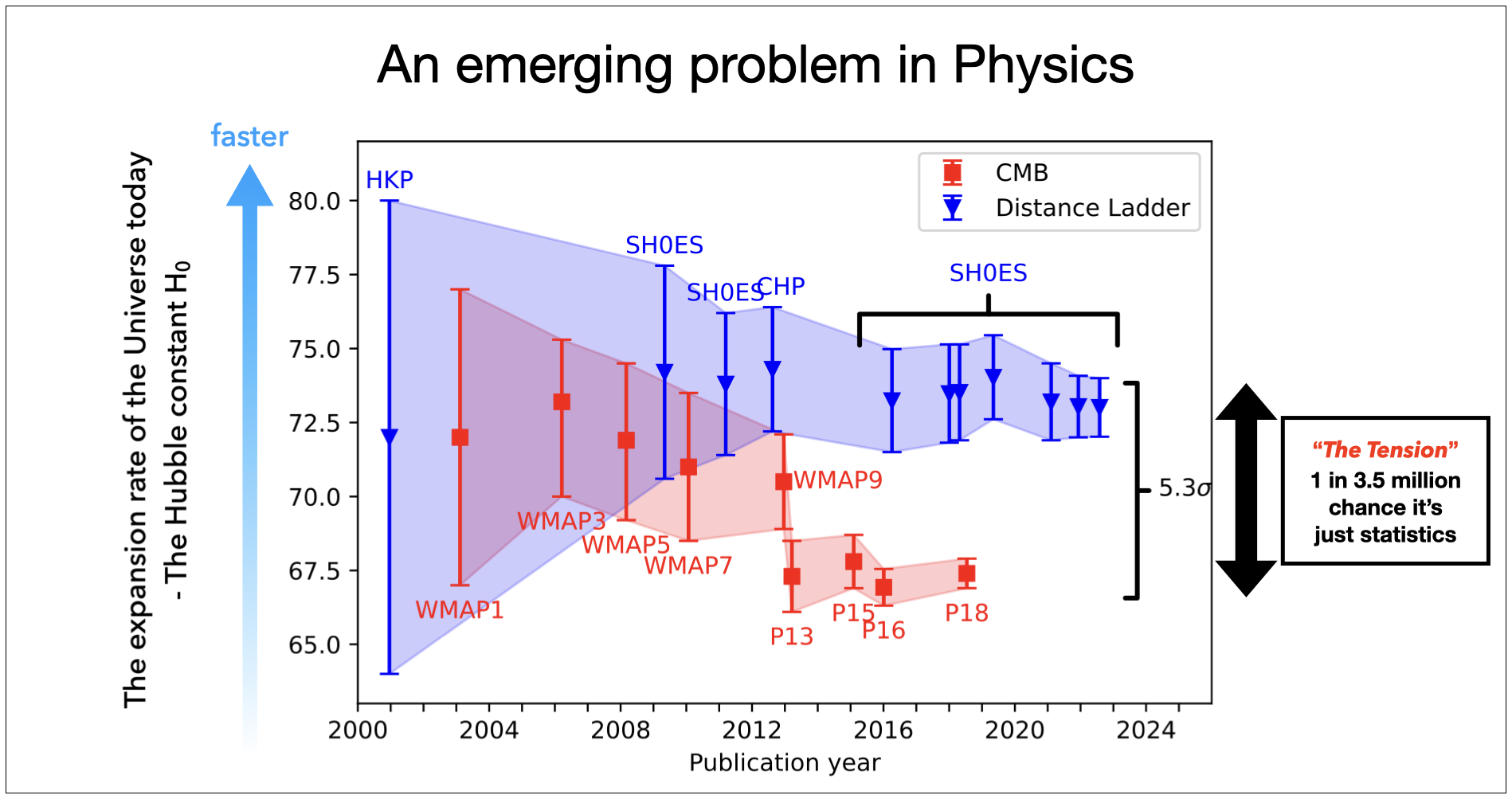
Unfortunately, results from different workers led to different answers for Ho. The problems in distance determinations arose even by the Virgo cluster of galaxies (distance of 65 Million light years); the different methods gave distance estimates that differed by around a factor of 2. The differences in the Hubble constant → different ages for the Universe. Some workers found that the Universe was less than 10 billion years old while other workers found that it was closer to 20 billion years old!
When the Hubble Space Telscope (HST) studied Cepheids in M100 and other galaxies in the Virgo cluster of galaxies, it firmed up the distance to Virgo and was thus able to re-calibrate the distance ladder.
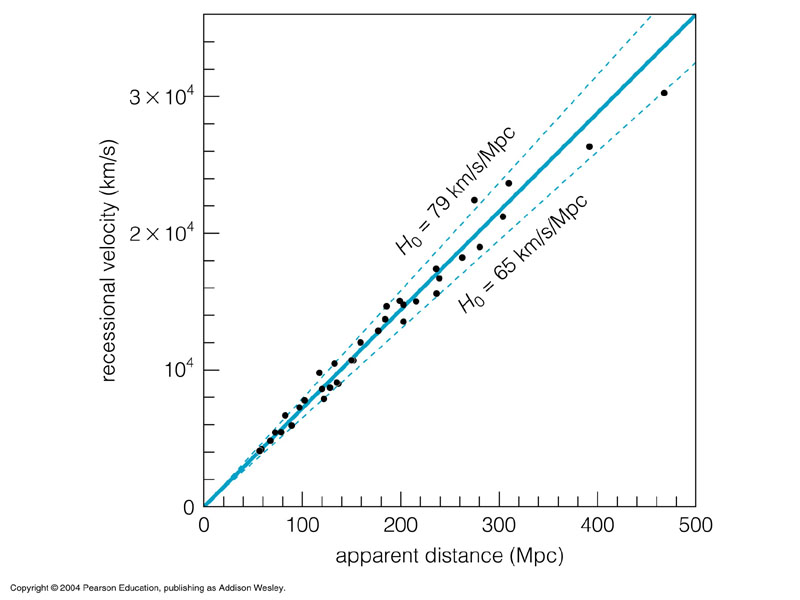
The HST results led to our modern value for the Hubble constant of Ho.
 |
→ the critical density is ~ 10-29 grams per cubic centimeter |
 |
|