Research

Soft matter physics aims to understand complex materials and systems that owe their physical properties to interactions among mesoscopic building blocks, often strongly influenced by disorder and stochastic fluctuations. From its origins in studies of polymers and liquid crystals, the field of soft matter has grown to encompass a wide range of systems and techniques.
Our group works on a variety of problems involving elasticity, mechanics, and statistical physics, with two main sources of inspiration:
-
Designer matter: Thanks to advances in fabrication techniques ranging from rapid prototyping to self-assembly, we have an ever-improving ability to fabricate desired structures across varied length scales. This motivates the question: if we can build any material, what should we build? How do we design structures that harbour novel and potentially useful mechanical properties?
-
Biology: Biological structures such as DNA, cell membranes and the cytoskeleton are textbook examples of “soft matter”, whose shape and mechanical properties emerge from interactions among mesoscopic building blocks and are strongly influenced by stochastic forces due to temperature and active metabolic processes. Geometry and randomness are also key players in the propagation of genetic information through time and space during evolution.
These problems are tackled through a combination of theoretical and computational techniques. We also benefit from collaborations with experimental groups and from conducting our own laboratory demonstrations when the opportunity arises.
Below are summaries of current and past research projects under these themes.
Designer matter
Active metamaterials

Active matter refers to collective states of interacting, dynamic agents which expend energy. Rooted in studies of living systems such as bird flocks and the cytoskeleton, the field is now exploring ways in which artificial materials with dynamical elements may display mechanical properties with novel and potentially desirable features. How do classical notions of materials science, such as elasticity and rigidity, translate to such active materials? What new frameworks and techniques might we need to design, assemble, and characterize them?
Publications:
Topological soft matter

The topological bulk-boundary correspondence is a powerful concept in condensed matter physics, which links the edge excitations of a structure (whether of electrons, light, or sound) to a topological invariant that characterizes its bulk. As a result, these edge modes are robust against a wide range of perturbations as long as they do not change the bulk invariant. We have designed repeating structures, or metamaterials, with robust mechanical properties of topological origin. We are also exploring the realization of topologically protected phenomena in polymer physics.
Publications:
(Chosen for the cover of the February 2015 issue of Nature Physics, and with an accompanying commentary.)
Biophysics and evolutionary dynamics
Long-range dispersal and genetic diversity

The spreading of genetic information over long distances is common in nature, from wind- and water-borne seeds and microbes to the hitchhiking of pathogens on air travellers. By providing access to virgin territory with little competition, even rare long-distance dispersal events can dramatically accelerate the spread of a species or a beneficial mutation within a species. We aim to understand the population structures that can arise when multiple mutations, which may be neutral relative to each other or confer some defined fitness advantage, spread through a population with the help of long-range dispersal events. Do such populations end up being more or less diverse than populations where genetic information spreads locally? What are the signatures of long-range dispersal in genetic data such as site frequency spectra?
Publications:
Elasticity and geometry of thin-walled structures
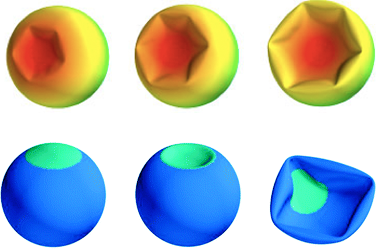
The mechanics of thin shells governs the stiffness and response of many biological structures such as bacterial and plant cell walls and the outer protein shell of viruses. In contrast to macroscopic shell structures, living shells are dynamic objects buffetted by thermal fluctuations and by the molecular machinery involved in growth and replication. Understanding their elastic response entails combining classical shell theory with equilibrium and nonequilibrium statistical mechanics to take into account the effects of stochastic forces. Spatial inhomogeneities in stiffness and the addition of material due to growth are also important considerations. The goal is to develop an expanded shell theory framework that could be applied to biological problems such as shape regulation in cell wall growth and mechanical degradation of viruses.
