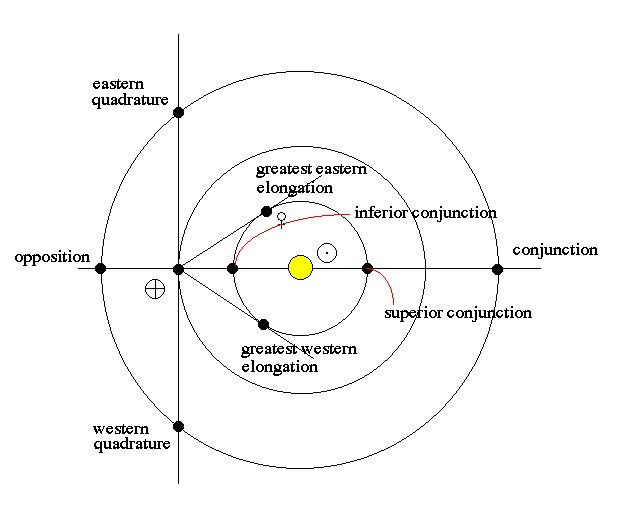
With the success of the heliocentric model, the order of the planets with respect to distance from the Sun is known by the 15th century (but not their actual distances). The planets outside of the Earth's orbit (Mars, Jupiter, Saturn, Uranus, Neptune) are called superior planets. The planets inside of the Earth's orbit (Mercury, Venus) are called inferior planets.

Other configurations are:

• Object at greatest western elongation = "morning star"
• Object at greatest eastern elongation = "evening star"
• only inferior planets have phases
• transit = passage of an inferior planet across the Sun

Galileo's laws of Motion:

To understand the orbits of the planets we need to understand motion in general and, in particular, the cause of motion.

Aside from his numerous inventions, Galileo also laid down the first accurate laws of motion for masses. Galileo realized that all bodies accelerate at the same rate regardless of their size or mass. Everyday experience tells you differently because a feather falls slower than a cannonball. Galileo's genius lay in spotting that the differences that occur in the everyday world are in incidental complication (in this case, air friction) and are irrelevant to the real underlying properties (that is, gravity). He was able to abstract from the complexity of real-life situations the simplicity of an idealized law of gravity.

Key among his investigations are:

• developed the concept of motion in terms of velocity (speed and direction) through the use of inclined planes.
• developed the idea of force, as a cause for motion.
• determined that the natural state of an object is rest or uniform motion, i.e. objects always have a velocity, sometimes that velocity has a magnitude of zero = rest.
• objects resist change in motion, which is called inertia.

Kepler's laws of Planetary Motion:

Kepler developed, using Tycho Brahe's observations, the first kinematic description of orbits, Newton will develop a dynamic description that involves the underlying influence (gravity). Kepler formulated three laws of planetary motion (that also applies to asteroids, comets and spacecraft).

• 1st law (law of elliptic orbits): Each planet moves in an elliptical orbit with the Sun at one focus.

Ellipses that are highly flattened have high eccentricity. Ellipses that are close to a circle have low eccentricity.
• 2nd law (law of equal areas): a line connection the Sun and a planet (called the radius vector) sweeps out equal areas in equal times
  

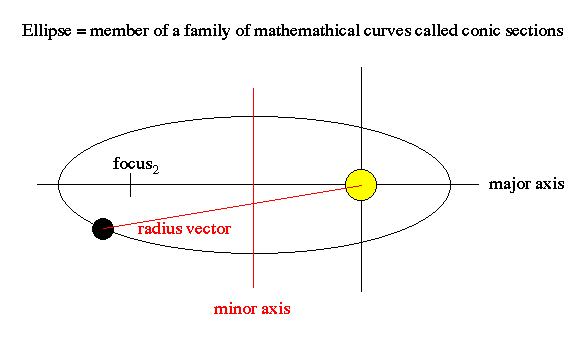
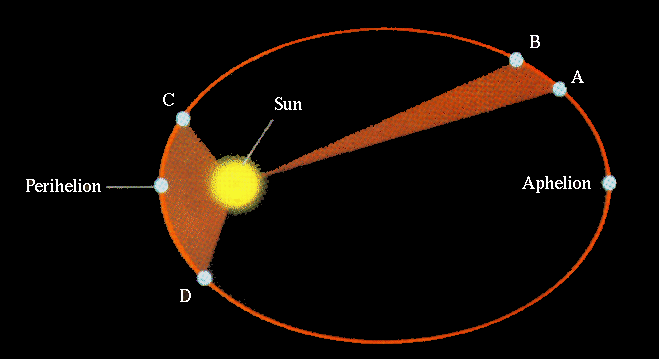
  Objects travel fastest at the low point of their orbit, and travel slowest at the high point of their orbit.

• 3rd law (law of harmonics): The square of a planet's orbital period (the time it takes to go around the Sun) is proportional to its mean distance from the Sun cubed.

  The mathematical way to describe Kepler's 3rd law is:

  P² α R³

  where the α symbol means `proportional to'. Proportions are expressions that imply there exists some constant, k, that relates the period, P, and the radius, R, such that

  P² = kR³

  We can determine k by expressing the formula in units of the Earth and its orbit around the Sun, such that

  (1 yr)² = k (1 A.U.)³

  so k is equal to one, as long as we use units of years and A.U.'s (the Astronomical Unit, i.e. the distance from the Earth from the Sun). With k=1, then Kepler's 3rd law becomes

  P² = R³

  The 3rd law is used to develop a ``yardstick'' for the Solar System, expressing the distance to all the planets relative to Earth's orbit by just knowing their period (timing how long it takes for them to go around the Sun).

Orbits:

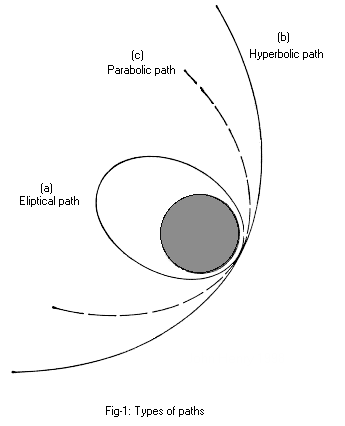
Many years after Kepler, it was shown that orbits actually come in many flavors, ellipses, circles, parabolas and hyperbolas; a family of curves called conic sections. There are five basic types of simple orbits: radial, ballistic, stable, polar and geosynchronous.

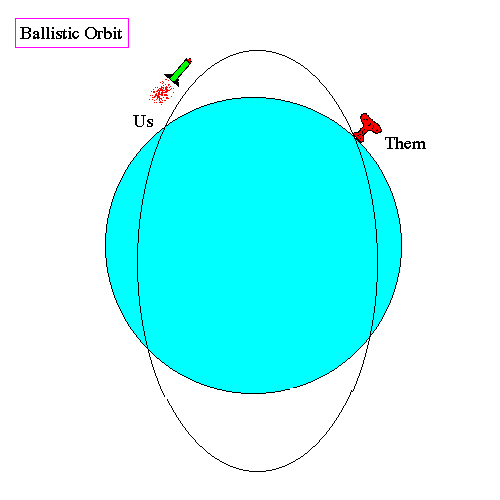
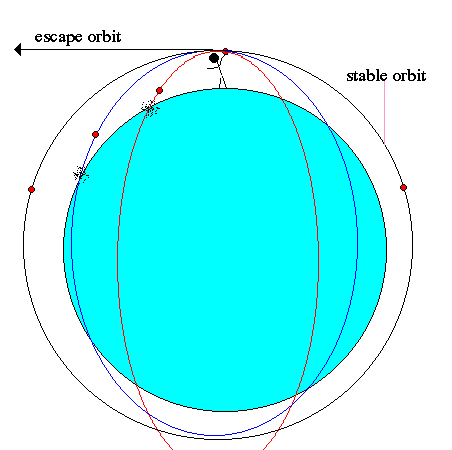
The direction a body travels in orbit can be direct, or prograde, in which the spacecraft moves in the same direction as the planet rotates, or retrograde, going in a direction opposite the planet's rotation.

The semi-major axis of an orbit is determined by the kinetic energy acquired by the rocket at burnout. This is equivalent to the burnout velocity. For low burnout velocities (below 25,000 ft/sec) the orbit is ballistic, meaning it does not escape the surface of the Earth. Burnout velocities above 25,000 ft/sec achieve stable orbit. At 35,000 ft/sec, the orbit reaches the distance of the Moon.

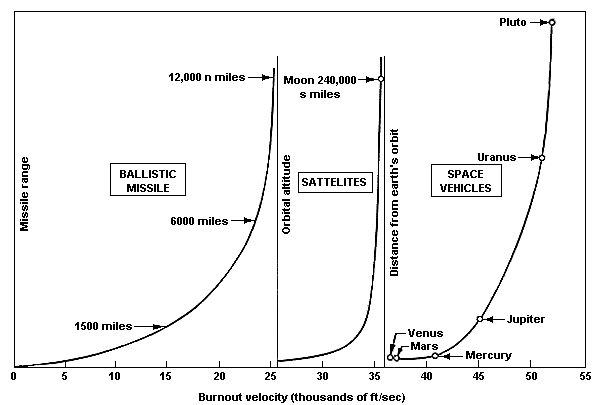
The amount of burnout velocity also determines the orbit type, an ellipse, a parabola or a hyperbolic path.

Satellites use a wide variety of orbits to fulfil their missions. The orbit chosen for a satellite is a compromise between the mission requirements, the capabilities of the rocket used to launch the satellite and orbital mechanics.

• The orbital period. This increases with the mean altitude of the orbit, so a satellite in a low earth orbit moves faster than a satellite in a geostationary orbit. Also the velocity of a satellite in an eccentric orbit varies along the orbit, being fastest at perigee & slowest at apogee (Keplers second law of equal areas).
• Inclination. The angle between the plane (major axis) of the satellite orbit and the equator
• Eccentricity: A perfectly circular orbit has an eccentricity of zero, an elliptical orbit an eccentricity of 0< to <1, a parabolic orbit an eccentricity of 1 and a hyperbolic orbit of >1. The low point of an orbit is known as perigee, whilst the high point is apogee. The major axis is the vector connecting the perigee to the apogee.
• The ascending node is where the orbit crosses the equator in a northbound direction (i.e., the direction of the satellite motion). Likewise, the descending node is where the orbit crosses the equator in a southbound direction.

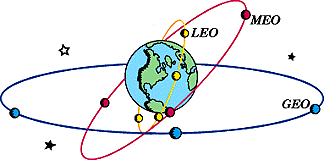
Low Earth Orbit:

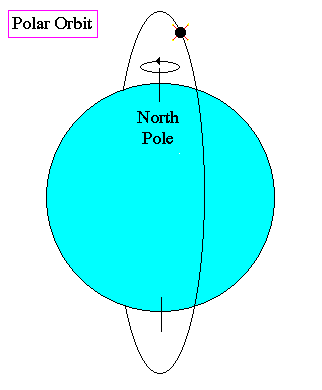
Weather and spy satellites use over pole orbits so that Earth turns under them once per day, i.e. total coverage of the Earth's surface

• Circle of visibility = yellow circle around satellite indicating the region of the earth visible from the satellite.
• Part of orbit in sunlight = yellow.
• Part of orbit in shadow = red.
• Dayside of earth = light blue.
• Nightside of earth = dark blue.

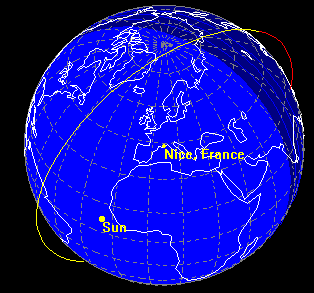
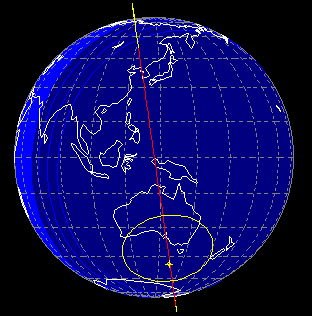
In theory an orbit should remain fixed in space whilst the earth rotates beneath the satellite. In reality the earth is slightly bulged and the effect of this bulge is to shift the point of perigee and the ascending node for any orbit which has an inclination other than 90. This effect is known as nodal regression, the result of which is that the plane of the orbit rotates or precesses.

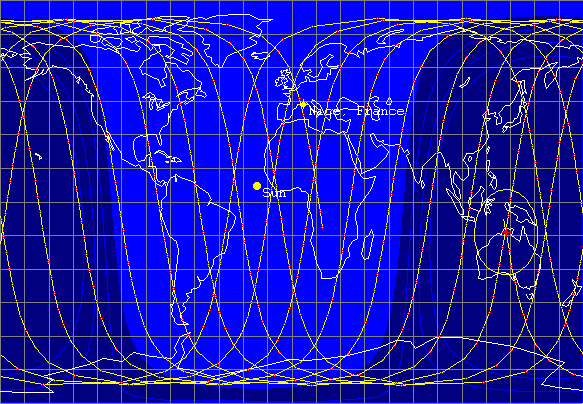
However, this effect is used to advantage here to shift the orbit at exactly the same rate as the daily change in position of the sun over any point of the earth. So the satellite always passes over the earth on the sunlit part of its orbit at the same local time of day (for example at 9 am local time). This ensures that lighting conditions are similar (ignoring seasonal differences) for images taken of the same spot on the earth at different times. Additionally the orbit is resonant with the rotation period of the earth, meaning that the satellite passes over the same point on the earth at the same time of day at regular intervals (which may be daily or every 2 or more days depending on the resonance). In the case of Landsat there are 14.5 orbits per day or 29 orbits every 2 days.

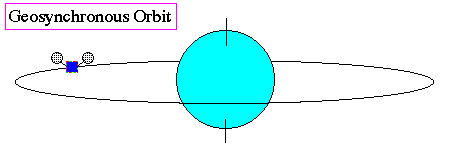
Geosynchronous Orbits (GEO):

Communication satellites use geosynchronous orbits for continuous coverage of one region of the globe, i.e. the orbital period is exactly one day. This turns out to be approximately 24,000 miles up.

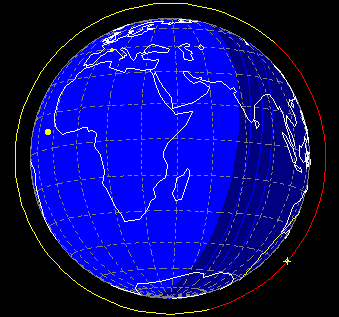
Below is shown the orbit of the TDRS-7 satellite, one of a series of NASA satellites which used to provide a near continous communications link with the Space Shuttle, International Space Station & other spacecraft such as the Hubble Space Telescope.

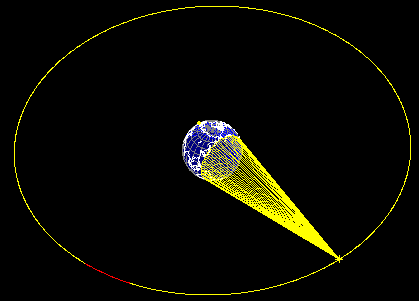
Compared with the LEO orbit of the ISS, a much larger portion of the earth's surface is visible from the TDRS-7 spacecraft. The zone of visibility of the spacecraft has been highlighted by a cone. Approximately 40% of the earths surface can be viewed at any one time from geostationary altitude. Additionally, the spacecraft orbit is sunlight apart from a small zone which passes into the earths shadow. Actually, geostationary satellites only experience eclipses at two periods of the year - for a few weeks at a time at the spring and autumn equinoxes. The reason for this is simple. The earths rotation axis is inclined with respect to the ecliptic, hence the earth's shadow cone misses the plane of a zero inclination geostationary orbit apart from the times when the suns declination is close to zero. This occurs twice a year, once at the spring equinox and once at the autumn equinox.

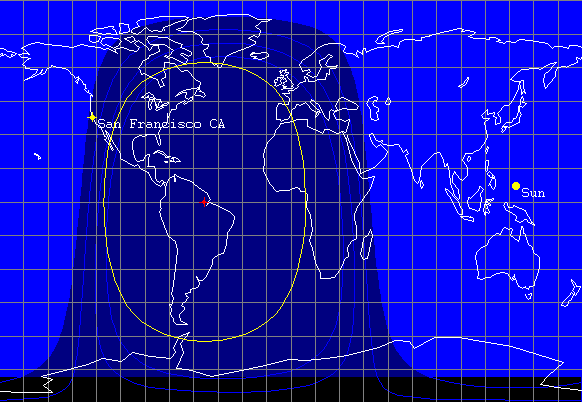
As can be seen from this graphic a perfectly geostationary satellite stays over the same spot on the equator all day. However, if we were to look closely we would see that the satellite does appear to change position, generally describing a small figure of 8 or an arc due to the effect of lunar / solar perturbations dragging the satellite into a slightly elliptical, slightly inclined orbit. There are many non operational satellites in "graveyard" orbits slightly above or below a true geostationary orbit. Since the orbital period is slightly more or less than the earths rotation period these satellites appear to drift slowly around the earth.