Reductionism:

 Readings: Clockwork Universe
Strict Determinism
World Views

Reductionism is the belief that any complex set of phenomena can be defined or explained in terms of a relatively few simple or primitive ones.

For example, atomism is a form of reductionism in that it holds that everything in the Universe can be broken down into a few simple entities (elementary particles) and laws and interactions among them. Modern chemistry reduces chemical properties to ninety or so basic elements (kinds of atoms) and their rules of combination.

To a reductionist, once a set of equations or mathematical relations has been found to describe a system, then the behavior of the system is considered to be explained.

Reductionism is very similar to, and has its roots from, Occam's Razor, which states that between competing ideas, the simplest theory that fits the facts of a problem is the one that should be selected.

Reductionism was widely accepted due to its power in prediction and formulation. It is, at least, a good approximation of the macroscopic world (although it is completely wrong for the microscope world, see quantum physics).

Too much success is a dangerous thing since the reductionist philosophy led to a wider paradigm, the methodology of scientism, the view that everything can and should be reduced to the properties of matter (materialism) such that emotion, aesthetics and religious experience can be reduced to biological instinct, chemical imbalances in the brain, etc. The 20th century reaction against reductionism is relativism. Modern science is somewhere in between.

Determinism:

Closely associated with reductionism is determinism, the philosophy that everything has a cause, and that a particular cause leads to a unique effect. Another way of stating this is that for everything that happens there are conditions such that, given them, nothing else could happen.

Implicit to determinism is the fact that every event happens of necessity. It has to happen; the Universe has no choice.

Clockwork Universe:

The 17th century was a time of intense religious feeling, and nowhere was that feeling more intense than in Great Britain. There a devout young man, Isaac Newton, was finally to discover the way to a new synthesis in which truth was revealed and God was preserved.

Newton was both an experimental and a mathematical genius, a combination that enabled him to establish both the Copernican system and a new mechanics. His method was simplicity itself: "from the phenomena of motions to investigate the forces of nature, and then from these forces to demonstrate the other phenomena." Newton's genius guided him in the selection of phenomena to be investigated, and his creation of a fundamental mathematical tool--the calculus (simultaneously invented by Gottfried Leibniz)--permitted him to submit the forces he inferred to calculation. The result was Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy, usually called simply the Principia), which appeared in 1687. Here was a new physics that applied equally well to terrestrial and celestial bodies. Copernicus, Kepler, and Galileo were all justified by Newton's analysis of forces. Descartes was utterly routed.

Newton's three laws of motion and his principle of universal gravitation sufficed to regulate the new cosmos, but only, Newton believed, with the help of God. Gravity, he more than once hinted, was direct divine action, as were all forces for order and vitality. Absolute space, for Newton, was essential, because space was the "sensorium of God," and the divine abode must necessarily be the ultimate coordinate system.

Newtonian mechanics came to be regarded as the ultimate explanatory science: phenomena of any kind, it was believed, could and should be explained in terms of mechanical conceptions. Newtonian physics was used to support the deistic view that God had created the world as a perfect machine that then required no further interference from Him, the Newtonian world machine or Clockwork Universe. These ideals were typified in Laplace's view that a Supreme Intelligence, armed with a knowledge of Newtonian laws of nature and a knowledge of the positions and velocities of all particles in the Universe at any moment, could deduce the state of the Universe at any time.

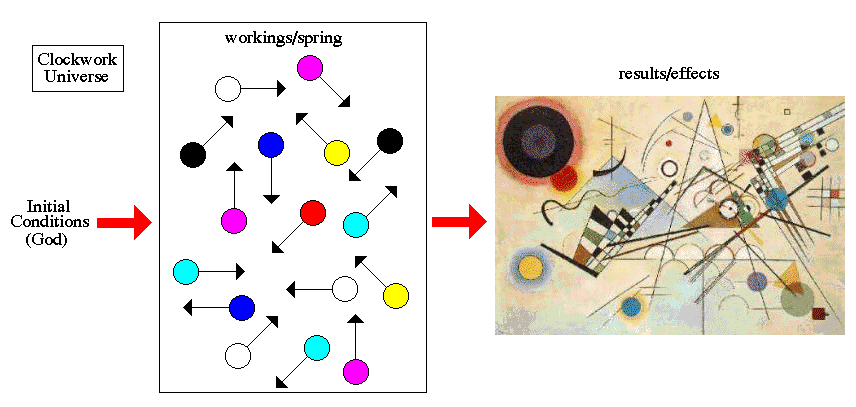
Determinism also implies that everything is predictable given enough information. Since Newtonian or classical physics is rigidly determinist, both in the predictions of its equations and its foundations, then there is no room for chance, surprise and creativity. Everything is as it has to be.

Needless to say, obtaining a completely detailed description of the entire Universe at any one time was not a realistic undertaking, nor was solving all the equations required to predict its future course. But that wasn't the point. It was enough that the future was ordained. If you accepted the proposition that humans were entirely physical systems, composed of particles of matter obeying physical laws of motion, then in principle, every future human action would be already determined by the past. For some this was the ultimate indication of God: where there was a design there must be a Designer, where there was a clock there must have been a Clockmaker. For others it was just the opposite, a denial of the doctrine of free will which asserts that human beings are free to determine their own actions. Even for those without religious convictions, the notion that our every thought and action was pre-determined in principle, even if unpredictable in practice, made the Newtonian Universe seem strangely discordant with our everyday experience of the vagaries of human life.

Celestial Mechanics:

Newton went beyond his simple laws of motion and gravitation to develop a whole set of mathematics to describe and calculate orbits. Today we can this mathematics calculus. And the science of applied calculus to orbits is called celestial mechanics. The key to calculus is the use of vectors. A vector is a quantity that has both magnitude and direction. It is typically represented symbolically by an arrow in the proper direction, whose length is proportional to the magnitude of the vector. Although a vector has magnitude and direction, it does not have position. A vector is not altered if it is displaced parallel to itself as long as its length is not changed.

Newton applied vectors in terms of force. A body is added on by a vector force as shown above. Forces can be added just like vectors, so that force 1 and force 2 add together to produce the total force, F. Total force F can also be broken into components x and y that correspond to the forces in the x and y directions (for example, along a road and with gravity).

A particle moving with constant velocity v suffers a displacement s in time t given by s = vt. The vector v has been multiplied by the scalar t to give a new vector, s, which has the same direction as v but cannot be compared to v in magnitude (a displacement of one meter is neither bigger nor smaller than a velocity of one meter per second). This is a typical example of a phenomenon that might be represented by different equations in differently oriented Cartesian coordinate systems but that has a single vector equation (for all observers not moving with respect to one another).

For a particle of mass m, a force is applied with results in an acceleration a. The acceleration changes the velocity vector by a small amount, delta v, every interval of time, delta t. This results in trajectories, a vector map of the changes in position from an origin, the vector x and the velocities, vector v.

With vector calculus, Newton was able to develop a cosmology which included the underlying cause of planetary motion, gravity, completed the solar system model begun by the Babylonians and early Greeks. The mathematical formulation of Newton's dynamic model of the solar system became the science of celestial mechanics, the greatest of the deterministic sciences.

Although Newtonian mechanics was the grand achievement of the 1700's, it was by no means the final answer. For example, the equations of orbits could be solved for two bodies, but could not be solved for three or more bodies. The three body problem puzzled astronomers for years until it was learned that some mathematical problems suffer from deterministic chaos, where dynamical systems have apparently random or unpredictable behavior.

Artificial Life:

One of the most profound objections to the reductionist way of thinking is that the Universe is filled with complexity (Hamlet, people, the Earth, galaxies). But how? It is not at all obvious that a complex world can be constructed from simple premises.

Our understanding of the limits of the clockwork Universe and determinism was greatly expanded by the introduction of computers in the 1960's. Clearly, computers are powerful tools for the analysis of scientific data, but what is little known to the general public is that computers were also extremely important in exploring a new mathematical world of computable operations. This leads to the discovery of what is known as the recursive Universe, a Universe where, even with strict determinism, still has creativity and originality due to the rules of complexity (sometimes called chaos theory).

One of the first areas explored with high speed computers was the field of cellular automata or artificial life. There is no systematic way to decide in advance whether a given mathematical problem is decidable or undecidable by the operation of a machine, i.e. the fate of the machine cannot be known in advance. Therefore, the fate of cellular automata patterns cannot be systematically known in advance, even though the evolution of such patterns are strictly deterministic. Randomness and uncertainty are built into the Universe due to the restrictions of logic itself, as soon as systems become complex enough to engage in self-reference.

The concept of computable truths can be explored through simple games such as Conway's game of Life:

Conway's Life

The Game of Life is actually a non-game, as the computer makes all the moves and the only free parameters are the initial set-up. Yet the Life game board becomes filled with a rich tapestry of creatures and shapes. For example, many of the simplest patterns either die off quickly or become "still-life", unchanging shapes (such as the block, loaf and beehive). Others oscillate with cycle times from 2 to dozens of timesteps (e.g., blinker, clock and pulsar). Life became very interesting with the discovery of a five cell pattern that "walked" across the Life playing field (called glider for its amoeba like behavior) hinting at the ability to transfer information across the Life space.

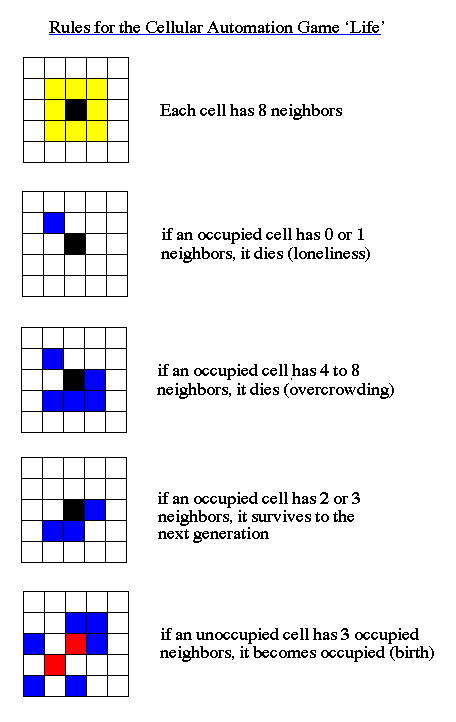
One the earliest questions with regard to computer driven creatures using deterministic rules is if one could find a pattern that grows forever. This is a difficult question since the only "proof" would be to run the simulation forever, which is not practical. Numerous avenues of new math were invented in an attempt to handle the issues in an artificial world, but the question was quickly answered with the discovery of a glider gun, a pattern that produces glider at regular intervals which then fly off into space forever.

As the power of computers increased, the sophistication of Life gamers also increased with the development of new tools to explore the rich Life "ecosphere". Most patterns become random field (called broth) which start out with violent activity then resolving themselves into familiar Life objects (blocks, blinkers, gliders, etc). The more often an object is seen in a random field the more "natural" it is considered.

Soon an almost endless series of patterns with unusual behaviors were discovered. Gliders and spaceships, spaceship factories, puffer trains, breeders, eaters, gardens of eden, methuselahs, reflectors, and so on. There is every indication that, with sufficient processing power, the Life universe can be just as rich and diverse as our own universe with the possibility of self-reproducing patterns and evolution. All from strict determination rules.

bigun bhepto baker max mirage breeder hotel

The behavior of complex systems is not truly random, it is just that the final state is so sensitive to the initial conditions that it is impossible to predict the future behavior without infinite knowledge of all the motions and energy (i.e. a butterfly in South America influences storms in the North Atlantic).

Although this is `just' a mathematical game, there are many examples of the same shape and complex behavior occurring in Nature.

The key point to complex behavior is that simple rules can lead to very exotic and complicated patterns. And, most importantly, these patterns are unpredictable.

Deterministic Chaos:

It has always been assumed that determinism goes hand and hand with predictability. For example, consider the following geometric construction. Each point on the top line is uniquely associated with a point on the bottom line. Any point close to a point (P' with respect to P) will have corresponding point (Q' with respect to Q). Small errors in our knowledge of the position of P will only produce small errors in our knowledge of the position of Q. If this is a physical system, then we would call this predictability.

In contrast to the above situation, P and P' on the arc of a circle are associated with the more widely separated points Q and Q' (where Q is found by drawing a line from the top of the circle through P). The sensitivity becomes more pronounced as P gets closer to the top of the circle. Slight errors in P produce big errors in the location of Q despite the fact that points on the horizontal line are uniquely determined by those on the circle.

Are things chaotic because we lack sufficient information? Consider a line. To label every point on the line, you need not all possible rational numbers, but all irrational numbers as well. So the typical real number can only be expressed as a decimal expansion consisting of an infinite string of digits with no systematic pattern to it, a random sequence. One could use all the atoms in the entire Universe and still not be able to encode the information to record one irrational number with complete precision.

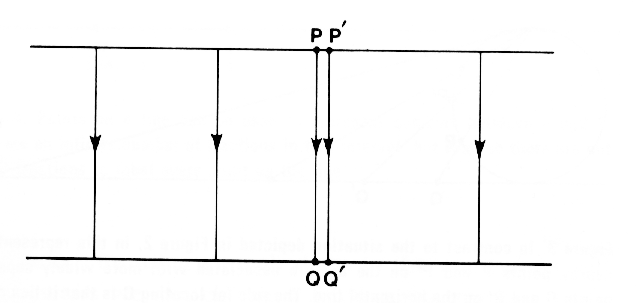
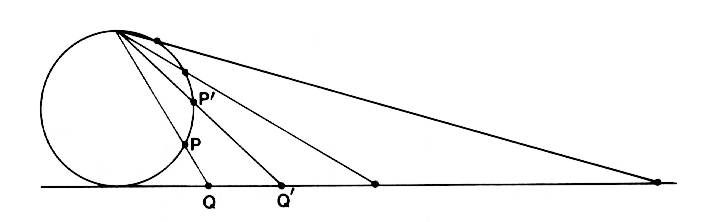
Determinism implies predictability only in the idealized limit of infinite precision. The Universe itself cannot know its own workings with absolute precision, and there cannot predict what will happen next in every detail. Deterministic chaos seems random because we are necessarily ignorant of the ultrafine details and so is the Universe itself.

The best way to study chaotic behavior, also called nonlinear behavior, is with the use of a this pendulum.

Notice that complicated behavior does not necessarily imply complicated forces or laws. Even with deterministic laws, the future states of the Universe are open and this bestows upon Nature an element of creativity, an ability to bring forth that which is genuinely new.

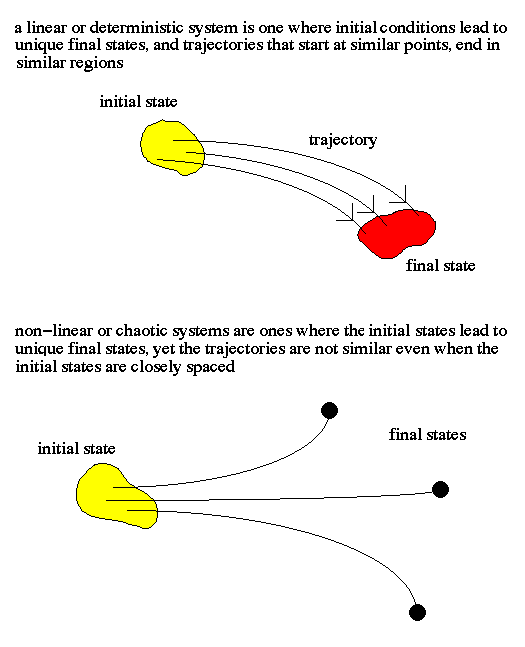
Chaotic systems are examples of unstable motion because each trajectory is identified with distinct initial conditions that, no matter how close, diverge exponentially over time. In deterministic chaos the equations of motion are deterministic, but the outcome appears random due to the sensitivity to initial conditions.

The errors in chaotic systems grow at an exponential rate. So that the randomness of chaotic motion is not simply the result of our ignorance of the initial conditions, but rather is fundamental. More information must be processed to maintain the same level of accuracy and, thus, the system is truly unpredictable.

Indeed, when we consider chaos and incompleteness we find that the world is rich in truth and creativity because of their existence, not in spite of. Whatever real-world truths might exist, the overwhelming majority of them cannot be the counterparts of theorems in an formal logical system. The gap between proof and truth can be narrowed, but never closed.

Irreversibility:

Classical physics is a science upon which our belief in a deterministic, time-reversible description of Nature is based. Classical physics does not include any distinction between the past and the future. The Universe is ruled by deterministic laws, yet the macroscopic world is not reversible. This is known as Epicurus' clinamen, the dilemma of being and becoming, the idea that some element of chance is needed to account for the deviation of material motion from rigid predetermined evolution.

The astonishing success of simple physical principles and mathematical rules in explaining large parts of Nature is not something obvious from our everyday experience. On casual inspection, Nature seems extremely complex and random. There are few natural phenomenon which display the precise sort of regularity that might hint of an underlying order. Where trends and rhythms are apparent, they are usually of an approximate and qualitative form. How are we to reconcile these seemingly random acts with the supposed underlying lawfulness of the Universe?

For example, consider falling objects. Galileo realized that all bodies accelerate at the same rate regardless of their size or mass. Everyday experience tells you differently because a feather falls slower than a cannonball. Galileo's genius lay in spotting that the differences that occur in the everyday world are in incidental complication (in this case, air friction) and are irrelevant to the real underlying properties (that is, gravity). He was able to abstract from the complexity of real-life situations the simplicity of an idealized law of gravity. Reversible processes appear to be idealizations of real processes in Nature.

Probability-based interpretations make the macroscopic character of our observations responsible for the irreversiblity that we observe. If we could follow an individual molecule we would see a time reversible system in which the each molecule follows the laws of Newtonian physics. Because we can only describe the number of molecules in each compartment, we conclude that the system evolves towards equilibrium. Is irreversiblity merely a consequence of the approximate macroscopic character of our observations? Is it due to our own ignorance of all the positions and velocities?

Irreversibility leads to both order and disorder. Nonequilibrium leads to concepts such as self-organization and dissipative structures (Spatiotemporal structures that appear in far-from-equilibrium conditions, such as oscillating chemical reactions or regular spatial structures, like snowflakes). Objects far from equilibrium are highly organized thanks to temporal, irreversible, nonequilibrium processes.

Individual descriptions are called trajectories, statistical descriptions of groups are called ensembles. Individual particles are highly deterministic, trajectories are fixed. Yet ensembles of particles follow probable patterns and are uncertain. Does this come from ignorance of all the trajectories or something deeper in the laws of Nature? Any predictive computation will necessarily contain some input errors because we cannot measure physical quantities to unlimited precision.

Note that relative probabilities evolve in a deterministic manner. A statistical theory can remain deterministic. However, macroscopic irreversiblity is the manifestation of the randomness of probabilistic processes on a microscopic scale. Success of reductionism was based on the fact that most simple physical systems are linear, the whole is the sum of the parts. Complexity arrives in nonlinear systems.