bfh_python

A bordered Heegaard Floer computation package

The mathematics underlying bfh_python

This is a brief introduction to bordered Floer homology and Zhan's extension of it, to help with using the bfh_python package. For more details, see the references below.

The basics

bfh_python computes HF-hat by a divide and conquer algorithm. Roughly, to a closed surface F it associates a differential algebra A(F). To a 3-manifold Y with boundary F, it associates a right A(F)-module CFA(Y) and a left A(-F)-module CFD(Y). More generally, to a 3-dimensional cobordism Y from F1 to F2 it associates a bimodule CFDA(Y).

Then, if a 3-manifold Y is decomposed as follows:

Decomposition of a 3-manifold along surfaces

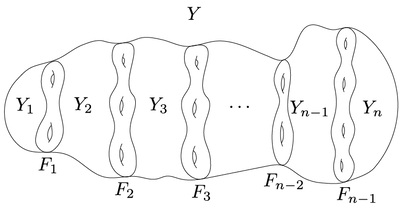
then CF^(Y) is given by

CF^(Y)≃CFA(Y1)⊗A(F1)CFDA(Y2)⊗A(F2)CFDA(Y3)⊗A(F3) …⊗A(Fn-2)CFDA(Yn-1)⊗A(Fn-1)CFD(Yn).

This is called the pairing theorem in bordered Floer homology.

More precisely, A(F) is associated to a minimal handle decomposition of F, called a pointed matched circle. For surfaces of genus bigger than one, there are many non-equivalent pointed matched circles; here are three for the genus 2 case:

Genus 2 pointed matched circles

These are easy to generate, and these particular three (the split, antipodal, and linear pointed matched circles) there are helper functions:

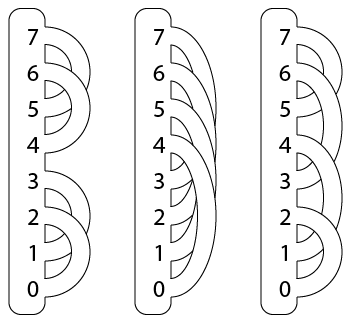
PMC([(0,2),(1,3),(4,6),(5,7)]
PMC([(0,4),(1,5),(2,6),(3,7)]
PMC([(0,2),(1,4),(3,6),(5,7)]
splitPMC(2)
linearPMC(2)
antipodalPMC(2)

The package does not directly know the bimodule associated to an arbitrary cobordism, but it does know:

  • The modules CFD(H) associated to certain handlebodies H—the "zero-framed" and "infinity-framed" handlebodies with boundary the split pointed matched circle, and the "plat handlebody" with boundary the linear pointed matched circle. Those have the following bordered Heegaard diagrams. (If you know what a Heegaard diagram for a 3-manifold with boundary but not a bordered Heegaard diagram, you get an ordinary Heegaard diagram by forgetting all the arcs):

    Three genus 2 handlebodies

    (The corresponding functions are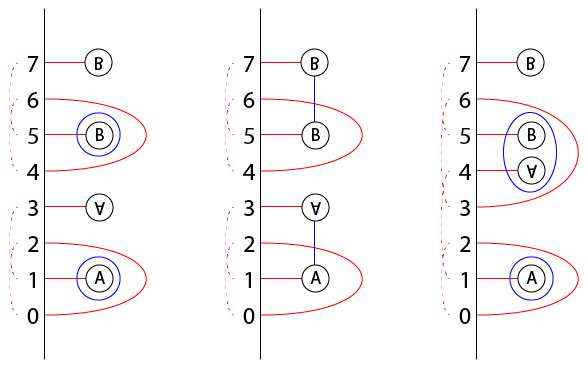 zeroTypeD(genus), infTypeD(genus), and platTypeD(genus). There's also a zeroTypeDAdm(genus) which gives the invariant of an admissible version of the 0-framed diagram.)

  • The bimodules CFDA(φ) associated to (the mapping cylinder of) certain generators of the mapping class groupoid, called arcslides. These are the obvious diffeomorphisms associated to changing a pointed matched circle by sliding one foot of a 1-handle over an adjacent 1-handle; here is a pair of arcslides which compose to a Dehn twist around the specified circle γ.

    Two arcslides composing to a Dehn twist

    More about this generating set can be found in the papers by Andersen-Bene-Penner and Bene below, as well as in "Computing HF-hat by factoring mapping classes". The class for arcslides themselves is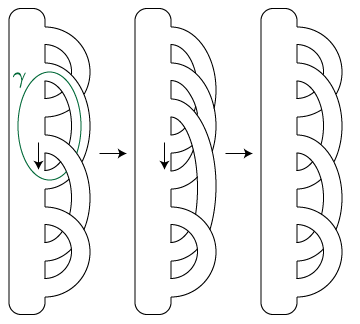 Arcslide(), while the class for their bimodules is ArcslideDA(). (The first of the two arcslides is Arcslide(linearPMC(2),4,3).)

  • The bimodules associated to 3-dimensional 1-handle and 2-handle cobordisms, which change the genus of the boundary by ±1. In terms of pointed matched circles, these insert or delete a copy of the genus-1 pointed matched circle somewhere inside the given one. There are two classes, CobordismDALeft() and CobordismDARight(), depending on whether the larger-genus boundary component is on the left or right. (There is also a class Cobordism() which gives CFDD of the cobordism, and assumes the starting and ending cobordisms are linear pointed matched circles.)

This is (more than) enough to compute HF^(Y) for any 3-manifold Y. To do so, you choose a genus g Heegaard splitting of Y. The bimodule CFA of the left handlebody is a composition of g copies of CobordismDARight(). Factor the monodromy as a composition of arcslides, and tensor these bimodules with CFA one at a time. Arrange that the handlebody you want to close off with is 0-framed, say, and tensor on CFD of that handlebody.

At the moment, the code computes tensor products of a module with a bimodule, or of a type A module with a type D module. Tensoring together two bimodules is not implemented.

The computational complexity grows rapidly with the genus, and the code is probably not usually useful above genus 4.

A few other classes have been implemented for convenience when working with branched double covers:

  • AntiBraidDA is the branched double cover of the anti-braid-like resolution of a braid generator, i.e., of a cap followed by a cup. This is equivalent to a CobordismDALeft() follows by a CobordismDARight().
  • DehnSurgeryDA computes the branched double cover of a braid generator, as the mapping cone of a map between the identity braid and AntiBraidDA. This is the bimodule for a Dehn twist on one of the obvious circles in the linear pointed matched circle.

Type D modules and type DA, and DD bimodules

Type D structures, also called twisted complexes or cell modules are a version of projective modules over a differential graded (or A-infinity) algebra. A type D structure over an algebra A consists of a vector space X and a linear map δ1: X→A⊗X. This induces a map A⊗X→A⊗X, which one can think of as the differential module associated to the type D structure; this map is required to be a differential. There is a well-behaved tensor product of an A-infinity module and a type D structure; see the book Bordered Heegaard Floer homology referenced below. Type D structures are convenient to encode, and require storing less information than writing a differential module naively.

There are two useful bimodule analogues of type D structures. The first, type DD structures, or cell bimodules, correspond to bi-projective bimodules: if one views them as bimodules, they are of the form ⊕Aċi⊗jċB where i and j are idempotents in A and B. These are formalized as a vector space X with a map δ1: X→A⊗X⊗B. Tensoring a type DD structure with an A-infinity module gives a type D structure.

The second bimodule analogue used in bfh_python are DA structures. These generalize A-infinity modules and type D structures, but also A-infinity algebra homomorphisms. A type DA structure is formalized as a vector space X with operations δ11+n: X⊗B⊗n→A⊗X. Tensoring a type DA bimodule with a type D structure gives a type D structure, and tensoring a type DA bimodule with an A-infinity module gives an A-infinity module.

A 3-dimensional cobordism Y has bordered invariants CFDD(Y), CFDA(Y), and CFAA(Y), which are type DD, DA, and A-infinity bimodules, respectively. By the pairing theorem, one can convert between them by tensoring with the type DD or AA bimodules associated to the identity cobordism. It turns out that the bimodule CFDD(Id) is easy to describe. One can obtain inefficient models for CFAA from this, or from other techniques (see Bimodules in bordered Floer homology and Heegaard Floer homology as morphism spaces). An efficient way to obtain CFAA(Id) was given and exploited by Zhan in his thesis.

Local DA bimodules

An arcslide diffeomorphism is the identity map outside a small region of the surface. Similarly, a 1- or 2-handle attachment only changes a small part of the surface. This is reflected in the fact that most of the bordered Heegaard diagram representing these 3-manifolds is the same as the bordered Heegaard diagram for F×[0,1] and, consequently, much of the bimodule associated to these diffeomorphisms agrees with the identity bimodule A(F).

In his thesis, Zhan formalizes this by defining a local DA bimodule associated to an arcslide or elementary cobordism. Obtaining the whole DA bimodule from the local DA bimodule is a process he calls extending by the identity. Since the bordered algebras grow rapidly with the genus, so does a naive description of almost any module or bimodule over it. Using local bimodules allows bfh_python to encode the bordered bimodules for arcslides and elementary cobordisms in relatively little space, and tensor with them in relatively little time.

Other versions of the pairing theorem

There is another version of the pairing theorem in terms of Hom instead of tensor product, which is also available in the code. Specifically:

  • If a closed manifold Y is decomposed as Y = Y1∪FY2 then CF^(Y)≃HomA(-F)(CFD(-Y1),CFD(Y2)).
  • If a bordered manifold Y is decomposed as Y = Y1∪FY2, where Y1 has two boundary components, then CF^(Y)≃HomA(-F)(CFDD(-Y1),CFD(Y2)).

These Hom spaces are encoded in the morToD function in the SimpleDStructure and SimpleDDStructure.

Branched double covers

Given a link L in S3, Ozsváth-Szabó constructed a spectral sequence from the Khovanov homology of L to HF^ of the branched double cover Σ(L) of L. This spectral sequence can be computed as follows. Decompose L as a crossingless matching C1 followed by a sequence of braid generators σi1±1σi2±1...σin±1 followed by a crossingless matching C2. Abusing notation, let σij also denote the mapping cylinder of the Dehn twist. Then

CF^(Σ(L))≃CFA(Σ(C1))⊗CFDA(Σ(σi1±1))⊗…⊗CFDA(Σ(σin±1))⊗CFD(Σ(C2)).

There are quasi-isomorphisms

CFDA(Σ(σi)) ≃ Cone(CFDA(Id) → CFDA( Σ(σiv)))
CFDA(Σ(σi)) ≃ Cone(CFDA(Σ(σiv))→ CFDA(Id))

where σiv is the anti-braid-like resolution of σi (i.e., a cap followed by a cup). Tensoring these together for the different braid generators in the decomposition of L gives a cube of resolutions. The associated spectral sequence is the Ozsváth-Szabó spectral sequence.

The bimodule CFDA(Id) is just the algebra itself. The bimodule CFDA(Σ(σiv)) and maps in the formulas above were computed explicitly, and are coded in bfh_python. (In the formulas above, there is some choice of pointed matched circles, but for these computations we used the linear pointed matched circle.) bfh_python can also compute spectral sequences induced by finite, filtered complexes (using what it reasonably calls cancelation constraints), so can compute the Ozsváth-Szabó spectral sequence. (One can also compute this using the Hom-functor version of the pairing theorem in place of tensor products, and type DD bimodules in place of type DA bimodules.)

Involutive Floer homology

bfh_python can compute the dimension of involutive HF-hat of a 3-manifold Y. Decompose Y as a union of two handlebodies H1∪H2 (which we view as bordered 3-manifolds). There are some special Heegaard diagrams AZ and AZ-bar, with the property that gluing AZ to AZ-bar gives a Heegaard diagram for the identity cobordism. Then the involution of CF^(Y) is the composition

CFA(H1)⊗CFD(H2)→ CFA(H1)⊗CFDA(AZ)⊗CFDA(AZ-bar)⊗CFD(H2)→ CFA(H1)⊗CFD(H2)→

where the first map comes from homotopy equivalences

CFA(H1)≃CFA(H1)⊗CFDA(AZ)
CFD(H2)≃CFDA(AZ-bar)⊗CFD(H2)

and the second map comes from the homotopy equivalence CFDA(AZ)⊗CFDA(AZ-bar)≃A(F). It is relatively easy to write down the latter homotopy equivalence explicitly. The former homotopy equivalences turn out to be unique up to homotopy. (This uses the fact that the Hi are handlebodies.) So, to compute the involution underlying involutive HF-hat, bfh_python simply searches for some homotopy equivalences of the specified form.

This algorithm is much less well optimized (and hence slower) than the rest of bfh_python. In particular, this last search for homotopy equivalences could likely be improved substantially.

Gradings

The gradings in bordered Floer homology are somewhat unusual. The dg algebra A(F) is graded by a noncommutative group with a distinguished central element. In fact, there are several useful choices for the grading group. One is a ℤ central extension of H1(F), corresponding to the intersection form on H1(F). We call this the small grading group and bfh_python uses the class SmallGradingGroup for it. Another is obtained by extending this group to the corresponding ℚ central extension of H1(F;ℚ). This comes up implicitly in bfh_python when one chooses the option use_rational in grading computations (e.g., in SimpleDbGradingSet().eltEquals()). A third, the big grading group, is a ℤ central extension of ℤ4g-1; the corresponding bfh_python class is BigGradingGroup.

The bimodule associated to a cobordism from F1 to F2 is graded by a set S with a left action by the small grading group of F1 and a right action by the small grading group of F2. Tensor products of (bi)modules correspond to mixing the corresponding G-sets (that is, taking the product and then quotienting by the group actions where the tensor product was performed).

The result, for a closed manifold, is a grading by a ℤ-set. This is the structure one expects: a partially-defined, relative, possibly cyclic grading. This corresponds to the grading of Heegaard Floer homology by vector fields or 2-plane fields (cf. Kronheimer-Mrowka's book or the work of Gripp-Huang). Working with the extension to ℚ also computes the relative rational grading between generators whose spinc-structures differ by a torsion element.

References

For a longer survey of bordered Floer homology, see:

  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, A tour of bordered Floer homology.

Computations of the bimodules needed to compute HF-hat of 3-manifolds and to compute Ozsváth-Szabó's spectral sequence for the branched double cover are given in:

  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Computing HF^ by factoring mapping classes.
  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Bordered Floer homology and the spectral sequence of a branched double cover I.
  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Bordered Floer homology and the spectral sequence of a branched double cover II: the spectral sequences agree.

Basics of bordered Heegaard Floer homology are explained in detail in:

  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Bordered Heegaard Floer homology.
  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Bimodules in bordered Heegaard Floer homology.

The notion of local type DA structures is explained in Zhan's thesis:

More about arcslides can be found in:

  • Jørgen Ellegaard Andersen, Alex James Bene, and R. C. Penner, Groupoid extensions of mapping class representations for bordered surfaces.
  • Alex James Bene, A chord diagrammatic presentation of the mapping class group of a once bordered surface.

More versions of the pairing theorem, and discussion of the diagrams AZ and AZ-bar are in:

  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Heegaard Floer homology as morphism spaces.

The algorithm for computing HFI^ using bordered Floer homology is in:

  • Kristen Hendricks and Robert Lipshitz, Involutive bordered Floer homology.

Helpful examples for working with the gradings can be found in Section 11.9 of Bordered Heegaard Floer homology, as well as in:

  • Robert Lipshitz, Peter Ozsváth, and Dylan Thurston, Relative ℚ-gradings from bordered Floer theory.