
Directional emission from deformed dielectric resonators has turned out to be one of my most influential discoveries over the past decade.
More information on this topic can be found in my discussion of microdroplets, where the paper cited above is explained further. The reason why I think that paper is so important is that it combines a ray-based way of thinking with numerical wave calculations and experiments. The successful integration of these approaches is crucial in order to overcome the knee-jerk aversion that some pure computational physicists in electromagnetic research had (and still have) to ray approximations.
My earliest work on directional emission was purely theoretical; this is an example where theory actually gave rise to new experiments which had not been attempted previously. This page describes only the theoretical starting point.
My wave simulation of the Robnik (or Limaçon) billiard was first posted online in 1997, see this Internet Archive entry from 1997, and the screen shot of my very "nineties" looking web page back then.
The emission directionality of the well-studied Robnik
billiard conforms well to the classical prediction we made in
Opt. Lett. 19, 1693
(1994).
The citation for the results on this page is
Jens. U. Nöckel, Poster presented at the German-Israeli Meeting of Young Researchers: 26 - 27 June 1997, Max-Planck Institute for Physics of Complex Systems, Dresden (Germany).
I thought it's worth adding these comments about my original studies here because directional emission from this same model system is still being studied more than ten years later.
This is just one of the many laser resonator shapes for which I have studied the emission directionality. The Optics Letter cited above is my first paper on the quality factor and emission directionality of microlasers. It states a ray-based formulation of the main ideas which I subsequently corroborated using numerical wave simulations such as the one on which the false-color plot below is based.
I call this particular shape the Robnik billiard because Prof. Marko Robnik's previous studies of quantum chaos in billiards of this shape made them a great test case for our methods. Whatever name you prefer, mathematically this shape is parametrized in polar coordinates by r(φ) ∝ 1 + ε cosφ where φ is the azimuthal angle and ε the fractional deformation from circular shape.
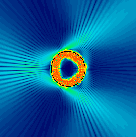
 Shown here is the Robnik billiard at
fractional deformation 0.045 and refractive index n=2. The
wavenumber on the outside is kR=43.1 (R is the undeformed
radius), corresponding to kR=86.2 on the inside. The
resonant state depicted here corresponds to classical rays
for which the angle of incidence χ with respect to the
surface normal roughly satisfies sin χ=0.7.
Shown here is the Robnik billiard at
fractional deformation 0.045 and refractive index n=2. The
wavenumber on the outside is kR=43.1 (R is the undeformed
radius), corresponding to kR=86.2 on the inside. The
resonant state depicted here corresponds to classical rays
for which the angle of incidence χ with respect to the
surface normal roughly satisfies sin χ=0.7.
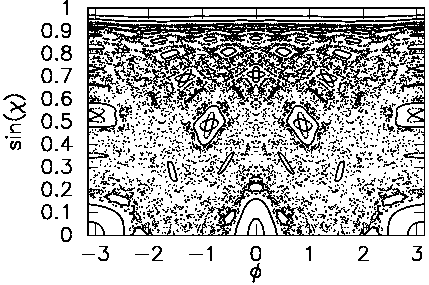
Such rays lie in the chaotic region of phase space. One sees tangential escape from the high-curvature regions. The Poincaré section (right) of the Robnik billiard at this deformation shows the extent of chaos and island structure.
Directional emission as a consequence of chaotic diffusion in ray phase space has been studied not only in two-dimensional model systems (though two-dimensional optics is indeed of great technological relevance, see the Hitchhiker's Guide to microlasers). An important type of optical microcavity that provided a crucial experimental testing ground for our theory are (three-dimensional) spheroids, in the form of droplets and also glass beads.
This page © Copyright Jens Uwe Nöckel, 06/2003
Last modified: Mon Jul 11 10:34:21 PDT 2011