10. 复杂周期波形
傅立叶分析,以十九世纪法国数学家让·巴普蒂斯·约瑟夫·傅立叶的名字命名。傅立叶分析可以将复杂周期波形划分成基本的不同频率,振幅以及相位的正弦波分量。相反的方法,将不同频率,振幅以及相位的正弦波相叠加组成复杂周期波形的方法,叫做 傅立叶合成。
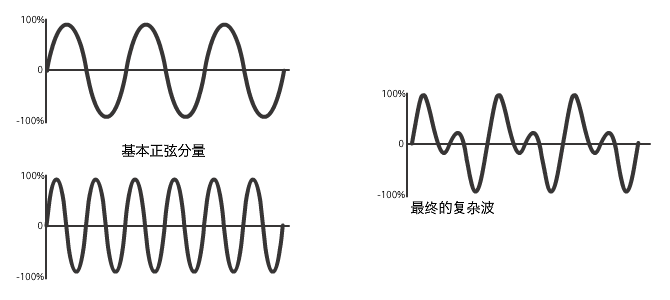
复杂波形便是将两个或者两个以上的正弦波瞬时振幅相叠加的结果。
范例 10-1: 傅立叶合成,将不同的正弦波形相叠加,形成复杂波形。
有些时候,相叠加的波形振幅相互加强得到更强的振幅。这种情况叫做 相长干涉。有些时候,波形叠加得到振幅的消减,这种情况叫做 相消干涉。
与最终复杂波形相同的周期的频率叫做 基音频率,或者基频。基频永远都是一个复杂波形当中最低的频率分量。高于基频的频率分量叫做 分音。
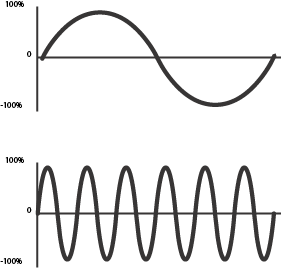 基频
分音
基频
分音
图表 10-2: 基音频率和分音频率。