
All images on this page (plus the wave and Husimi plots in the Science article, and including all the color plots now being found in various news releases) have been created by me with computer programs which I wrote mainly at Yale University, but then significantly improved at the Max Planck Institute for Physics of Complex Systems. The exact solutions of the wave equations for deformed dielectric resonators, of which the above pictures are an example, are calculated using the Max Planck Institute's DEC Alpha computers.
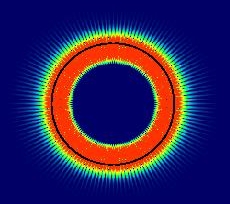
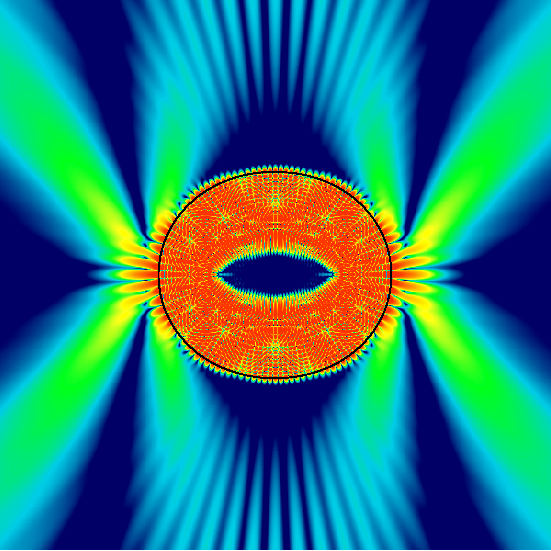
Although high intensity (red) can build up in the resonator, there is no preferred escape direction, and in fact leakage is very small because it can only take place by quantum-mechanical tunneling through the barrier made up of the jump in refractive index between inside and outside region. The inside is a semiconductor with refractive index n > 1, the outside is air with n=1. The waves are squeezed toward the interface (indicated by the black circle) - this can be visualized as the result of a centrifugal force acting on them as they rotate around. This picture assumes n=2 in the circular cylinder. In the new Bell Labs experiment, an important role is played by the larger value of n=3.3, because larger n means better confinement of the light. That would make it even more difficult for any rays to leak out if they were following a similar whispering-gallery pattern. On the other hand, better confinement is also the prerequisite for getting lasing out of the bowtie mode, see below. This is why the bowtie takes over and does all the work soon after it is born in a bifurcation (i.e. a chaos-induced instability tantamount to the tearing-apart of a more well-behaved, regular ray pattern existing at smaller deformations).
To download the manuscript of the Science article, please choose High power directional emission from lasers with chaotic resonators.
The published article has a small error in it, which was corrected in a
Letter by Claire Gmachl [Science 282, p.47 (1998)]:
The deformation of the resonator shape at which the bowtie mode ceases to
be a stable periodic orbit was given as eps= 0.23
(for a definition of eps, see below). The correct upper limit for the
deformation parameter to create a stable bowtie mode is eps =0.18,
as was pointed out to us by Anthony E. Siegman. None of our findings are
are affected by this error.
Signature of Dynamical Localization in the Lifetime Distribution of Wave-Chaotic Dielectric
Resonators
Authors: Oleg A. Starykh, Philippe R. J. Jacquod, Evgenii E. Narimanov , A. Douglas Stone
Abstract:
We consider the effect of dynamical localization on the lifetimes of the resonances in open wave-chaotic dielectric cavities. We show that
dynamical localization leads to a log-normal distribution of the resonance lifetimes which scales with the localization length in excellent
agreement with the results of numerical calculations for open rough microcavities.
We are considering the "flatty" shape. In actual units , we write the cavity shape as
r(phi)=R * Sqrt[1 + 2*eps* Cos(2 phi)].
Here, R has the dimension of length, e.g. in microns.
The experimental shape has a fixed short diameter of 50 microns, i.e. at
phi = pi/2 one has to set
R Sqrt[1 - 2 eps] = 25 microns.
The emission wavelength is approximately 5.2 microns, and is related to
the size parameter by
kR = 2 Pi R/lambda = 2 Pi * 25 microns / (Sqrt[1 - 2 eps] * 5.2 microns).
This implies at eps = 0.06
kR = 32.2,
and at eps = 0.15
kR=36.1.
The spectrum of this shape at eps=0.15 is shown below. Note that I am showing a
spectral interval at about twice the frequency as the experiment. The states
with the experimentally relevant frequencies are treated in the paper, and
will be discussed further below.
The fact that the results are essentially the same for the much higher-energy
states shown here just serves to show that frequency does not matter much
when we look at phenomena that have a clssical origin. This is the case for
the emission directionality of these states, as well as for the resonance
widths ! This latter fact is explained in our
Nature paper, where it is argued
that the linewidths on the wavenumber axis will be the same for all resonances
that are semiclassically quantized on the same portion of the classical phase
space, provided that the dominant escape mechanism is a classical process
such as phase space diffusion.
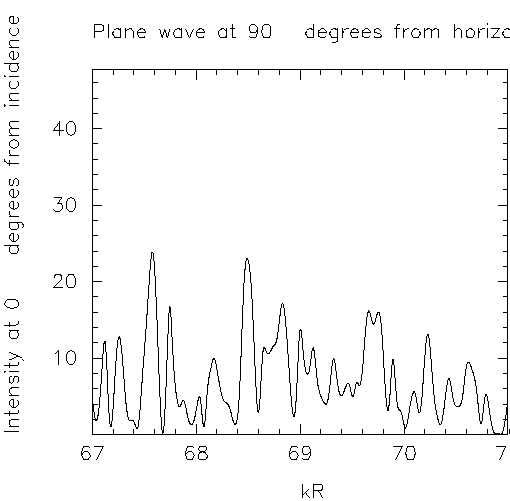
Most of the resonances are too broad to support lasing. What is the origin of the sharper features ?
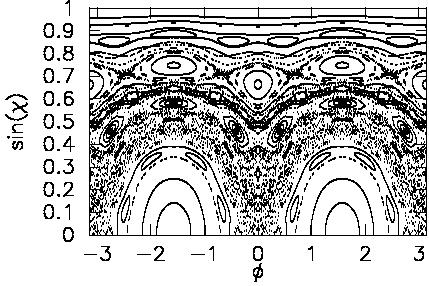
Look at the classical phase space portrait (surface of section, or
SOS) for eps=0.15,
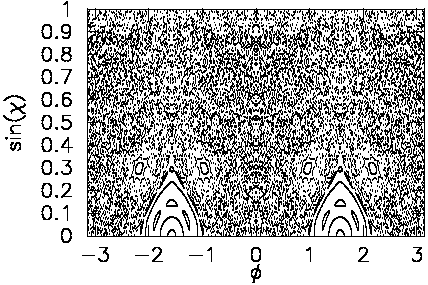
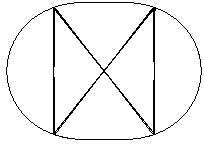

Its directionality is shown here (eps=0.15).
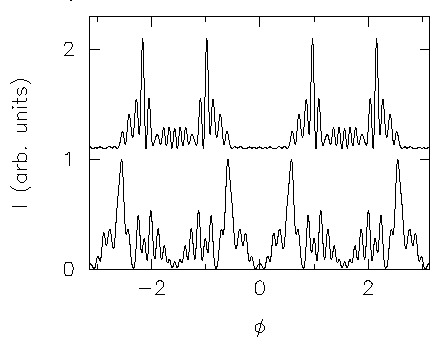
In all directionality plots, the top panel is the near field and the bottom
shows the far field intensity.
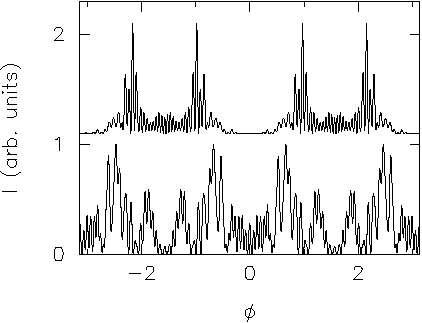
As we can already see from the wave function, the ribbon making the bowtie is actually broader than could be supported by the island itself. To show where in phase space this state is located, look at the Husimi plot.
A Husimi plot is a representation of the wave field as a probability distribution in the classical phase space. It is obtained by forming the overlap between the wave function and a minimum-uncertainty wave packet centered at the given classical coordinates.
Here I show the Husimi plot superimposed with the corresponding SOS:
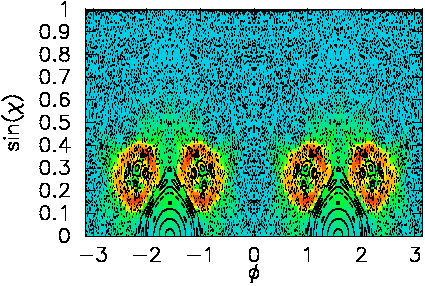
The rays are sticking to the neighborhood of the bowtie- and to a lesser extent also to the mainbouncing-ball island.
In making this plot, I did not use a logarithmic scale, but took a square root
of the function to enhance smaller values close to 0.
To enhance small Husimi weight even more, here I raise the function
to the power 1/4, and plot only the stable islands, not the chaos, so as
not to obscure the Husimi plot:
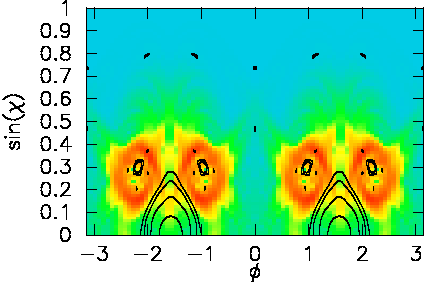
Let us first check if such a state retains its bowtie character when eps is
lowered. After all, there are clearly many anticrossings, and especially at
smaller eps below eps=0.133 we cannot trust this to be the correct state.
Here is the wave function for eps = 0.134:

It becomes more difficult to distinguish this from a pure bouncing-ball orbit.
The directionality looks like this:
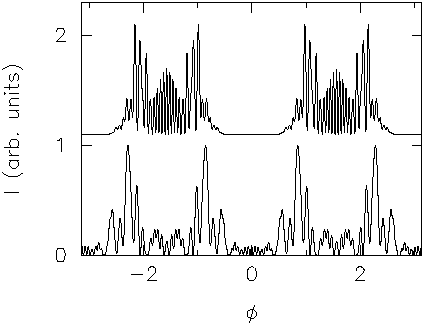
It also becomes more similar to that of the bouncing ball orbits existing at the same deformation. Of course, so does the resonance width, which increases.
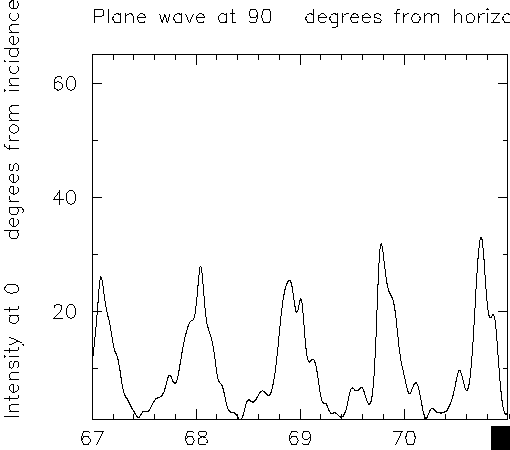
The dominant mode spacing is that of the bouncing balls, approximately
given by pi/n.
Here is the SOS:

The directionality is shown here:
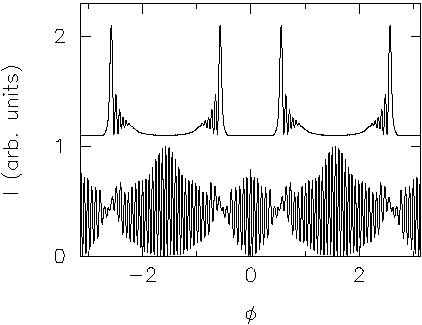
Clearly, this is a much less directional emission. The envelope shows broad peaks, but its minima are not very deep, i.e. they don't go to zero, only to 1/2 of the maximum envelope.
The wavenumbers used so far are twice those actually present in the experiment. This shows the power of classical arguments, allowing us to infer features of the wave solutions that are valid universally in different spectral ranges, by comparing to the results at the experimental wavenumbers.
This will be done now, keeping the deformation at eps=0.06 for now.
Here is the corresponding spectrum,
showing a rather similar dominant mode spacing as before.
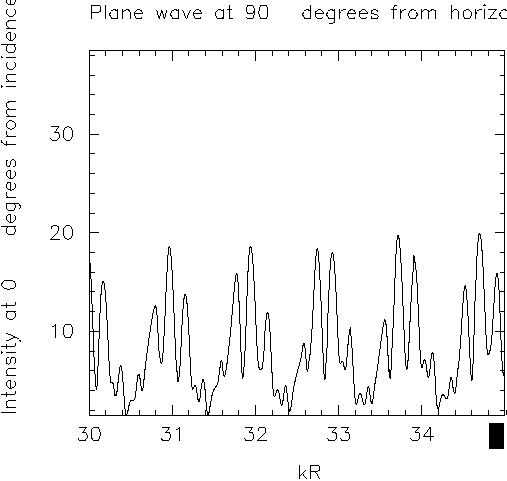
Whispering-gallery states
At k=33.61, there is a resonance of width gamma=7*10^(-4) which shows
up in the spectrum as a tiny spike (consisting of one data point,
which hence is invisible in the above image).
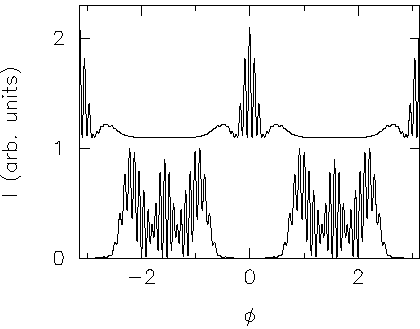
Here is its wavefunction:
The directionality is still rather broad, although the envelope has
intervals where it vanishes.
To see where in phase space this function is localized, consider the Husimi
plot:
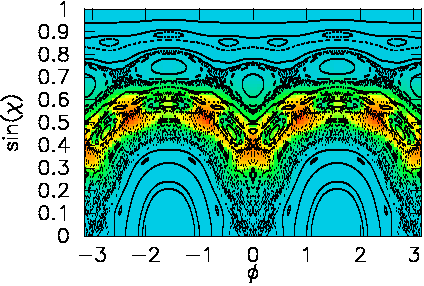
The Husimi density beautifully follows the chaotic layer roughly up to
tangency to the critical line for escape. The 6 islands corresponding to the
triangular orbits are clearly avoided. Also note the 8 islands, the lowest
of which is centered at phi=0, sinchi=0.25 in the SOS. The latter
causes partial dynamical eclipsing (as opposed to a total eclipse),
which explains why the directionality shows the combination of tangential
escape and split peaks in the far field. Here is the shape of the orbit
responsible for the eclipsing:


The Husimi plot is shown here:
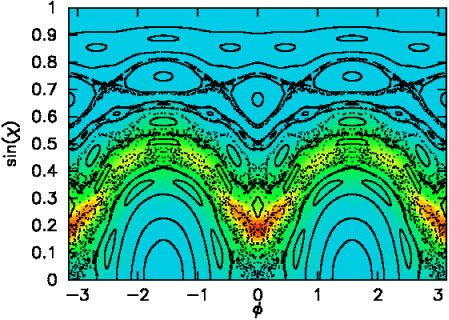
The directionality is shown here:
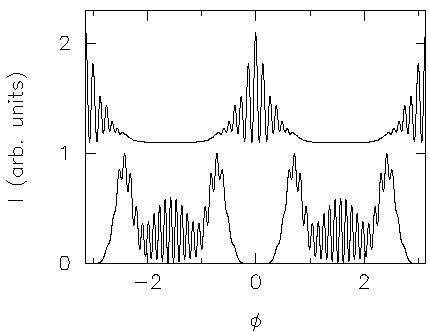
A bowtie state at deformation eps=0.15 and wavenumber
kR=35.83 and gamma=0.043 (i.e. Q=833) is shown here. It is
different from the one used in the Science article:

The unsmoothed directionality is shown here:
Here is the Husimi plot.
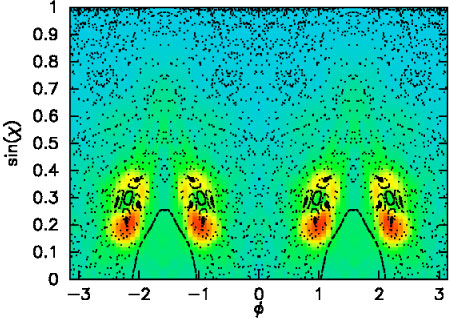
Interestingly, the state is not localized on top of the bowtie islands, but instead surrounds it almost like a halo. The question is: is this due to dynamical localization or does the ray simply escape before having a chance to diffuse far away from the "sticky" region near the islands ?
| Related information is found on the following web pages: |
This page © Copyright Jens Uwe Nöckel, 06/2003
Last modified: Mon Dec 27 18:13:27 PST 2010