Reading: Chapter 2

Introductions Course Home Page Let's not forget our joke Science is a process Inertia Intro to Motion

Inertia

Aristotle

The ancient Greeks thought about how objects move and forces that act upon them. Aristotle (384-322 BC) was one of the more famous Greek philosophers. One outcome of Aristotelian thinking is that an arrow, when shot ("violent motion"), has a force acting upon it until it comes to its "natural state" (at rest). Clearly the shooter of the arrow can't exert a force on it once the it leaves their bow, unless one considers forces acting at a distance, such as gravity and electrical forces. Even today many people would argue that an arrow in motion must have a force acting on it that causes it to move (but not to slow down), and that the force is used up as the arrow slows down.

Galileo

The Italian Galileo Galilei thought differently... and paid the price for it! For one, he advocated for the Copernican view that the sun was at the center of the solar system, which went against church dogma. He was tried for this view and forced to renounce his discoveries.

One of Galileo's discoveries involved balls rolling down ramps, along level tracks, and up ramps.



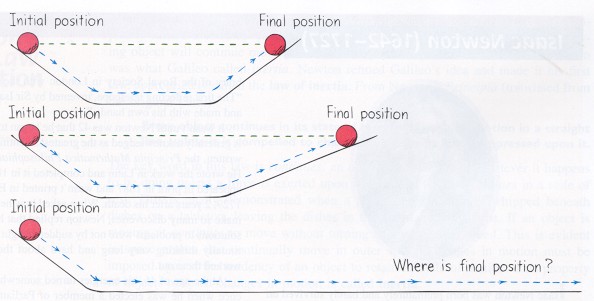
A ball rolling down a ramp would roll on the level and up another ramp, coming to more or less the same height as it started (he recognized that friction prevented it from reaching the same height).

Galileo found that he could make the end ramp longer and less steep and the ball would return to the same height regardless. He reasoned that an end ramp that was almost level and quite long would result in the ball rolling on, seemingly forever.

This property of the ball-- to roll on forever without changing speed along the level track-- he called inertia.

Newton

In 1642, when Galileo died, Isaac Newton was born in England. By the time Newton was 23 he had developed his three laws of motion. His first law included Galileo's findings about inertia for moving objects:

Every object continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.

Newton's first law allowed for a state where an object was at rest. It also very carefully described uniform motion to be in a straight line, without change in speed.

How does one change the state of uniform motion, or of rest, of an object?

Apply a force!

So INERTIA tells us something about an object's tendency to stay in the same state (say, Nebraska, for example). It could be at rest, or moving at a constant velocity (speed and direction).

What are some important characteristics controlling inertia?

"Net" Force

Aristotle's arrow does have a net force acting on it, even after leaving the archer's bow. Air resistance causes it to slow down.

It is useful to think of the forces acting on the arrow in terms of components. Air resistance (drag) acts in the horizontal direction, opposite the horizontal direction of travel of the arrow (to the right, below).

• After release, this is the only horizontal component of force acting in the horizontal direction.



• Both air resistance (up) and gravity (down) act on it in the vertical direction.

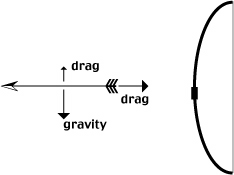
{The vertical component of drag begins to act on the arrow only after the arrow begins to fall. The faster the arrow falls, the greater the drag, so the upwards pointing drag arrow (above) grows over time.}

Does the horizontal drag force change over time? Does the gravity component of force? can the vertical drag arrow grow larger (greater) in size than the gravity arrow?

• We say that the arrow has a (non-zero) net force when the sum of all forces (in a given direction) is not zero.
• This net force could serve to change an object's state-- from resting to moving, or from moving to resting. If there is no net force in a direction, an object won't change its state of motion in that direction.

It is possible to have two forces acting on an object with no resulting net force. Think of equal strength forces acting in opposite directions on an object. So forces add together like vectors: arrows whose length shows strength and whose direction shows, well, direction!

One can also arrange to have two forces that add together or subtract, but result in a non-zero net force acting on an object. This will change that object's state: if it is moving, its motion will change (speed, direction), if it is still, it will begin moving.

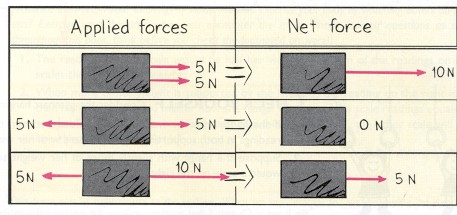
What would the vectors (arrows?) representing horizontal forces on our archer's arrow look like through the arrow's launch and flight? Would the net horizontal force on the arrow be constant throughout?

Equilibrium

As stated above, it is possible to have two forces acting on an object with no resulting force. The arrows representing the forces are equal in length and opposite in direction. Or there are no forces acting (in a direction) at all! We represent this by the symbols:

SF = 0

The "S" means "sum of" and F represents force. This says that the sum of forces is zero. In writing this we usually refer to forces in the same straight line (e.g. horizontal, or vertical). To make this more explicit, we put a subscript on the F to denote the direction we refer to (say "h" for horizontal):

SF_h = 0

This condition is known as mechanical equilibrium.

An object in mechanical equilibrium won't change its state, be that resting or moving at a constant velocity.

Things that are moving

An object in constant motion is also in equilibrium.

Equilibrium is a state of no change.

When is the archer's arrow in mechanical equilibrium? When is it not?

If an object is moving at a constant velocity (in equilibrium) then either no forces are exerted on it, or all forces (in a given line) add to zero. Here's an example.

Introduction to Motion- Position, Velocity and Acceleration

For now, let's confine ourselves to motion in a straight line, or one-dimensional motion. The system we observe is some object in motion. We wish to:

describe that object's motion as completely as possible.

use descriptive characteristics (variables) to do so.

we already know a little about mass

we think we know about forces, though there's more to come.

what are some other variables useful for describing motion?

• figure out a relationship between those variables (are mass and velocity 'going steady?')
• test our relationship, fix it up if necessary.
• build up a grand "theory" of motion.

Useful variables- Part One:

Let's say our object in motion is the instructor's private jet (I wish...), taking him home after a hard day of teaching. How do we describe the instructor's position at a given time after leaving UO?

Distances & displacements or, "where's Crow, Oregon?"

• 

• Note that specifying a distance requires knowing the starting point and how far you went from there.
• Specifying displacement requires knowing two positions:

  start point

  end point

• Knowledge of displacement entails knowing about a change in position. This means knowing how far apart the two points are (distance) and, also, the direction from start to finish.
• So our (incomplete) list of important variables now includes displacement.

• And since we're thinking about motion, we figure that time must also be important.

• Let's practice making position vs. time graphs.

  ---

• Useful Variables- Part Two:
• What about speed & velocity? Let's speculate that:

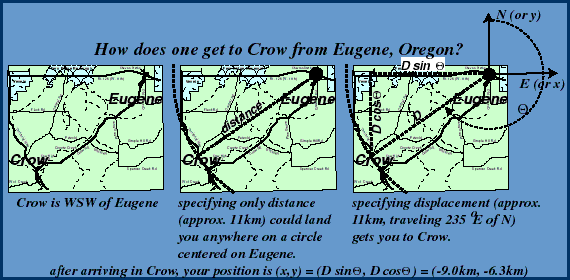
  Speed-- distance (traveled) over time (which wounds all heels?).

We can test our hypothetical relationship between speed, distance and time by making, matching and interpreting graphs of distance vs. time.

standing still (what is the speed?)
moving away from detector quickly (what is the speed?, velocity?)
moving away from detector slowly (what is the speed?, velocity?)
moving towards detector slowly (what is the speed?, velocity?)
"velocity match"

What can we say about the motion associated with different segments of our position-time graphs?

Do our experiments verify the above relationship between speed, position and time?

Definition:

average speed is the distance traveled (d here) over the time elapsed, t.

A refinement of the relationship: Speed and velocity-- what's the difference?

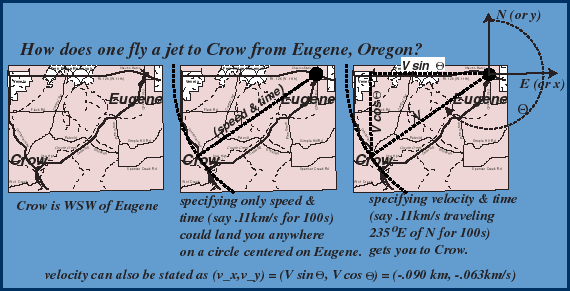
Definition:

average velocity is the change in position (Dp here) over the change in time, Dt (which is the time elapsed).

Note that f stands for final, and that i stands for initial. So that our velocity over some interval of time is the final position minus the initial position divided by the final time minus the intial time.

• Aside: Just like forces, velocities are vectors, and can be represented by arrows. To carefully specify velocity, one needs to know both its magnitude (length of arrow) and its direction. We typically keep track of the change in position in three direction (dimensions; Dx, Dy & Dz or, perhaps, east, north and up). We can then calculate the three velocity components (v_x, v_y, v_z) that describe our arrow, just like the horizontal and vertical components of force described how our hanging weight was held up, above. This gives a complete description of our velocity.

standing still
moving away from detector quickly (how does it compare to position vs. time?)
moving away from detector slowly
moving towards detector slowly
velocity match

Next Lecture Back to Course Page.