Essentials of Physics- PHYS 101

Lecture 2 / Lecture 3

Reading: Chapter 3, pages 40-44, Chapter 4, pages

A Recap about Inertia

How does one judge the difference in weight (or better yet, mass) between two similar object? It's called hefting. What characteristic of the objects are you testing when hefting?

solar observation handout

Recycled humor

Velocity recap.

Changing velocity but not speed.

Acceleration.

ILD1: Different acceleration and velocity graphs.

Using acceleration to determine velocity and position.

Break

Joke of the day 2.

About that ILD earlier.....

Acceleration to tell how fast and how far.

The relationship between acceleration and force.

Problem-solving tricks and techniques

Newton's Second Law

Class Business-- Solar Observations

By now you should have received your acrylic half-domes and the instruction sheet for solar observations. Solar observations are to be recorded for 2 different, sunny days. Try to complete the first day's observations as soon as possible. Separate your observations by at least two weeks, if not more. Use the same dome for both sets of observations. Mark the domes with different colored pens to denote each day.

Observations, including the completed instruction sheet and dome, are due at the beginning of Lab 6, on May 10th or 14th.

Here is the PDF file of the instruction sheet.

Introduction to Motion- Position, Velocity and Acceleration

Useful variables- Part One:

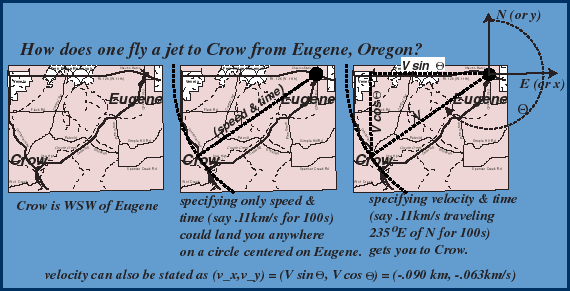
Let's say our object in motion is the instructor's private jet (I wish...), taking him home after a hard day of teaching. How do we describe the instructor's position at a given time after leaving UO?

Distances & displacements or, "where's Crow, Oregon?"

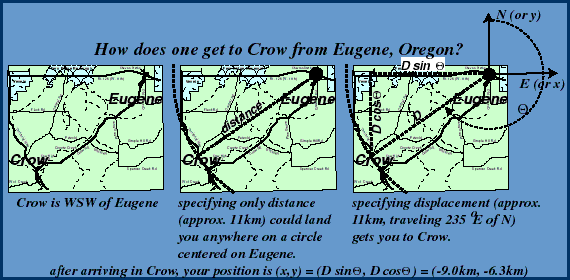
Knowledge of displacement entails knowing about a change in position. This means knowing how far apart the two points are (distance) and, also, the direction from start to finish.

So our (incomplete) list of important variables now includes displacement.

And since we're thinking about motion, we figure that time must also be important.

Let's practice making position vs. time graphs.

Useful Variables- Part Two:
What about speed & velocity? Let's speculate that:

We can test our hypothetical relationship between speed, distance and time by making, matching and interpreting graphs of distance vs. time.

Let's make some speed vs. time graphs (joy, o' joy!)!

In particular, graphs of:

Further Questions:

Definition:

average speed is the distance traveled (d here) over the time elapsed, t.

 

A refinement of the relationship: Speed and velocity-- what's the difference?

Definition:

average velocity is the change in position (Dp here) over the change in time, Dt (which is the time elapsed).

Aside: Just like forces, velocities are vectors, and can be represented by arrows. To carefully specify velocity, one needs to know both its magnitude (length of arrow) and its direction. We typically keep track of the change in position in three direction (dimensions; Dx, Dy & Dz or, perhaps, east, north and up). We can then calculate the three velocity components (vx, vy, vz) that describe our arrow, just like the horizontal and vertical components of force described how our hanging weight was held up, above. This gives a complete description of our velocity.

Let's make some velocity vs. time graphs (joy, o' joy!)!

In particular, graphs of:

Changing velocity but not speed.

Well... can we? If so, how? Can we change speed without changing velocity?

Useful Variables- Part Three:

What about acceleration? We define it to be related to velocity vs. time graphs.

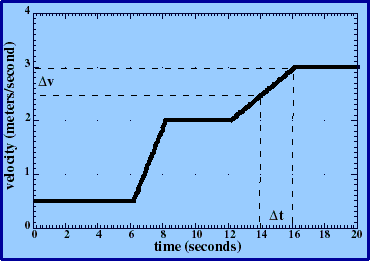
Definition: average acceleration is the change in velocity over the time elapsed.

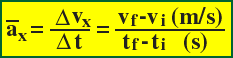
Questions:

    • How does acceleration relate to a velocity versus time graph (above)?
      • Challenge: Can you move to match an acceleration graph?
    • What does negative acceleration look like on a velocity-time graph, what does it "feel" like?
    • Does acceleration have a direction?
    • Can you travel at a constant speed but have an acceleration?

 

ILD: Different kinds of acceleration and velocity.

Acceleration to tell how fast and how far.

Acceleration tells us about change in velocity. If our initial velocity is zero, then acceleration can tell us our velocity after some time using the simple relationship:

velocity acquired = acceleration x time

How Fast

Say you just ran off the end of a cliff, and plan to descend for 5 seconds before hitting the valley floor with a little puff.

In the several moments while you wait to fall (just kidding!) you estimate how fast will you will traveling when you hit:

See, isn't physics useful!

In fact, Wile E Coyote will be travelling 10 m/s after 1 second of fall, 20 m/s after 2, 30 m/s after 3 seconds, and so on.

{note: we are ignoring the force of air resistance, which will oppose his fall and, eventually, equal the force of gravity exerted downwards on Wile (what does that tell you about the air resistance force's relationship to speed?). When this happens, Wile has reached terminal velocity and won't speed up any more (lucky guy!)}

Movietime!

  • "Absolutely riveting!," Rosie (the) Riveter, Steel Structure Journal.
  • "A fascinating juxtaposition of concepts and graphics with, well... ideas and graphs," Sir Oliver Stone-Lb, Royalty Weekly.
  • "A plaintive dynamic cart defying a pushy professor while retaining its pride and dignity-- a lifelike triumph of reality and algebra over style and ignorance," Prof. Livelybrooks, The Extremely August Journal of Physics and Movie Review.

Acceleration to tell how far.

See, isn't physics useful!

How Far

Our average velocity during that time is just 1/2 of the final velocity .

average_velocity = (initial_velocity + final_velocity) / 2.

We also know that average velocity is:

average_velocity = position_change / time.

We can use these three pieces of information to state that:

distance = 1/2 x acceleration x time x time

You ran off the end of a cliff, but don't know how far you will fall. How far will you travel (ever downward!) after 5 seconds of falling?

The relationship between acceleration and force.

Let me guess:

    • they're brother and sister.
    • they've been carrying on for years now... its scandalous!
    • they're frosty just now, acceleration was seen in public snuggling up to mass.

In physics, a "relationship" refers to how one varies when the other is changed. Say we double the total force acting on an object. What will happen to its acceleration? Will it half, stay the same, double, quadruple, or something else?

Here is a graph showing various possible relationships between acceleration and force:

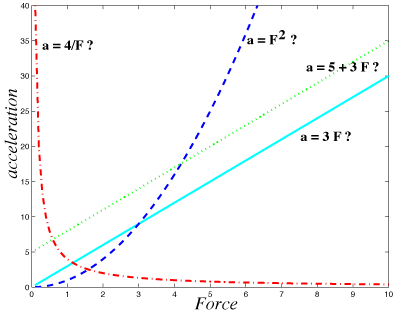
Which of the above mathematical relationships do you think will apply to force and acceleration? Why?

Now that we have predicted (hypothesized) a particular relationship, how do we test it?
Thinking about it another way, if the following velocity-time graph is observed for a certain force acting on a cart, how will that graph change when the force is doubled?

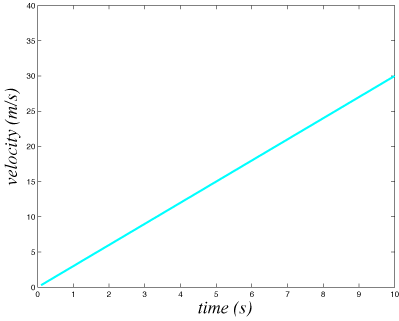
We can test this using our old friends the cart, track, motion detector and, introducing the fabulous hanging mass

  Problem-solving tricks and techniques

Problems solving problems?

1) You can always multiply by 1

    Example: 1.6 km = 1 mile. 1.6 km / 1 mile = 1. To convert miles to km, I multiply by 1:

    8.0 miles x (1.6 km / 1 mile) = 12.2 km

2) Multiply both sides of an equation by the same thing (number):

    Say we know that SF = m a

    Say we also know a and SF. How do I solve for m?

    Multiply both sides of equation, above by the same thing (1/a):

    SF (1/a) = m a (1/a) => m = SF/a

More on the relationship between a, m, and F

 

Last week we observed that the acceleration of a cart doubled when the force pulling it was doubled.   More generally we found that acceleration is proportional to the net force.

a µ F

 

What about mass?

 

We know mass gives an object inertia which resists a change in motion.  Another way to say this is more mass makes an object harder to accelerate.

What is the exact relationship between acceleration and mass?

In lab you kept the pulling force constant but changed the mass of the car.  What you found (hopefully) was that if the mass of the car doubled the acceleration was reduced by half.

 

a µ 1/m

 

'acceleration is inversely proportional to mass'

put all this together to get-- Newton's Second Law

Put this together with a µ F and what do we get?

a = Fnet/m  more commonly written as:   Fnet = ma !

But Dean, I checked F = ma in lab and it didn't work!

Previous Lecture Next Lecture Back to Course Page.