Practice Multiple-choice Problem joke Weigh the Earth Weightlessness Solar System Formation Projectile Motion Circular Orbits Elliptical Orbits Work-Energy Relationship for Satellites Practice Multiple-choice Problem
If you balance a broom horizontally on one finger, the center of gravity of the broom will be above your finger - closer to the bristles end than the handle end. If you saw the broom in two pieces at that point, and weigh the two parts on a scale, you'll find that the heavier part is the:
- bristles part.
- handle part.
- both weigh the same.
Weigh the EarthSo let's solve this equation (Law) for m2. First multiply both sides by d2. Then divide both sides by m1 and G, leaving:
WeightlessnessThose astronauts floating around in the space shuttle. They're just too far from Earth to be significantly affected by its gravity, right?
NOT!
Say that astronauts are orbiting the Earth at about 200 miles (320,000 meters) above the surface. The Earth's radius is 6,370,000m, so the astronauts are 6,690,000 meters above the center of the Earth.
The increase in distance from the Earth's center is:
What about when we drop or accelerate upwards in an elevator?
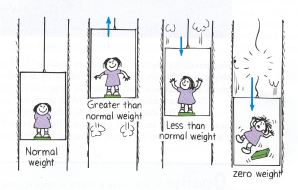
What does Newton's Law have to say about these situations?
Solar System FormationSolar systems are though to form from slightly rotating balls of interstellar gas:
Gravitational attraction between individual gas molecules causes the ball to contract (a).
Conservation of angular momentum (remember walking towards the center of the merry-go-round?) causes the ball to rotate faster (b).
The faster rotating molecules cause the ball to flatten into a disk (c).
Because the disk has greater surface area, the molecules cool and condense.
Condensation into swirling eddies can give rise to proto-planets.
Projectile Motion
Suppose you roll a ball along a level table so that there is little friction.
- What does the path of the ball look like?
- How far does it travel during 1 second intervals?
- Does it travel further during the second 1-second interval than the first?
Now suppose you drop that ball straight down, off the edge of the table.
- What path does it take?
- How far does it travel during the second 1-second interval compared to the first?
- What is the ball's initial horizontal velocity for this experiment?
Finally, imagine that you roll the ball across the table so that it reaches the edge with some horizontal velocity.
- What path does the ball take from there to the ground?
- How far does it travel horizontally during the second 1-second interval compared the the first interval?
- How far does it travel vertically during the second 1-second interval compared the the first interval?
We call this motion (ball rolling of the end of table) projectile motion. It describes the motion of baseballs, cannonballs, divers at the pool, etc.
Circular Orbits
Timing a throw:
I throw a ball a distance of 40 meters (I wish!) and it leaves my hand travelling horizontally at a distance of 2m above the ground. What was the ball's speed when it left my hand?
At first this seems like a hard problem to figure out. Don't I need to know more, like the time it took for the ball to travel the 40 meters!?
We can determine the time because motion in the vertical and horizontal directions are independent. Vertical motion is governed by gravity, and we can figure that out first. Let's do this.
distance = 1/2 x "g" x t x t
where "g" is our usual suspect and t is time. Since we know the distance the ball falls, we can solve for t:
So the time it takes to fall is 0.64 seconds. What was the ball's (horizontal) speed when it left my hand?
speed = distance / time = 40 m / 0.64 s = 62.5 m/s
A "big-league" pitcher can throw baseballs up to 95 mph. How do I compare?
62.5 m/s x 1 mile/1600m x 3600 s / h = 141 mph !!
OK, so I lied!
Going into orbit:
What if I throw a ball horizontally at 8000 m/s?
Why 8000 m/s?
Well, the Earth is curved after all! It "falls off" about 4.9 m vertically in 8000 m horizontally.
If I throw a ball at 8000 m/s, it travels 8000 meters in the second it takes it to fall 4.9 m (that's half of that 9.8 thing). After a second the ball is at the same distance away from the Earth as when it started.
I can put that ball into orbit! Time to start training.
Elliptical Orbits
What happens if we launch our ball at greater than 8000 m/s? The path the ball would travel would not be tangential to the Earth. Thus Earth's gravity would work to slow it down. It would eventually curve around and start back towards the Earth, speeding up as it goes. The path would form an ellipse.
You may have been told that the Earth's and other planet's orbits around the Sun form ellipses. What are ellipses? What does that mean in terms of their orbital motions?
Ellipses are like circles, only they have two focii instead of one center. In analyzing Tycho Brahe's careful observations, Johannes Kepler recognized that the Sun sits at one of the focii of every planet's orbit.
Aside: how elliptical is the Earth's orbit? Answer: Not very! The ratio of the distance between the two focii to the major axis (the eccentricity) is .017. It is difficult to draw this orbit without it looking like a circle.
Here is a cool site summarizing how projectiles can be launched to become satellites.
Work-Energy Relationship for Satellites
What is the energy situation of a satellite in orbit?
Circular orbit:
- Does its kinetic energy (KE) change as it orbits? Why or why not?
- Does its gravitational potential energy (GPE) change as it orbits? Why or why not?
- What about its total energy?
Elliptical orbit:
- Does its kinetic energy (KE) change as it orbits? Why or why not?
- Does its gravitational potential energy (GPE) change as it orbits? Why or why not?
- What about its total energy?
- What does the force look like on a satellite in an elliptical orbit?
Previous Lecture 
Next Lecture 
Back to Course Page. 
