Our daily joke

Motion in a Circle

Rotational Inertia

Rolling down a hill-ILD

Torque

Motion in a Circle

You and a buddy have accidentally shrunk yourselves to the size of peanuts (happens all the time, eh?) You make your way across your living room and jump onto the platter of a turntable (remember "analog vinyl recording media" that were once used to record music?!).

Your dumb buddy stands at the outside edge of the turntable, and is almost immediately flung up against a nearby book. You wisely move towards the center of the turntable. Why?



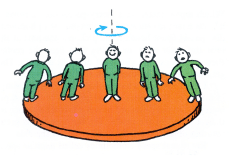
Certainly both you and your buddy make the same number of revolutions per minute regardless of where you stand.

Would we say that you both have the same rotational speed?

(Rotational speed is not the same as linear speed which is what we have been calling speed.)

If an object moves on a circle we can also use the term tangential speed in the same way as linear speed since the direction of the motion is always tangent to the circle.



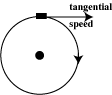
For an object moving in a circle there is a simple relationship between tangential (or linear) speed and rotational speed.

or, in symbols:

v = w x r

So who had the greater tangential speed, you or your buddy who flew off the record? So why did he fly off the spinning record?

Another way to see the difference between rotational speed and tangential speed is to watch a rolling cup.

Every part of the cup must have the same rotational speed, however, the larger end of the cup will have a larger tangential speed. The result is that the wide end of the cup will travel farther than the narrow end in a given amount of time. The cup rolls in a circle.



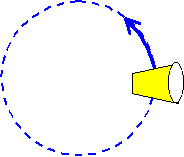
This effect is used to ensure that a train doesn’t roll off of its tracks even when the tracks curve!

Rotational Inertia

We have already studied Newton’s First Law and we learned that every object has inertia which resists a change in its linear motion.

It turns out that a rotating object has a similar property which resists a change in its rotational motion. In a fit of insanity, some rebellious physicist named this property rotational inertia.

Like inertia for linear motion, an object’s rotational inertia depends on its mass. The difference is that rotational inertia also depends on the distance that the mass is from the rotational axis (center of rotation).

Suppose I have a barbell with two equal weights on it. If I grab the bar at the middle and place the weights very close to my hands it will not be difficult for me to spin the barbell about my hand.

However, if I move the weights towards the ends of the barbell it becomes increasingly difficult to twist my hand. When the mass is farther from the axis of rotation it has a greater moment of inertia.

We can calculate an object’s moment of inertia by multiplying every bit of mass times the square of its distance from the rotation axis and adding them together (but I won't ask you to do this....)

For the barbell it looks like this (we will ignore the bar).



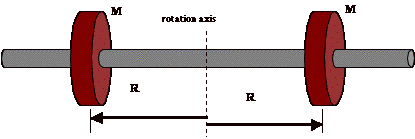
I = M x R x R + M x R x R

I = 2MR²

You can see that moving the masses further from the center increases the moment of inertia for rotation about the center.

Let’s look at some strange ways that rotational inertia affects the way we do things.

• running
• tight rope walking
• balancing a stick

Rolling Down a Hill - ILD

Torque

Why is it harder to hold something at shoulder height with your arm straight than with it bent? The weight of the object certainly doesn’t depend on how close it is to your body.

That is true, but the torque does.

Torque is the rotational counterpart of force.

• Just like a net force will change an object’s linear motion a net torque will change an object’s rotational motion.

Torque is different from force in the same way that rotational inertia is different from linear inertia. Torque and rotational inertia both depend on the distance to the axis of rotation. For torque the distance between the axis of rotation and an applied force is called the lever arm.

Torque = lever arm x force

again, in symbols:

t = r x F

When the net torque on something is zero there will be no change in its rotational motion.

Two children can balance a seesaw when the weight of each produces an equal torque about the pivot in opposite directions (clockwise and counter clockwise). They can do this even when they have very different weights since they can adjust each lever arm (where they sit) to compensate for the difference in the forces they exert.

Previous Lecture Next Lecture Back to Course Page.