Joke of the day. Work and Energy What about Energy? Two Types of Mechanical Energy Work & Mechanical Energy Conservation of Energy Power
How does gravity work?| Let's observe the effect of "gravity" on a softball with the following experimental setup: |  |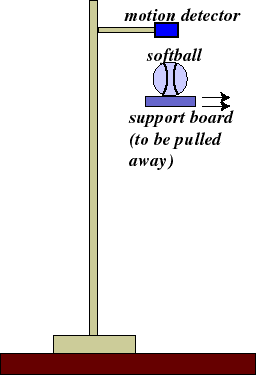
Question: What happens when the board is pulled out from under the softball?
Answer: Duh, let me guess.....
Question: So, HOW is the ball moving towards the ground?
Time for an
Question: If the ball is accelerating, what is causing the acceleration?
Answer: The "force of gravity," the attraction between the Earth and the softball, is causing the ball to accelerate downwards.
Question: Is the "force of gravity" the same for lighter or heavier (less or more massive) objects of a similar shape?
| Try this experiment: |  |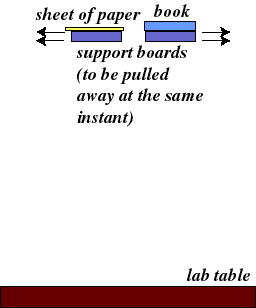
Answer: OK, so they both hit at the same time (after suitable modification). That means that they both accelerated in an identical manner, speeding up towards the table at the same rate.
The Force of Gravity or... Sir Isaac Newton to the rescue!
At the surface of the Earth*: (* technically-speaking, g is observed to vary slightly at different places on Earth. This is because, in part, the surface of the Earth is different distances from its center because of 'equitorial bulge,' mountains, etc. It is also true that differences in the composition of the Earth's crust cause very small changes in 'g.' Geophysicists use careful measurements of 'g' to map differences in structure in the crust.)
The gravitational force that the earth exerts on an object is proportional to the object's mass. So in free fall an object's acceleration is:
Notice that a doesn't depend on mass.
or... Was Aristotle some kind of idiot or what?
What is our every day experience with falling things?
Take paper for instance:
Terminal Velocity (no, not the movie with Charlie Sheen)
Again, what is our every day experience with falling things? The net force acting on a falling object, Fnet, depends on 'gravity' (called W, below), but also on something else we call 'air resistance' (R, below)
This changes (reduces the magnitude of) the acceleration of a falling object. We can substitute into above to get:
Interestingly, air resistance (R, above) depends on velocity. It is zero when an object is at rest and just about to fall. It grows over time as the object falls. Indeed, with sufficient room to fall it will increase until it exactly balances the weight of an object (W, above).
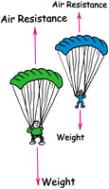Imagine putting your hand out the window of a car as it accelerates. Certainly the faster the car goes the more force the air exerts on your hand. This is because air resistance is proportional to velocity.
We can write it as, R = bv, where b is a number that depends on the how much air an object has to move through (something to do with its shape).
Terminal velocity is reached when Fnet = 0, or when W = R. What can we say about an object's acceleration and velocity when it has reached terminal velocity?
We can solve for terminal velocity in terms of a falling object's mass (m), g, and something called b, which depends on an object's shape:
that's weight divided by "shape
Notice that v DOES depend on an object's mass. So Aristotle wasn't really so dumb. Massive things do fall to Earth faster when air resistance is important.
Work and EnergyThe word "energy" has many, many meanings in every-day usage. In order to compare energy apples to energy oranges, physicists insist on a very precise definition for this word. We define "energy" in terms of "work," so let's start with the latter.
What, specifically, is work? Scientists have a very particular definition for work-- a term that can mean many different things in every day language (e.g., I worked out, I got worked up or, we can work it out.). For simple objects, work is defined as the net force exerted on the object times the distance it is moved:
Work = Force x Distance
In this case, the only important part of a force doing work is that part which points in or away from the direction of of displacement (remember, "displacement" is a distance and a direction).
To make the book move upwards (from rest), he must first apply a force slightly greater than that of gravity, which is pulling down on the book. Over the entire motion of the book the net force he applies must be equal to the book's weight.
Sure he is telekinetically applying a force, but the book isn't moving in the direction of the force. Hence there is no force applied over a distance.... no work being done.
Sure, he may have to apply a force upwards to keep the book from dropping in response to the force of gravity, but that force is perpendicular to the direction the book is moving. So it doesn't count. Before and after moving the book horizontally it is still, and thus hasn't gained any kinetic energy.
Actually, to start the book moving and to stop it at the end does require application of some force in, and then opposite, the direction of motion. While it is moving at a constant velocity tele-man IS doing work on the book, but so is air resistance. So the net work on the book is zero during that part of its motion, positive when the book is starting to move horizontally, and negative when the book is stopped, so that the total work done on the book moving horizontally is zero.
Time for a demonstration!
Does it matter how long tele-man takes to lift the book 1m?
Remember, work is defined as force applied over a distance, NOT force applied over time.
Now what about energy?Definition: Energy is the capacity to do work.
The more work a simple object can do, the more energy it has.
Energy is a description of the capacity to do work, but what "has" energy and what does the work?
However, the "capacity to do work" involves either work being done on the book, or work being done by the book.... work is something that requires interaction with something else.
Two types of mechanical energy: kinetic and potential
Kinetic energy (KE) is energy in motion. If a car is in motion, it has the capacity to do work... by running into something! So KE fits our definition for energy.
- Further, if one object has more mass than another and both move at the same speed, the more massive object can clearly do more work than the lighter one.
- It turns out that velocity matters, also. If two identical objects moving at different speeds run into two, other, stationary identical objects, the object hit by the faster moving object will have the most work done on it.
Potential energy:
When a system gains potential energy (PE), it gains the potential to do work. In lifting a book, I do work on it. It gains potential energy relative to the Earth. When I let go, this PE is converted into KE. For the book, this particular kind of potential energy is called gravitational potential energy (GPE):
Note that an object's potential energy always relates to another object, or other objects. The GPE of a raised book is in relation to the Earth.
Telepathy-man loses his concentration.
Work & Mechanical EnergyIn general, then, work serves to change the energy of an object. Work is not energy, but a way of transfering energy from one object to another. Work is done on or by an object. Energy describes the state of the object, but that can be the state relative to another object.
Conservation of EnergyEnergy is neither created nor destroyed: it is only transformed from one form into another.
POWER
Previous Lecture 
Next Lecture 
Back to Course Page. 
