Essentials of Physics- PHYS 101 Lectures 8/9

A joke a day keeps the doctor away

Review of exam

An Example "Physics in the Real World" Report

Review

Torques

Torques and Simple Machines

Centripital Force

Weigh the Earth

Weightlessness

Gravitational Fields

Projectile Motion

Work-Energy Relationship for Satellites

Review of Exam

Average score for the exam was 17.2 points out of 32, or about 54%. Here is what the grades distribution looks like.

Example "Physics in the Real World" Report

I have observed Physics in the Real World a few times this past week. Here is my report on one simple machine that uses physics to make life easier. You can refer to this as an example of how your first report (if you are doing this sort of report for your first project) should be structured.

Example Real World Physics report: Heavy lifting with the hand truck

Outline of Report:

• Introduction and background (1-2 paragraphs + illustration):
  • Say what is being discussed, how it is used in society, and other interesting things about it. Mention the physics prinicpals (e.g., inertia, prinicple of lever, Newton's Second Law, work & energy, etc.) that are involved.
• How it works and Analysis (3-5 paragraphs + figure/diagram)
  • Go into more detail about how the tool, object or phenomenon functions. Sometimes a step-by-step list is useful. Include a labeled diagram and refer to it. State the specific physics principles involved in both words and as formulas. If your subject is a tool or machine, note in your report how these principles are addressed in its design. If it is something in nature, such as a bird's wing, again note how its "design" follows these principals. Be sure to include a figure or diagram that indicates forces (as arrows), centers of rotation, etc. Diagrams should be well-annotated.
• Experiments to test hypotheses (1-2 paragraphs)
  • You may wish to suggest some simple experiments that support your ideas about how something work (for example, I tried unscrewing a screw using both a narrow-handled and fat-handled screwdriver. For stuck screws the fat-handled screwdriver worked better. This is because, in applying the same force at the outside of the handle, I apply a greater torque on the shaft to turn the screw, as the force is applied further away from the axis of rotation (the shaft). Describe them and the results to conclude your report.

Your report should have these above sections and figures. The figure (can be hand-drawn) should include appropriate forces, velocities, torques, etc., drawn (as arrows) and labeled.

NOTE: LIST Books or URLS (web addresses) that were USED TO WRITE YOUR REPORTS.

The following can be done for extra credit:

• Experiment Proposal Outline (optional, for extra credit) to test hypotheses (1-2 paragraphs, on separate sheet!)
  • Propose a simple experiment that tests your explanation for how something (tool, sport, etc.) works. This separate sheet should include:
    • Drawing of experiment, with everything labeled.
    • Statement of what is to be tested (e.g., narrow- vs. fat-handled screwdrivers for ease of driving screws... should see a change in torque exerted on a screw given a constant applied force (lever arm, r, is changing), according to: torque = lever arm x force.
    • Prediction of outcome (it will be easier to put screw in when screwdriver handle is fatter)

Turn in your Experiment Proposal Outline to Dr. Livelybrooks (regular turn-in box) on a separate sheet, along with your report (above)

Experiment Report (optional, for extra credit) (3-4 paragraphs, on separate sheet!, due Weds, 2-June by 5pm)

• • Give table or graph indicating outcome of your experiment(s).
  • Include drawing of experiment, with everything labeled (can be recycled from your experiment outline).
  • Discuss whether the outcome matched your predictions. If it did, explain why you interpret it that way. If it didn't, explain how your predictions were wrong.
  • Summary-- summarize your experiment.

Turn in your Experiment Report to Dr. Livelybrooks (regular turn-in box) by Wednesday, 2-June (5pm).

Experiment Presentation (optional, for extra credit) (on overheads, to be presented in lab section Thursday or Friday, 3/4-June.)

• • Give overhead of idea to be tested (from Proposal). Include physics principles and variables.
  • Include drawing of experiment on overhead, with everything labeled (can be recycled from your experiment outline).
  • Give overhead with prediction of experiment outcome
  • Give overhead with data on overhead, either as a table, graph or in (brief!) observations.
  • Give overhead with explanation of whether prediction was correct or incorrect.
  • Give summary overhead.

Report ideas (here are just a few):

• Bicycles-- gears, wheels, how to turn corners, how brakes work.
• Ice skating-- how skates slide across ice, how propulsion is achieved, that spin thing with the arms.
• Tools-- how hammers work, how a "cheater bar" works with a wrench, how a zipper works, using a "come-along."
• Sports-- how to throw a curve ball, how bats propel balls, the high jump, how a kick propels a soccer (ahem, football!) ball, why does a hammer thrower spin?, bouncing a basketball.

Review

Why would the egg laid by a cliff bird be so pointy?

Why does a drag racer look so funny?

Not them the car!

It is built extremely long in order to get the largest rotational inertia with the least mass. You can see why this is important below. Later we will discuss what causes the wheelie problem in the first place. You can also understand why the front wheels are so wimpy looking by considering their own rotational inertia.

Torques

Why is it harder to hold something at shoulder height with your arm straight than with it bent? The weight of the object certainly doesn’t depend on how close it is to your body.

That is true, but the torque does.

Torque is the rotational motion counterpart of force.

Just like a net force will change an object’s linear motion, applying a net torque will change an object’s rotational motion.

Torque is different from force in the same way that rotational inertia is different from linear inertia. Torque and rotational inertia both depend on the distance to the axis of rotation. For torque the distance between the axis of rotation and an applied force is called the lever arm.

Torque = lever arm x force

When the net torque acting on something is zero there will be no change in its rotational motion. This is the rotational motion equivalent to Newton's first law.

Two children can balance a seesaw when the weight of each produces an equal torque about the pivot in opposite directions (clockwise and counter clockwise). They can do this even when they have very different weights since they can adjust each lever arm (where they sit related to the pivot) to compensate for the difference in the forces they exert. How about a kid with no friends? He can still use a seesaw! (there's hope for the lonely...)

Torque and Simple Machines

You might get a bright idea from thinking about kids on a seesaw. If a small child can balance a large child by moving farther from the pivot point (fulcrum) then you could lift the large child using a very small force if you pushed down on the seesaw far enough away from the fulcrum. Congratulations! You just invented a machine called the lever! A machine is a devise that multiplies a force and/or changes the direction of the force.

Oops, your ambitious buddy overheard you discussing your invention and has just run off to patent the lever as a way to amplify energy. He saw how easily you lifted the large child and reasons that surely the lever allowed you to increase the Potential Energy of the child by more than the amount of work you did. Are you worried that your so-called friend will make millions off your invention in this way and leave you out in the cold?

Think of all the deep questions that you can answer now that you know about Torque.

• Why is it easier to hold something over your head rather than out to your side?
• Why is it easier to walk carrying two heavy suitcases rather than just one?
• Why was the steering wheel so large on older buses and trucks? (hint: before power steering.)
• Why are doorknobs always at the edge of the door opposite from the hinges?
• Why does changing gears on my bike change how much force I need to put on the pedals? (This takes some thought.)
• Oh yes, why does a dragster tend to do a wheelie?

The torque about the axle can cause either of two rotations. Either the wheels rotate about the axle or else the car rotates about the axle.

Most people prefer to have the wheels rotate, but as the torque is increased in order to get a huge acceleration at the start that can be a challenge. Although the wheels have much less rotational inertia than the car they are still very hard to accelerate because rolling forward is resisted by the linear inertia of the entire car.

Centripital Force – “And now for something completely different!”

Let’s think back to our discussions of inertia. We said that an object will travel forever at the same velocity (same speed in a straight line) unless a net force acts on the object. What does this tell us about an object that is moving in a circle?

An object moving in a circle is always accelerating (changing velocity but not speed) and therefore always has a net force acting on it. This force must be directed towards the center of the circle. Any force that is directed towards a fixed center is a Centripetal ("center-seeking") Force.

If I whirl a bucket on the end of a string I am constantly pulling towards the center, supplying a centripetal force, in order to cause the bucket to move in a circular path.

Remember your buddy who we shrunk and wasn’t so smart? Well you decided not to re-enlarge him after all and now he’s going for a ride in the bucket. Your buddy is terrified that he will fall out while the bucket is upside-down. He keeps screaming that he wants you to slow down. Do you think that would really be in his best interest?

Once you finally let your buddy out of the bucket (and reluctantly re-enlarge him after letting his temper cool down) you ask him what it was like in the bucket. He describes feeling very heavy during the times when you spun the bucket fast and lighter when you slowed it down.

His conclusion is that a centrifugal force was pulling him towards the bottom of the bucket. You, however, remember from your physics class that there really is no centrifugal force. The combination of his inertia and the bucket pushing him into a circular path create a situation that is almost indistinguishable from gravity for your buddy in the bucket.

For another take on centrifugal forces, think of riding in a car when the car suddenly lurches left to avoid a pedestrian. During this process your upper body and head feel as if they are pushed to the right. In reality, they lack the centripital (center-seeking) force needed to make them move left with the car. Their inertia before the car veers has them going in a straight line. Thus, you seem to feel a centrifugal (outwards) force when the car veers. This is the basis for artificial gravity.

Weigh the Earth

Good old Earth seems a bit pudgy these days, what with global warming and melting ice shelves and all. Let's see if its been gaining weight.

How can we do this? Hook it up the a spring scale?

How about we use Newton's Universal Law of Gravity (it slices, it dices...)?

Weightlessness

Those astronauts floating around in the space shuttle. They're just too far from Earth to be significantly affected by its gravity, right? NOT!

Say that astronauts are orbiting the Earth at about 200 miles (320,000 meters) above the surface. The Earth's radius is 6,370,000m, so the astronauts are 6,690,000 meters above the center of the Earth.

The increase in distance from the Earth's center is:

6,690,000/6,370,000 = 1.05

or about 5%. Does this result in a significant decrease in "g" in space? (remember, "g" is the acceleration due to gravity at the Earth's surface.)

What about when we drop or accelerate upwards in an elevator?

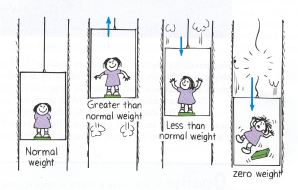
What does Newton's Law have to say about these situations?

Gravitational Fields

We represent "action at a distance" forces like gravity, electricity and magnetism using the notion of the "field."

Definition: A field arrow gives the direction of the force. Either the length of the arrow or the density of arrows represents the field's "strength" (force it can impart on a given unit).

How do we draw gravity field arrows for the Earth?

Projectile Motion

We call this motion (ball rolling of the end of table) projectile motion. It describes the motion of baseballs, cannonballs, divers at the pool, etc.

What do we notice about our projectile motion experiment?

• Both balls hit at the same time.
• One can time the drop of the one ball to determine how long the other ball moves horizontally.
• It is useful to know the time of flight of the other ball. If one knows its horizontal velocity, one can say how far (horizontally) it travels.

This information can be used to launch satellites!

In launching satellites, we seek to match the curvature of the Earth.

Satellites are groovy! (or bulgy?)

Many orbits are "elliptical" instead of circles. What does that mean?

Work-Energy Relationship for Satellites

What is the energy situation of a satellite in orbit?

Circular orbit:

• Does its kinetic energy (KE) change as it orbits? Why or why not?
• Does its gravitational potential energy (GPE) change as it orbits? Why or why not?
• What about its total energy?

Elliptical orbit:

Does its kinetic energy (KE) change as it orbits? Why or why not?

Does its gravitational potential energy (GPE) change as it orbits? Why or why not?

What about its total energy?

What does the force look like on a satellite in an elliptical orbit?

Previous Lecture Next Lecture Back to Course Page.