The amount of energy emitted from stars is determined by measuring their
brightness or the amount of light they emit. This is called photometry.
However, two major developments expanded our understanding of the
chemical make-up of stars. They were:
And the discovery that elements emit a unique spectrum, i.e.
produce a unique chemical fingerprint in the spectrum.
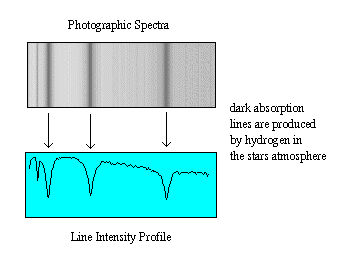The two discoveries combined to produce a new field called spectroscopy,
and allowed astronomers to measure the chemical composition of
stars for the first time.
Three leaders in this field were:
Fraunhofer who, in the early
1800's, magnified the Sun's spectrum and discovers spectral lines
Kirchhoff who, in the mid-1800's,
developed the three laws of spectroscopic analysis
which, in turn, is used to determine the chemical composition of the Sun
and stars.
Lockyer who, in the late-1800's,
discovered an unknown element in the Sun, later named helium.
Kirchhoff's Laws:
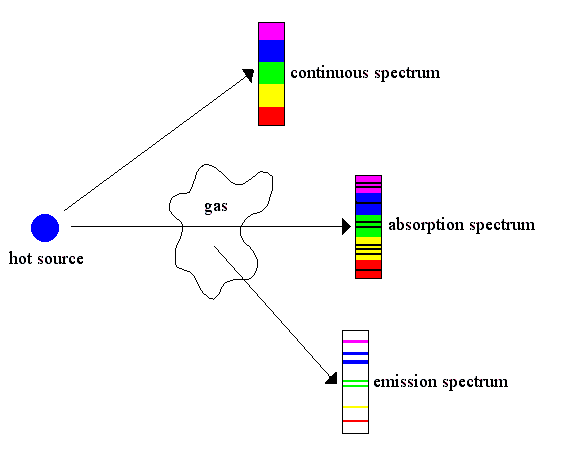
Kirchhoff showed that there are three types of spectra emitted by objects:
1) Continuous spectrum - a solid or liquid body radiates an uninterrupted,
smooth spectrum (called a Planck
curve)
2) Emission spectrum - a radiating gas produces a spectrum of discrete spectral
lines
3) Absorption spectrum - a continuous spectrum that passes through a cool gas
has specific spectral lines removed (inverse of an emission spectrum)
Planck's curve:
One of the primary results from the field of spectroscopy was the
discovery of how the spectrum of an object changes with temperature. In
particular, was the formulation of the two laws of radiation:
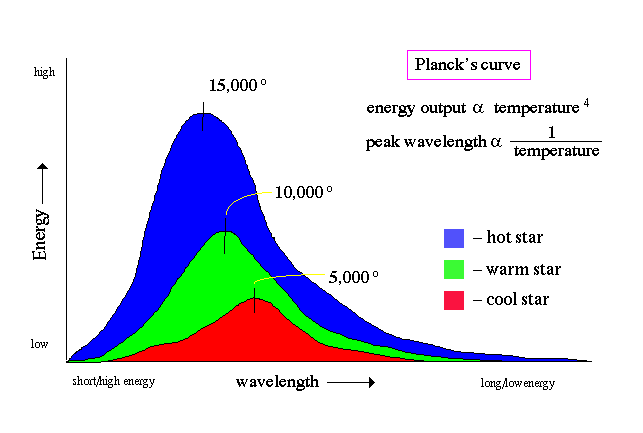
Wien's law: the peak of emission moves to bluer light as
temperature increases
Stellar Types and Planck Curve
Stefan-Boltzmann's law relates the energy output of a luminous object, in ergs, with its temperature, in Kelvins
(note that Kelvin is a measure of temperature from absolute zero), such that:
E = σ T4
where σ is Stefan-Boltzmann's constant of 5.67x10-5 erg cm-2 sec-1
Kelvins-4.
Again, it is often easier to talk in terms of ratios for two objects of temperatures, T1 and
T2, and their energy output is E1 and E2 such that:
E1/E2 =
(σT14)/(σT24)
notice that the σ's cancel out and we have
E1/E2 =
T14/T24
Wien's law determines the peak wavelength emitted by an object, and is given by:
λ = 0.29/T
So, for example, the Sun, which has a surface temperature of 5500K, emits its peak energy at
λSun = 0.29/5500 = 5.5x10-5 cm
where yellow light is about 5.2x10-5 cm.
Wave-Particle Dualism:
The wave-like nature of light explains most of its properties:
- reflection/refraction
- diffraction/interference
- energy transport
- Doppler effect
But, the results from spectroscopy (emission and absorption spectra)
can only be explained if light has a particle nature as shown by Bohr's atom
and the photon description of light.
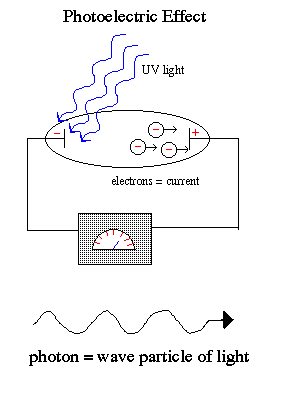
This dualism to the nature of light is best demonstrated by the photoelectric effect, where
a weak UV light produces a current flow (releases electrons) but a strong red
light does not release electrons no matter how intense the red light.
Einstein explained that
light exists in a particle-like state as packets of energy (quanta)
called photons. The photoelectric effect occurs because the packets of
energy carried by each individual red photons are too weak to knock
the electrons off the atoms no matter how many red photons you beamed onto the
cathode. But the individual UV photons were each strong enough to release the
electron and cause a current flow.
It is one of the strange, but fundamental, concepts in modern physics that
light has both a wave and particle state (but not at the same time).
Quantum Physics :
The word quantum derives from
quantity and refers to a small packet of action or process, the smallest unit
of either that can be associated with a single event in the microscopic
world.
Changes in energy, such as the transition of an electron from one orbit
to another, are done in discrete quanta. Quanta are not divisible. The
term `quantum leap' refers to the abrupt movement from one discrete energy
level to another, with no smooth transition. There is no
`inbetween'.
The quantization, or `jumpiness' of action, as depicted in quantum physics,
differs sharply from classical physics which represented motion as smooth,
continuous change.
The field of quantum
mechanics concerns the description of phenomenon on small scales where
classical physics breaks down.
The quantum world can be not be perceived directly, but rather through
the use of instruments. The question of the reality of quantum
properties remains unsolved. All quantum mechanical principles must
reduce to Newtonian principles at the macroscopic level (there is a
continuity between quantum and Newtonian mechanics).
Emission and Absorption of Light with the Bohr atom:
Bohr developed a different
model of the atom to account for quantum physics, and
the spectra of elements. The Bohr atom is similar to Rutherford
atom, except the electrons moved in fixed or quantized orbits.
The quantized orbits of the electrons allows for a simple explanation
of the origin of photons, and the spectrum of light. Photons are
produced by the transition of electrons downward in their orbits. A
downward transition releases potential energy in the form of a light
particle, a photon. Likewise, photons could be absorbed by
electrons, and they move upward in their orbits.
The Bohr atom was successful in explaining the `fingerprint' nature to
spectra, and later advances in quantum physics lead to an understand of
many of the processes of the atom.
