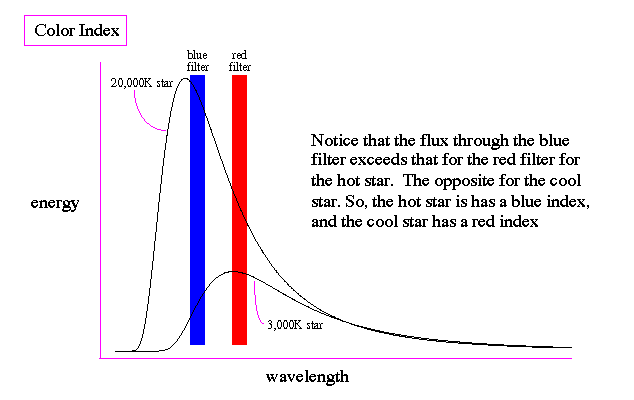
|
Stellar Color:
| Readings: Schneider & Arny: Units 55, 57 |
| (Audio Lecture) |
Stars have a range of colors which represent their surface temperatures due to Wien's law (which states that the peak emission of light from an object goes as the inverse of temperature). The color of a star is determined by that part of the visible spectrum where the peak amount of radiation is emitted.
Blue stars are extremely hot, red stars are relatively cool. Temperature here is a relative thing; cool means temperatures near 2,000 to 3,000K, about 15 times hotter than your oven. Blue stars have temperatures near 20,000K. The Sun is an intermediate yellow star with a surface temperature of 6,000K. The color of a star is determined by measuring its color index.

It is important to remember temperature and luminosity for a star are not strictly related. Stefan-Boltzmann's law states that the amount of energy emitted goes as the temperature to the 4th power; but, this relation is only strictly true for an object that is a point source (i.e. it has no size). The temperature of a normal object is proportional to its surface area (for example, things cool faster if you spread them out = increase their surface area).

So, it is possible for a star to be very bright (emit alot of energy) yet, be cool and red. We will see below that this means the star must be very large to be both bright and cool.
Stellar Spectral Type:
Stars are divided into a series of spectral types based on the appearance of their absorption spectra. Some stars have a strong signature of hydrogen (O and B stars), others have weak hydrogen lines, but strong lines of calcium and magnesium (G and K stars). After years of cataloging stars, they were divided into 7 basic classes: O, B, A, F, G, K and M. Note that the spectra classes are also divisions of temperature such that O stars are hot, M stars are cool.
Between the classes there were 10 subdivisions numbered 0 to 9. For example, our Sun is a G2 star. Sirius, a hot blue star, is type B3.
Why do some stars have strong lines of hydrogen, others strong lines of calcium? The answer was not composition (all stars are 95% hydrogen) but rather surface temperature.
As temperature increases, electrons are kicked up to higher levels (remember the Bohr model) by collisions with other atoms. Large atoms have more kinetic energy, and their electrons are excited first, followed by lower mass atoms.
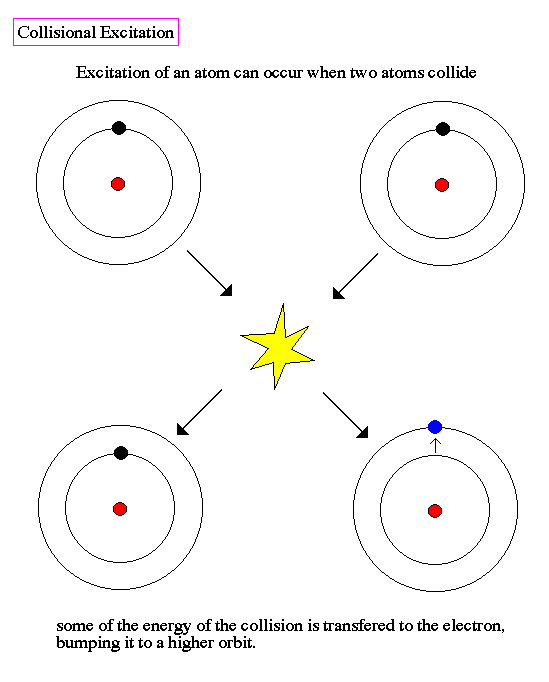
If the collision is strong enough (high temperatures) then the electron is knocked off the atom and we say the atom is ionized. So as we go from low temperatures in stars (couple 1,000K) we see heavy atoms, like calcium and magnesium, in the stars spectrum. As the temperature increases, we see lighter atoms, such as hydrogen (the heavier atoms are all ionized by this point and have no electrons to produce absorption lines).
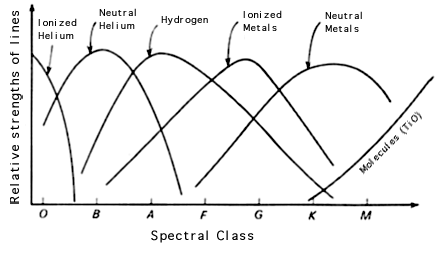
As we will see later, hotter stars are also more massive stars (more energy burned in the core). So the spectral classes of stars is actually a range of masses, temperatures, sizes and luminosity. For normal stars (called main sequence stars) the following table gives their properties:
type Mass Temp Radius Lum (Sun=1) ------------------------------------------- O 60.0 50,000 15.0 1,400,000 B 18.0 28,000 7.0 20,000 A 3.2 10,000 2.5 80 F 1.7 7,400 1.3 6 G 1.1 6,000 1.1 1.2 K 0.8 4,900 0.9 0.4 M 0.3 3,000 0.4 0.04 -------------------------------------------

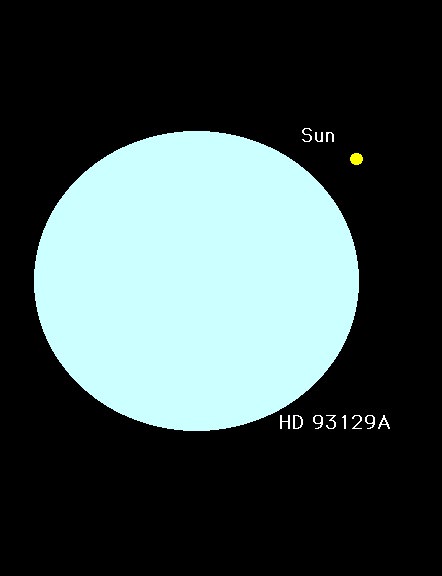
A B star is much larger, brighter and hotter. An example is HD93129A shown below:
Luminosity Classes:
Closer examination of the spectra of stars shows that there are small changes in the patterns of the atoms that indicate that stars can be separated by size called luminosity classes.
The strength of a spectra line is determined by what percentage of that element is ionized. An atom that is ionized has had all its electrons stripped off and can not absorb photons. At low densities, collisions between atoms are rare and they are not ionized. At higher densities, more and more of the atoms of a particular element become ionized, and the spectral lines become weak.
One way to increase density at the surface of a star is by increasing surface gravity. The strength of gravity at the surface of a star is determined by its mass and its radius (remember escape velocity). For two stars of the same mass, but different sizes, the larger star has a lower surface gravity = lower density = less ionization = sharper spectral lines (the opposite is true, higher gravity = higher density = broader spectral lines, this is called pressure broadening).
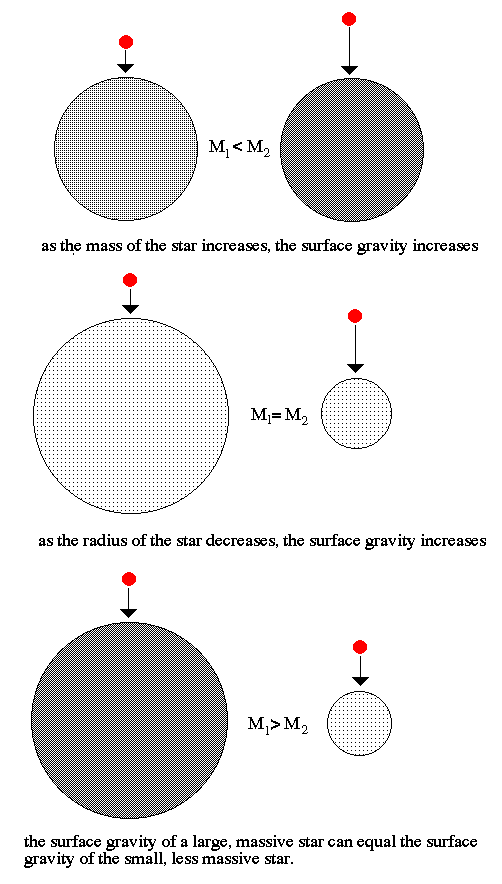
This was applied to all stars and it was found that stars divide into five luminosity classes: I, II, III, IV and V. Stars of type I and II are called supergiants, being very large (low surface gravity), stars of type III and IV are called giant stars. Stars of type V are called dwarfs. The Sun is a G2 V type stars.
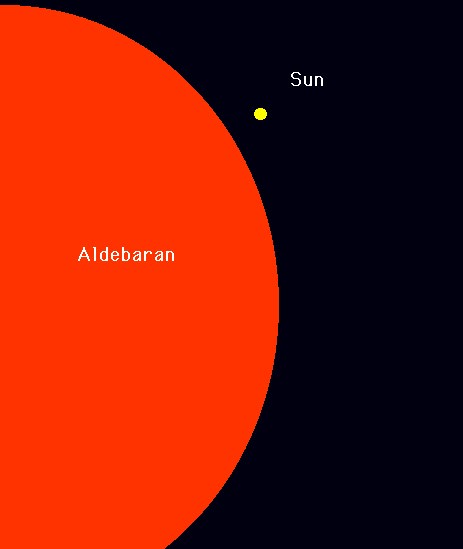
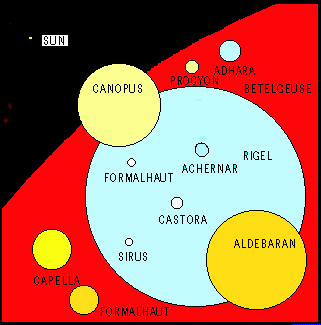
So now we have a range of stellar colors and sizes. For example, Aldebaran is a red supergiant star:
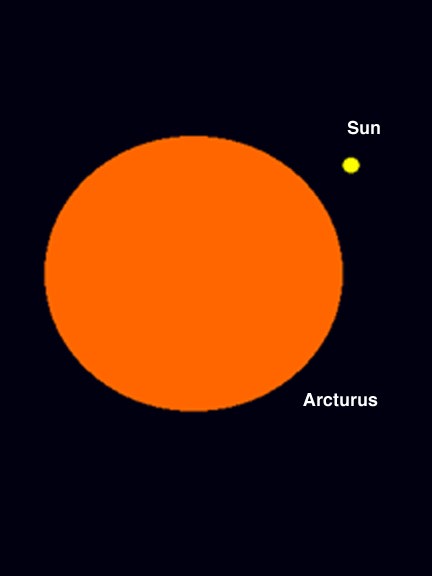
Arcturus is an orange giant star:
HST imaging found that Betelgeuse is one of the largest stars, almost the size of our whole solar system.

The other extreme was also found, that there exist a class of very small stars called white and brown dwarfs, with sizes close to the size of the Earth:

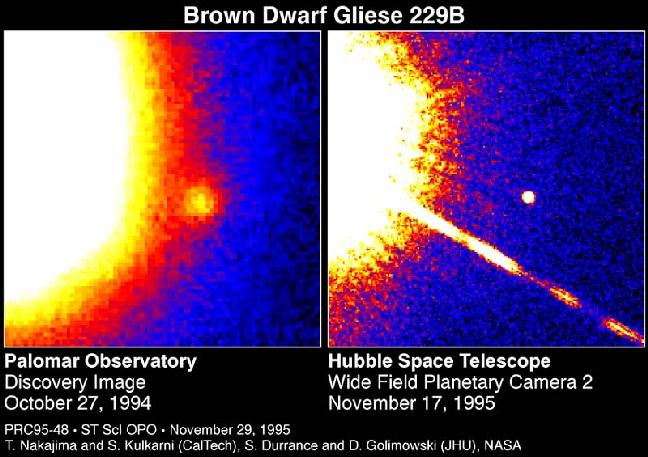
Red and blue supergiant stars, as well as giant stars exist. The following is a comparison of these types.
Luminosity Function:
Surveying the skies for stars is a very biased method of doing science since clearly the brightest stars are the easiest to observe. But are the brightest stars typical of the stellar population? To determine what a typical star is like we construct a luminosity function, the number of stars as a function of absolute magnitude in the form of a histogram.
A luminosity function is constructed by sampling a volume of space and counting all the stars in that volume. The resulting plot will look like the diagram below:
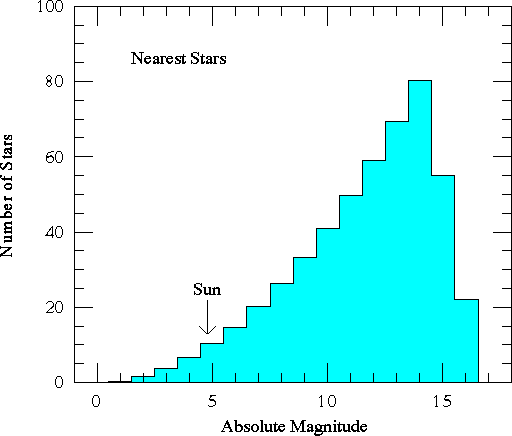
Notice that the most common type of star is actually small, low luminosity stars. Bright stars are quite rare (although they can be seen from great distances). Since luminosity is correlated with mass, then this means that high mass stars are rare.
Russell-Vogt Theorem:
Despite the range of stellar luminosities, temperatures and luminosities, there is one unifying physical parameter. And that is the mass of the star. Hot, bright stars are typically high in mass. Faint, cool stars are typically low in mass. This sole dependence on mass is so strong that it is given a special name, the Russell-Vogt Theorem.
The Russell-Vogt Theorem states that all the parameters of a star (its spectral type, luminosity, size, radius and temperature) are determined primarily by its mass. The emphasis on `primarily' is important since we will soon see that this only applies during the `normal' or hydrogen burning phase of a star's life. A star can evolve, and change its size and temperature. But, for most of the lifetime of a star, the Russell-Vogt Theorem is correct, mass determines everything.

|
|

|