Readings: Rationalism
Geocentric Cosmology
Ptolemy

Rationalism:

Science, it is widely agreed, originated from two main sources. One was the need to develop practical knowledge and to pass it from generation to generation. The other was a more spiritual concern with the nature and origin of the world. Common to both of these well-springs of science was an appreciation of the regularity of Nature. One of the first scientists to make frequent use of the concept of a law of Nature, in the sense that we now use that term, was the Franciscan friar and scholar Roger Bacon (c. 1214-1292).

He helped to prepare the way for those who, irrespective of their own religious beliefs, insisted that the scientific investigation of Nature should be rooted in experiment and conducted on a purely rational basis, without reference to dogmatic authority. Laws of Nature are now a central part of science. Carefully defined concepts, often expressed in mathematical terms, are related by natural laws which are themselves often expressed in a mathematical form.

The earliest beginnings of science was to note that there exist patterns of cause and effect that are manifestations of the Universe's rational order. We mostly develop this idea as small children (touch hot stove = burn/pain). But the extrapolation of a rational order to cosmology requires a leap of faith in the beginning years of science, later supported by observation and experimentation.

Thus, the main purpose of science is to trace, within the chaos and flux of phenomena, a consistent structure with order and meaning. This is called the philosophy of rationalism. The purpose of scientific understanding is to coordinate our experiences and bring them into a logical system.

Thoughout history, intellectual efforts are directed towards the discovery of pattern, system and structure, with a special emphasis on order. Why? control of the unpredictable, fear of the unknown, and a person who seeks to understand and discover is called a scientist.

Science is founded on the hope that the world is rational in all its observable aspects. Its possible that there may be some facets of reality which lie beyond the power of human reasoning, that there may be things with explanations that we could never grasp, or no explanation at all, but the fact that the world is rational is connected with the fact that it is ordered.

Eratosthenes:

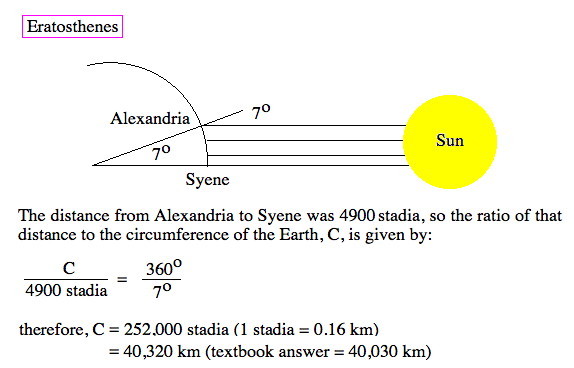
Between the cosmological foundation set by the Presocratics and the world of Ideas introduced by Plato was a set of fundamental calculations on the size of the Earth, Moon, Sun and the distances between the nearby planets performed by Eratosthenes and Aristarchus (c. 250 BC). Using some simple geometry, these two natural philosophers were able to, for the first time, place some estimate of the size of the cosmos in Earth terms.

For a long time it was realized that the earth's surface was curved by people familiar with the behavior of incoming and outgoing ships. For it was obvious that as a ship passed over the horizon, the hull disappeared first, then the topmost sailing masts (although one could argue this is an effect of refraction in the atmosphere). Ancient astronomers could see with their eyes that the Sun and the Moon were round. And the shadow of the Earth, cast on the lunar surface during a lunar eclipse, is curved. A sphere is the simplest shape to explain the Earth's shadow (a disk would sometimes display a shadow shaped like a line or oval).

Eratosthenes used a spherical Earth model, and some simple geometry, to calculate its circumference. Eratosthenes knows that on a special day (the summer solstice) at noon in the Egyptian city of Syene, a stick placed in the ground will cast no shadow (i.e., it is parallel to the Sun's rays). A stick in the ground at Alexandria, to the north, will cast a shadow at an angle of 7 degrees. Eratosthenes realizes that the ratio of a complete circle (360 degrees) to 7 degrees is the same as the ratio of the circumference of the Earth to the distance from Alexandria to Swenet. Centuries of surveying by Egyptian pharaohs scribes gave him the distance between the two cities of 4900 stadia, approximately 784 kilometers. This resulting in a circumference of 40,320 kilometers, which is amazingly close to the modern value of 40,030 kilometers. With this calculation, Eratosthenes becomes the father of geography eventually drawing up the first maps of the known world and determining the size of the most fundamental object in the Universe, our own planet.

Geometric Cosmology:

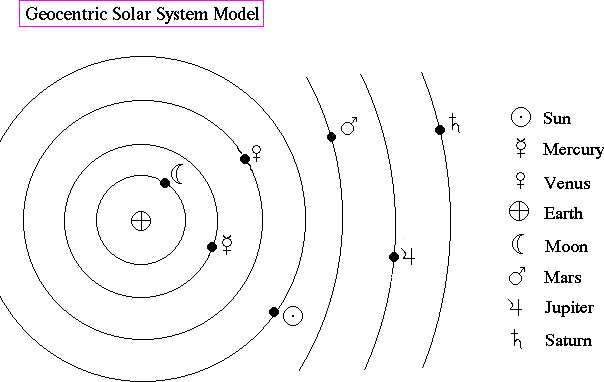
There were only seven objects visible to the ancients, the Sun and the Moon, plus the five planets, Mercury, Venus, Mars, Jupiter and Saturn. It was obvious that the planets were not on the celestial sphere since the Moon clearly passes in front of the Sun and planets, plus Mercury and Venus can be seen to transit the Sun. Plato first proposed that the planets followed perfect circular orbits around the Earth. Later, Heraclides (330 B.C.) developed the first Solar System model, placing the planets in order from the Earth it was is now called the geocentric solar system model.

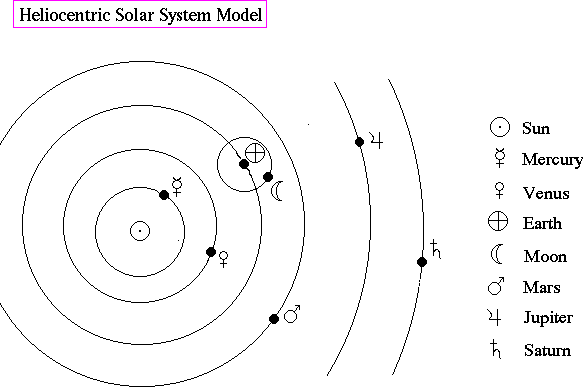
Note that orbits are perfect circles (for philosophical reasons = all things in the Heavens are "perfect"). Heraclides model became our first cosmology of things outside the Earth's atmosphere.

Slightly later, Aristarchus (270 B.C.) proposed an alternative model of the Solar System placing the Sun at the center with the Earth and the planets in circular orbit around it. The Moon orbits around the Earth. This model became known as the heliocentric theory

Aristarchus was the first to propose a Sun centered cosmology and one of the primary objections to the heliocentric model is that the stars display no parallax (the apparent shift of nearby stars on the sky due to the Earth's motion around the Sun). However, Aristarchus believed that the stars were very distant and, thus, display parallax's that are too small to be seen with the eye (in fact, the first parallax will not by measured until 1838 by Friedrich Bessel). The Sun is like the fixed stars, states Aristarchus, unmoving on a sphere with the Sun at its center. For Aristarchus it was absurd that the "Hearth" of the sky, the Sun, should move and eclipses are easy to explain by the motion of the Moon around the Earth.

Problems for Heliocentric Theory:

While today we know that the Sun is at the center of the solar system, this was not obvious for the technology of the times per-1500's. In particular, Aristarchus' model was ruled out by the philosophers at the time for three reasons:

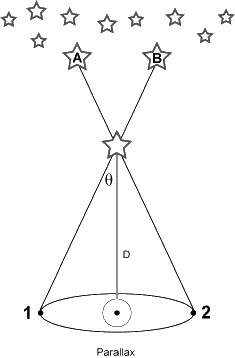
  1. Earth in orbit around Sun means that the Earth is in motion. Before the discovery of Newton's law of motion, it was impossible to imagine motion without being able to `feel' it. Clearly, no motion is detected (although trade winds are due to the Earth's rotation).
  2. If the Earth undergoes a circular orbit, then nearby stars would have a parallax. A parallax is an apparent shift in the position of nearby stars relative to distant stars.

    Of course, if all the stars are implanted on the crystal celestial sphere, then there is no parallax.

  3. Lastly, geocentric ideas seem more `natural' to a philosopher. Earth at the center of the Universe is a very ego-centric idea, and has an aesthetic appeal.

Ptolemy:

Ptolemy (200 A.D.) was an ancient astronomer, geographer, and mathematician who took the geocentric theory of the solar system and gave it a mathematical foundation (called the "Ptolemaic system"). He did this in order to simultaneously produce a cosmological theory based on Aristotle's physics (circular motion, no voids, geocentric) and one that would provide a technically accurate description of planetary astronomy. Ptolemy's system is one of the first examples of scientists attempting to "save the phenomena", to develop a combination of perfect circles to match the irregular motion of the planets, i.e., using concepts asserted by pure reason that match the observed phenomenon.

Ptolemy wrote a great treatise on the celestial sphere and the motion of the planets call the Almagest. The Almagest is divided into 13 books, each of which deals with certain astronomical concepts pertaining to stars and to objects in the solar system. It was, no doubt, the encyclopedic nature of the work that made the Almagest so useful to later astronomers and that gave the views contained in it so profound an influence. In essence, it is a synthesis of the results obtained by Greek astronomy; it is also the major source of knowledge about the work of Hipparchus.

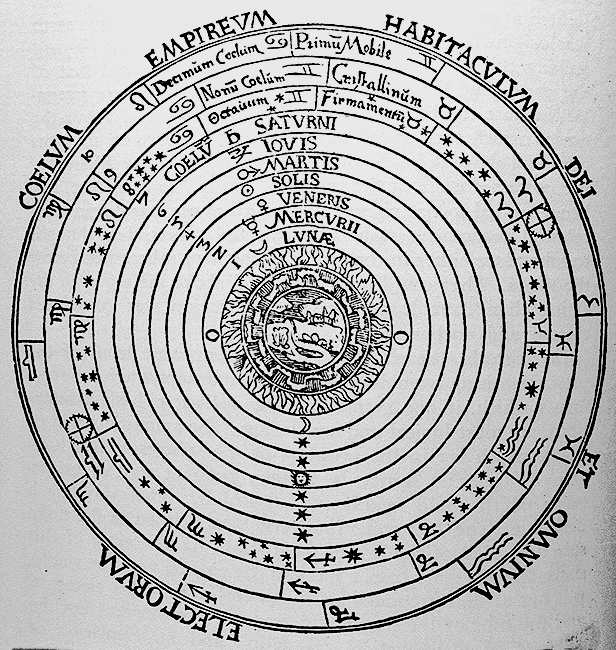
The Christian Aristotelian cosmos, engraving from Peter Apian's Cosmographia, 1524

In the first book of the Almagest, Ptolemy describes his geocentric system and gives various arguments to prove that, in its position at the center of the universe, the Earth must be immovable. Not least, he showed that if the Earth moved, as some earlier philosophers had suggested, then certain phenomena should in consequence be observed. In particular, Ptolemy argued that since all bodies fall to the center of the universe, the Earth must be fixed there at the center, otherwise falling objects would not be seen to drop toward the center of the Earth. Again, if the Earth rotated once every 24 hours, a body thrown vertically upward should not fall back to the same place, as it was seen to do. Ptolemy was able to demonstrate, however, that no contrary observations had ever been obtained.

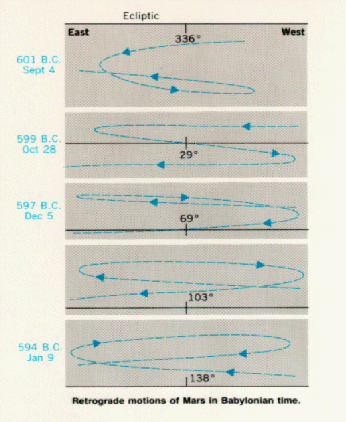
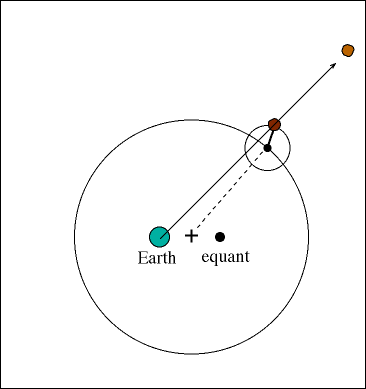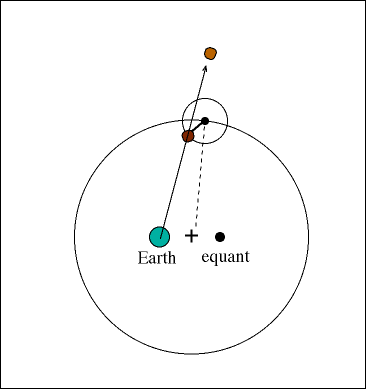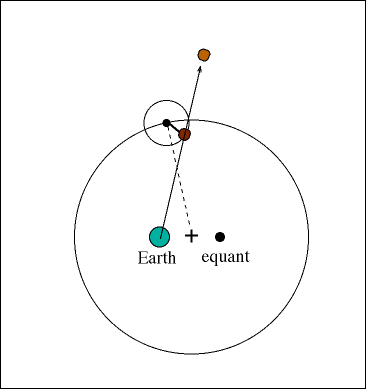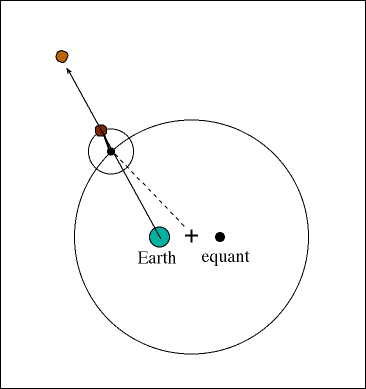
Ptolemy accepted the following order for celestial objects in the solar system: Earth (center), Moon, Mercury, Venus, Sun, Mars, Jupiter, and Saturn. However, when the detailed observations of the planets in the skies is examined, the planets undergo motion which is impossible to explain in the geocentric model, a backward track for the outer planets. This behavior is called retrograde motion.


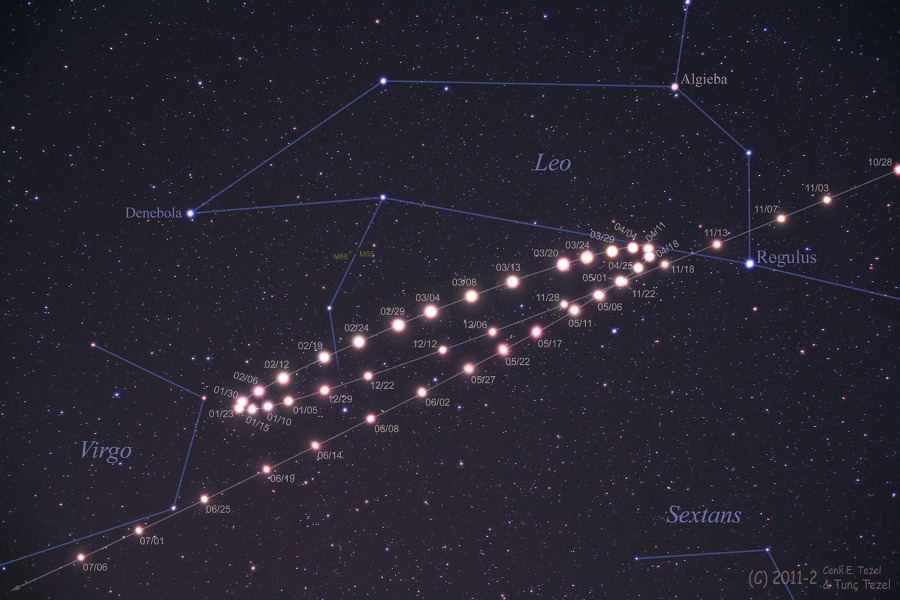
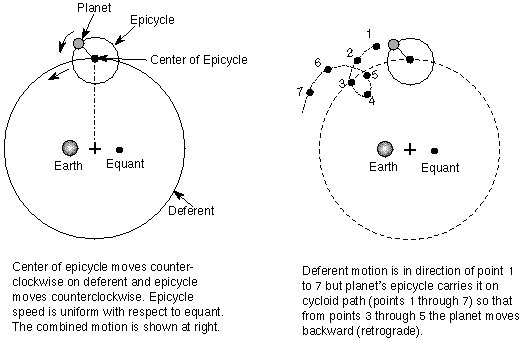
Retrograde motion for Mars, notice how Mars increases in brightness in the middle of the cycle (due to Earth's closest approach)

He realized, as had Hipparchus, that the inequalities in the motions of these heavenly bodies necessitated either a system of deferents and epicycles or one of movable eccentrics (both systems devised by Apollonius of Perga, the Greek geometer of the 3rd century BC) in order to account for their movements in terms of uniform circular motion.

In the Ptolemaic system, deferents were large circles centered on the Earth, and epicycles were small circles whose centers moved around the circumferences of the deferents. The Sun, Moon, and planets moved around the circumference of their own epicycles. In the movable eccentric, there was one circle; this was centered on a point displaced from the Earth, with the planet moving around the circumference. These were mathematically equivalent schemes.

Even with these, all observed planetary phenomena still could not be fully taken into account. Ptolemy therefore exhibited brilliant ingenuity by introducing still another concept. He supposed that the Earth was located a short distance from the center of the deferent for each planet and that the center of the planet's deferent and the epicycle described uniform circular motion around what he called the equant, which was an imaginary point that he placed on the diameter of the deferent but at a position opposite to that of the Earth from the center of the deferent (i.e., the center of the deferent was between the Earth and the equant). He further supposed that the distance from the Earth to the center of the deferent was equal to the distance from the center of the deferent to the equant. With this hypothesis, Ptolemy could better account for many observed planetary phenomena.

Although Ptolemy realized that the planets were much closer to the Earth than the "fixed" stars, he seems to have believed in the physical existence of crystalline spheres, to which the heavenly bodies were said to be attached. Outside the sphere of the fixed stars, Ptolemy proposed other spheres, ending with the primum mobile ("prime mover"), which provided the motive power for the remaining spheres that constituted his conception of the universe. His resulting solar system model looked like the following, although the planets had as many as 28 epicycles to account for all the details of their motion.

This model, while complicated, was a complete description of the Solar System that explained, and predicted, the apparent motions of all the planets. The Ptolemic system began the 1st mathematical paradigm or framework for our understanding of Nature.

Mathematics and Cosmology

At the end of the Greek era, there is no doubt that we completed our transition from mythical, supernatural explanations of cosmology to a natural, science based description. And, it is clear, that the mathematical description of the cosmos given by Ptolemy is, in the words of the mathematical Wigner, "unreasonably effective", meaning that is mathematics is a surprisingly successful to understand the natural world, beyond our expectations given the chaos that reigns in everyday phenomenon. This is the ultimate verification of the Greek philosophical tradition which asserts that nature is understandable rather than under the control of capricious deities which are to be appeased rather than understood, is one of the roots of science. Thus, the greatest gift from the Greek was the philosophy of rationalism, that the Universe is open to inspection and, ultimately, understandable.

The Greeks were also the first to recognize the deep connection between science and mathematics. Mathematics is a natural language for rational arguments and relationships expressed mathematically are capable of being placed in logically correction chains of progression as an efficient way determining their validity. As later stated by Galileo:

Philosophy is written in this grand book, the Universe which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles and other geometric figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.

It is of continuing amazement, to both scientists and philosophers alike, that the laws of Nature can be expressed in mathematical form, and that humans are capable of processing that kind of math. However, while no one doubts the importance of mathematics to science, there is a continuing debate on the origin of math's effectiveness. On one hand, we see Plato's belief that mathematical ideas exist independent of our world, or human thought (the realist or Platonism view). In fact, for Plato, the real world is this mathematical world, not the shadow, physical world we live in. Aristotle, on the other hand, believes that math is a human invention, and that the mind is where math is created (the instrumentalist or formalist view). Humans created mathematics by idealising or abstracting elements of the physical world. In fact, mankind's extraordinary math abilities may simply be the product of millions of years of evolution providing us with powerful intellectual tools as a survival asset.

A modern view of mathematics and science is provided by Bertrand Russell who states "Mathematics is the chief source of the belief in eternal and exact truth, as well as a sensible intelligible world". This is a guiding principle for most scientists and mathematics. Scientists do create methods to quantify phenomenon in physics, chemistry and biology, and these inventions are effective. However, it should be remembered is that these mathematical methods are, in many cases, incredible accurate. So as phenomenon is studied and recorded, and as patterns emerge (via the scientific method), humans will take mathematical concepts from abstracting elements and apply them to problems. But the discovery is in the connections to science, not the mathematical objects themselves.

The bottom line about the relationship of mathematics to science is basically that math works. Mathematics is very much a part of the Universe and very necessary for understanding cosmology. For we will see, in later chapters, that there are properties to the Universe can only be understood through mathematics. For example, our senses and mental models are fixed in a three dimensional world (3D), and the macroscopic Universe is the four dimensional (4D) construct called spacetime. To explore spacetime requires an extension to our senses that only mathematics provides.

The mathematics of the Greeks was geometry and arithmetic, but as we advance forward in the history of cosmology we will encounter more sophisticated mathematics. Newton will introduce calculus, the math of infinitesimals. Einstein will introduce non-Euclidean geometry. Quantum physics uses differential equations and matrix algebra. These math methods are the windows in which we see, and understand, reality. By the 21st century, we will see a heavy usage of computers and artificial simulations to probe the vast amount of information provided by new technologies. And our sense of how we do science will change as encounter new concepts which are not testable in the traditional sense of direct observation or experimentation.

However, common to all cosmological investigations from the Greeks to modern times was an appreciation of the regularity of Nature. That Nature has, within itself, mathematical patterns that could be expressed as laws of Nature (the law of gravity, the law of conversation of energy, the Ideal Gas law, etc.). The idea that physical entities obey laws is a strictly Western invention for Eastern cultures would find it absurd for inanimate objects "understanding" laws.

Middle Ages

The period between the fall of the Roman Empire and the start of Renaissance in the 14th century is known as the Dark or Middle Ages. While the Middle Ages were considered a time of scientific stagnation due to the recurring political and social upheavals of the time, their was a continued steady progress in intellectual thought in Europe and surrounding kingdoms in the Mideast and India. While the Catholic Church dominates most knowledge enterprises during this era, their influence was not as suppressive as popularly portrayed and various Church institutions were mostly responsible for the preservation of cosmological ideas from the Greeks.

The distinction between what makes up matter (the primary elements) and its form became a medieval Christian preoccupation, with the sinfulness of the material world opposed to the holiness of the heavenly realm (which is interesting since modern cosmology is heavily consumed with the issue of dark matter). The medieval Christian cosmology placed the heavens in a realm of perfection, derived from Plato's Theory of Forms

While adopting most of Aristotle's worldview into Christian thought, his finite Universe was at odds with the Church's idea of God of infinite power. If God is without limit then he can not be bounded in one place. Thus, the Church proposed an unlimited Universe rather than an infinite Universe, a subtle difference.

A heliocentric Universe was impossible for the Church to adopt. In the end, medieval cosmology centers on the balance of angelic sphere and the earthy realm. One such cosmology is found in Dante's `The Divine Comedy'.

Dante's 'Divine Comedy' is an epic poem dealing with an allegorical vision of the afterlife and Catholic world-view. Based on the Aristotelian model, the Earth in the 'Divine Comedy' is at the center of the Universe, surrounded by whirling spheres made of transparent solid matter. Added to the Aristotelian eight spheres is a ninth sphere, the primum mobile or "first moved", the source of the movement of all the inner planetary spheres. Beyond the primum mobile lies the spiritual Universe, the mind of God or Empyrean heaven, thus this sphere marks the boundary between the natural and supernatural worlds.

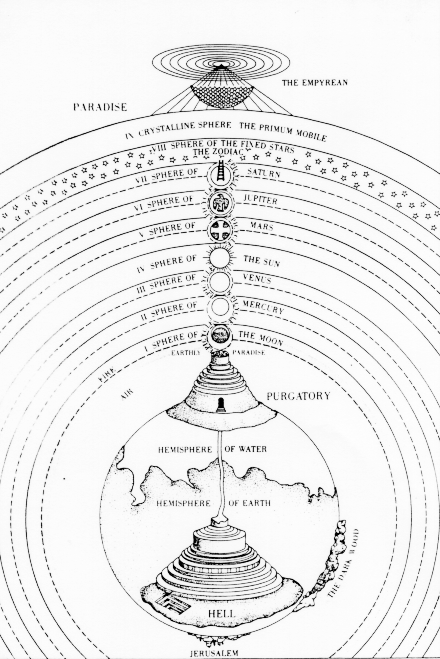
Dante's cosmology is divided into three sections, based on theological doctrine, Inferno (Hell), Purgatory and Paradise. The physical layout is such that Lucifer defines the very center of the Universe and God is found in the outer region. Inside the Earth is found Hell, divided into nine circles for increasing levels of sin. Between the surface of the Earth and sphere of the Moon lies Purgatory (a mountain divided into seven terraces, displaced from the Earth when Lucifer fall created Hell).

Above Purgatory lies the spheres of Heaven, each describing a deficiency in one of the cardinal virtues. The Moon, containing the inconstant, whose vows to God waned as the moon and thus lack fortitude; Mercury, containing the ambitious, who were virtuous for glory and thus lacked justice; and Venus, containing the lovers, whose love was directed towards another than God and thus lacked Temperance. The final four incidentally are positive examples of the cardinal virtues, all led on by the Sun, containing the prudent, whose wisdom lighted the way for the other virtues, to which the others are bound (constituting a category on its own). Mars contains the men of fortitude who died in the cause of Christianity; Jupiter contains the kings of Justice; and Saturn contains the temperant, the monks who abided to the contemplative lifestyle.

Despite the main focus on religious concepts in the 'Divine Comedy', a great deal of physical cosmology is outlined that merges religious doctrine of the time into the Ptolemaic system with scientific additions that parallel the discoveries from the time of Aristotle. For example, there are numerous references to a spherical Earth and changing constellations with latitude and varying timezones. The connection between the supernatural and the physical in Dante's cosmology mimics the Platonic viewpoint of the physical world being a copy of the world of Forms. Here the planetary spheres copy the angelic hierarchies that rotate around God (and the circles of Hell are a parody that rotates around Satan). Even the geocentric Universe is simply an imperfect copy of the spiritual form of Paradise, a theocentric Universe where the angels that power the motion of the planets are actually revolving around God, who illuminates all things from the center. With perfect symmetry in both physical and theological space, Dante's cosmology represents the peak in medieval cosmology blending the Ptolemaic system with Christian doctrine.

The political and intellectual authority of the medieval church declined with time, leading to the creative anarchy of the Renaissance. This produced a scientific and philosophical revolution including the birth of modern physics. Foremost to this new style of thinking was a strong connection between ideas and facts (the scientific method).

Since cosmology involves observations of objects very far away (therefore, very faint) advancement in our understanding of the cosmos has been very slow due to limits in our technology. This has changed dramatically in the last few years with the construction of large telescopes and the launch of space-based observatories.

Copernicus:

As we know from history, the great library at Alexandria burns in 272 AD, destroying a great deal of the astronomical data for the time. Roman culture collapses and we enter the Dark Ages. But, the Roman Catholic Church absorbs Aristotle's scientific methods and Ptolemy's model into its own doctrine. Thus, preserving the scientific method and Ptolemy's Solar System. Unfortunately, the geocentric model was accepted as doctrine and, therefore, was not subjected to the scientific method for hundreds of years.

Copernicus (1500's) reinvented the heliocentric theory and challenged Church doctrine. Copernicus (c. 1520) was not the first astronomer to challenge the geocentric model of Ptolemy, but he was the first to successfully formulate a heliocentric model and publish his model. He was able to overcome centuries of resistance to the heliocentric model for a series of political and scientific reasons. Politically, the authority of the Church was weakening in Northern Europe in the 15th century allowing more diversity in scientific thinking (although the new Protestant faiths were also not quick to embrace the heliocentric model). Scientifically, a better understanding of motion (particularly inertia) was undermining the whole concept of an unmoving Earth. A rotating Earth is a much simpler explanation for the durnal motion of stars, an Earth that rotates is only one step away from an Earth that revolves around the Sun. The heliocentric model had a greater impact than simply an improvement to solve retrograde motion. By placing the Sun at the center of the Solar System, Copernicus forced a change in our worldview = paradigm shift or science revolution.

Copernicus began his quest for an improved solar system model with some basic principles. Foremost was the postulate that the Earth was not the center of the Universe, only the center of local gravity and the Moon. Second, the postulate that the Sun was the center of the solar system, all planets revolved around the Sun. In this fashion, retrograde motion is not cause by the planets themselves, but rather by the orbit of the Earth.

While Copernicus includes a rotating Earth in his heliocentric model, he continues to cling to Aristotle's celestial motions, i.e. orbits that are perfect circles (rather than their true shape, an ellipse). This forces Copernicus to adopt a series of moving sphere's for each planet to explain longitude motion. While Copernicus has fewer sphere's, since more of the retrograde motion is accounted for, his system is still extremely complicated in a computational sense. It's two greatest advantages is that it places the inferior planets near the Sun, naturally explaining their lack of large eastern or western elongations, and removing any extreme motions, such as that needed to explain durnal changes.

Copernicus also changes the immovable empyrean heaven into a fixed sphere of stars, severing theology from cosmology. However, Copernicus fails to produce a mechanically simple scheme for astrologers to cast horoscopes or astronomers to produce almanacs, for ultimately the tables he produces are as complicated as Ptolemy's and he did not publish all his results in the final edition of his work, "On the Revolutions of the Heavenly Spheres".

However, Copernicus, like Ptolemy, also used circular orbits and had to resort to epicycles and deferents to explain retrograde motions. In fact, Copernicus was forced to use more epicycles than Ptolemy, i.e. a more complicated system of circles on circles. Thus, Copernicus' model would have failed our modern criteria that a scientific model be as simple as possible (Occam's Razor).

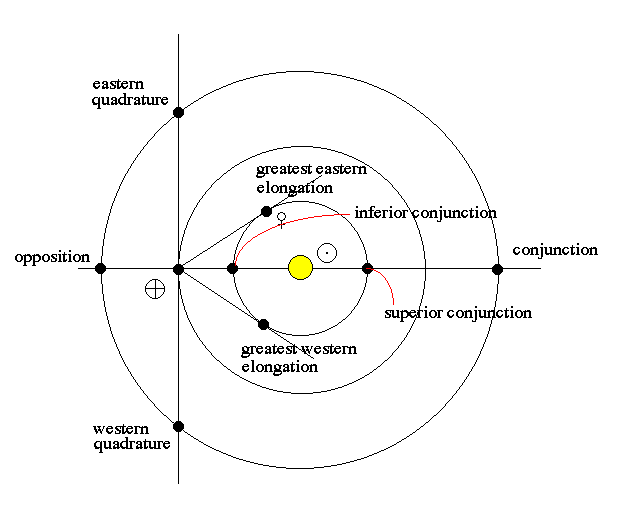
Planetary Configurations:

The planets outside of the Earth's orbit (Mars, Jupiter, Saturn, Uranus, Neptune, Pluto) are called superior planets

Likewise, the planets inside of the Earth's orbit (Mercury, Venus) are called inferior planets.

Other configurations are:

Solar System Live