Dome resonators

Mixed boundary conditions in dome cavities

Exactly solvable problems

There are only a few optical resonator geometries for which the wave equation can be solved analytically in terms of special functions. An important and well-known example is the ideal dielectric sphere, for which the solution procedure (in the context of light scattering) was found by the German physicist Gustav Mie, then at the University of Greifswald (1908). The problem is solvable because the spherical surface coincides with an iso-surface of the spherical coordinate system, and the boundary conditions are rotationally invariant as well.

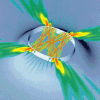
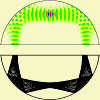
A new geometry for which at least the scalar wave equation can be solved analytically is the parabolic dome. This solution was obtained by me in collaboration with Isabelle Robert and Izo Abram (read more on a separate page: Ray and wave solutions in the parabolic dome). Here is a side view of a stationary state of the three-dimensional cavity, which has the shape of a dome:

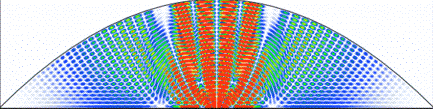
This is an exact solution of the scalar wave equation. Some fully vectorial modes in such cavities can also be written down exactly. In contrast to the Mie problem, the boundaries here are not contour surfaces of any single orthogonal coordinate system. Moreover, the cavity has mixed boundary conditions if the top mirror is a perfect electric conductor while the bottom mirror is a dielectric mirror.

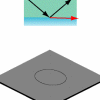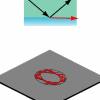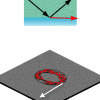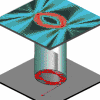
There is an extremely close connection between the exact wave solutions and the ray-optics approximation, which in this case turns out to yield quantitatively correct results for the cavity spectrum when combined with a standard semiclassical quantization approach.

Note the similarity between the above ray pattern and the wave plot above. The following link leads to additional material on this subject.

Ray and wave solutions in the parabolic dome

Taking polarization seriously

Motivated by recent progress toward fabrication of dome cavities, my graduate student David Foster and I have taken this subject one step further: we study the fully vectorial modes of dome cavities with arbitrary shapes and various, mixed boundary conditons. This includes the effects of radiation losses through realistic Bragg mirrors, and is not limited to any paraxial approximation.

Shown here is a cavity mode in two orthogonal side-view cross sections, together with its electric vector field plotted in a horizontal cross section whose location is indicated by the floating grey bars in the side views. Deviations from paraxiality then show up in the fact that the elctric field vector does not lie in a horizontal plane. The color in the vector plot indicates the magnitude of the vertical field components.

The methods used to perform these calculations, and some results, are reported in our paper: D. H. Foster and J. U. Nöckel, "Methods for 3-D vector microcavity problems involving a planar dielectric mirror", Optics Communications 234, 351-383 (2004).

Results

While applying the numerical methods to a cavity whose modes we expected to behave paraxially, an interesting polarization-dependent phenomenon showed itself: Bragg-mirror induced mixing of orbital angular momentum eigenstates in the paraxial regime. The link points to a poster presented by David Foster at CLEO/QELS in Baltimore, Maryland (May 22, 2005).
We also found that a new type of modes appears whose ray-picture anaolgues can only be understood when the Goos-Hänchen effect is taken into account. On the linked page, the physics of this effect is explained in more detail.
In addition, we developed a perturbation theory for the near-paraxial polarization mixing, in which the polarization- and angle dependent- reflectivity of the Bragg mirror controls the small parameter — see our paper "Degenerate perturbation theory describing the mixing of orbital angular momentum modes in Fabry-Pérot cavity resonators"

Last modified: Mon Oct 1 13:57:04 PDT 2012