Essentials of Physics- PHYS 101
Lecture 3
Essentials of Physics- PHYS 101
Lecture 3
average velocity is the change in position (Dp here) over the change in time, Dt.

![]() Instantaneous velocity and average velocity:
Instantaneous velocity and average velocity:
The term instantaneous velocity refers to velocity at an instant.
Average velocity is the speed averaged over the time interval, along with the direction.
![]() ...and remember, velocity is relative.
...and remember, velocity is relative.![]()
![]()
![]() Changing velocity but not speed.
Changing velocity but not speed.
Well... can we? If so, how? Can we change speed without changing velocity?
![]()
What is this thing called acceleration? We define it to be related to velocity vs. time graphs.
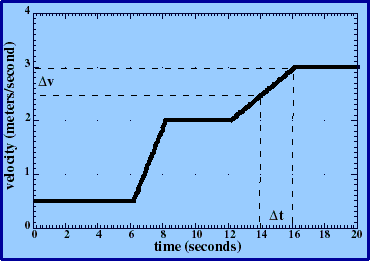
Definition: average acceleration is the change in velocity over the time elapsed.
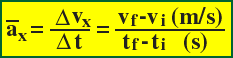
Questions:
![]()
![]()
Acceleration tells us about change in velocity. If our initial velocity is zero, then acceleration can tell us our velocity after some time using the simple relationship:
velocity acquired = acceleration x time
How Fast
Say you just ran off the end of a cliff, and plan to descend for 5 seconds before hitting the valley floor with a little puff.
In the several moments while you wait to fall (just kidding!) you estimate how fast will you will traveling when you hit:

In fact, Wile E Coyote will be travelling 10 m/s after 1 second of fall, 20 m/s after 2, 30 m/s after 3 seconds, and so on.
{note: we are ignoring the force of air resistance, which will oppose his fall and, eventually, equal the force of gravity exerted downwards on Wile (what does that tell you about the air resistance force's relationship to speed?). When this happens, Wile has reached terminal velocity and won't speed up any more (lucky guy!)}
How Far
You ran off the end of a cliff, but don't know how far you will fall. How far will you travel (ever downward!) after 5 seconds of falling?