8. Digital Representation
As described in "Sound as a Representation" there are two common ways to represent sound: as an analog representation, and as a digital representation.
An analog representation of sound uses continuous and constant voltage fluctuations that change in accordance with variations in air pressure made by sound. This representation of sound made by the voltage signal is called an analog signal. Analog signals are characterized by the fact that voltages representing the sound are constantly changing.
Digital sampling is the process of converting an analog representation of sound to a digital representation of sound. In digital sampling, numbers (as "digital" indicates) are used to represent sound.

Diagram 8-1: The analog signal may be sent to an analog to digital converter (A/D converter, or ADC), converted into a digital signal, and stored as a digital recording.
From a technical standpoint, digital sampling and digital recording are the same thing. A digital representation of sound is a series of discrete numbers that represents the fluctuating voltage of the analog signal. Digital sampling creates a digital representation by taking measurements of instantaneous amplitudes at equally spaced intervals. Each of these equally spaced measurements is a sample. (Be aware that the word "sample" is also used to describe the digital recording in its entirety.) Even though measurements of the fluctuating voltage are not taken at every moment of the analog signal, a large number of samples can quite accurately represent an analog signal in the digital environment.
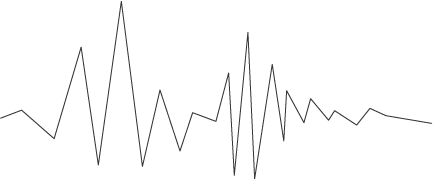
The waveform that results from the analog-to-digital conversion process is not an exact duplicate of the analog waveform, but rather an approximation of the original.
Example 8-2: An A/D converter samples the amplitude of the analog signal, resulting in an approximation of the analog waveform.
There are two aspects to this conversion process, one concerning how often the amplitude is measured, and one having to do with how the measurements of amplitude are recorded.
The rate at which measurements of the amplitude are made is the sampling rate, usually expressed by the number of measurements, or samples, taken per second. Sampling rates of 44,100 per second and 48,000 per second are standard, but other rates, ranging from 6,000 to 96,000, are also common.


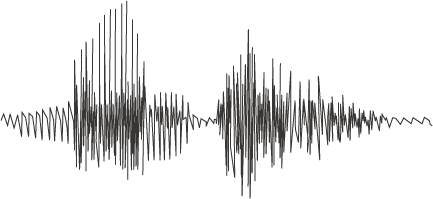
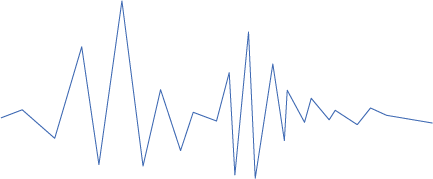
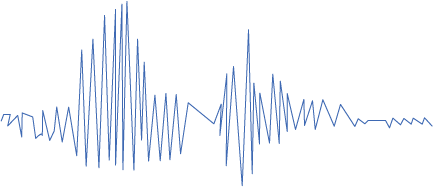
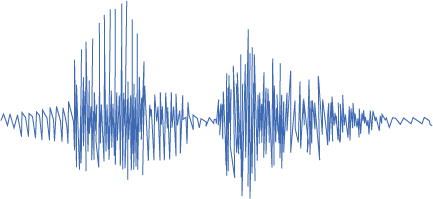

Low Sample Rate
Example 8-3: The sampling rate refers to the number of measurements of amplitude, or samples, taken per second. Here you can hear examples of 4000, 8000, and 22000 samples per second.
To accurately represent the frequency of a waveform a sampling rate must be at least two times the highest frequency contained in the waveform. This minimum sampling rate is called the Nyquist rate; the highest possible sampled frequency given a certain sampling rate is the Nyquist frequency.
Although the waveform that results from sampling is altered from the original, its representation of the frequency remains accurate. Upon playback, a filter will typically follow the conversion process and "round-off" the edges of the sampled waveform, returning it to its original form.
Aliasing is the introduction of false, or alias, frequencies in the digital representation that were not present in the original waveform. If the sampling rate is not at least twice the highest frequency, aliasing will occur.
Example 8-4: The higher the sampling rate, the more accurately the digital waveform can represent the higher frequencies contained in the analog waveform.
The term resolution refers to the number of discrete amplitudes a digital recording (or digital synthesis system) can represent. A digital system cannot record an infinite number of amplitudes. Some systems can represent only several hundred discrete amplitudes, while other systems can represent thousands.
Example 8-5: The measurement of the amplitude must be "rounded-off" to the nearest value that can be recorded.
In some samples the amplitude of the digital representation is between "two points of resolution" and must therefore be moved to the higher or lower point, or value. If the resulting measurement is between two of the possible numbers that can be recorded, then the system must "round-off" the measurement to the nearest recordable value.
Obviously, the less rounding-off, the better the analog signal can be represented in the digital domain. Less rounding-off means more resolution, and a system with more resolution will always produce better sound. The resolution of a system is usually described with terms like "8-bit" or "16-bit". An 8-bit system has 256 values of amplitude and a 16-bit system has 65,536 values of amplitude. Clearly, a 16-bit recording would yield more accurate results.