History of Astronomy:

We have very little in the form of recorded information on early man's impression of the heavens, mostly some drawings of eclipses, comets, supernovae such as the Pueblo Petrograph (see below). However, early man was clearly frightened/overwhelmed by the sky. One of the earliest recorded astronomical observations is the Nebra sky disk from northern Europe dating approximately 1,600 BC. This 30 cm bronze disk depicts the Sun, a lunar crescent and stars (including the Pleiades star cluster).

The disk is probably a religious symbol as well as a crude astronomical instrument or calendar. In the Western hemisphere, similar understanding of basic stellar and planetary behavior was developing. For example, Native American culture around the same time were leaving rock drawings, or petroglyphs, of astronomical phenomenon. The clearest example is found below, a petroglyph which depicts the 1,006 AD supernova that resulted in the Crab Nebula.

Early man also believed that the heavens held power over earthy existence (psychology of the unknown) which is the origins of the pseudo-science astrology as an attempt to understand, predict and influence events

The earliest written records (i.e. history) were astronomical observations produced by the Babylonians (~1600 B.C.) who recorded positions of planets, times of eclipses, etc. There is also evidence of interest in astronomical phenomenon from early Chinese, Central American and North European cultures such as Stonehenge, which is a big computer for calculating the position of planets and the Sun (i.e. when to have that big blowout Solstice thing)

Thus, Astronomy was the 1st science, as it was the first thing we recorded observations for.

Later in history, 5,000 to 20,000 years ago, humankind begins to organize themselves and develop what we now call culture. A greater sense of permanence in your daily existences leads to the development of culture, where people develop narrative stories for cultural unity which we now call myths.

Most myths maintain supernatural themes, with gods, divine and semi-divine figures, but there was usually an internal logical consistence to the narrative. For example, myths are often attempts at a rational explanation off events in the everyday world, their goal is to teach. Even if we consider some of the stories to be ridiculous, they were, in some sense, our first scientific theories. They also, usually, follow a particular religion, and so this time is characterized by a close marriage of science and religion.

Hellenistic Culture (~500 B.C.):

About 1,000 years later, the ancient Greeks inherited astronomical records from the Babylonians and applied the data to construct a cosmological framework. Data was not just used for practical goals, such as navigation, but also to think of new experiments, the origin of what we call natural philosophers.

Of the many natural philosophers before the time of Socrates (the Presocratics) was Thales (~480 B.C.). His combination of math and Babylonian data allowed him to predict eclipses.

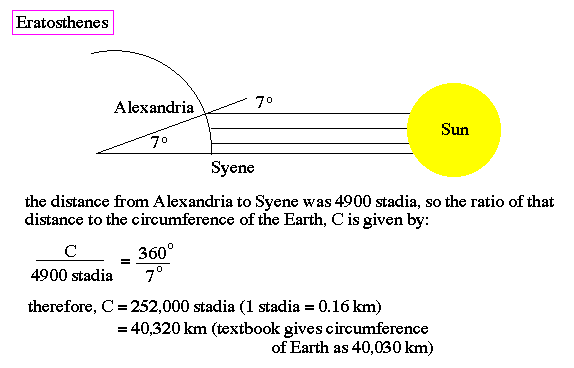
Between the cosmological foundation set by the Presocratics and the world of Ideas introduced by Plato was a set of fundamental calculations on the size of the Earth, Moon, Sun and the distances between the nearby planets performed by Eratosthenes and Aristarchus (c. 250 BC). Using some simple geometry, these two natural philosophers were able to, for the first time, place some estimate of the size of the cosmos in Earth terms.

For a long time it was realized that the earth's surface was curved by people familiar with the behavior of incoming and outgoing ships. For it was obvious that as a ship passed over the horizon, the hull disappeared first, then the topmost sailing masts (although one could argue this is an effect of refraction in the atmosphere). Ancient astronomers could see with their eyes that the Sun and the Moon were round. And the shadow of the Earth, cast on the lunar surface during a lunar eclipse, is curved. A sphere is the simplest shape to explain the Earth's shadow (a disk would sometimes display a shadow shaped like a line or oval).

Eratosthenes used a spherical Earth model, and some simple geometry, to calculate its circumference. Eratosthenes knows that on a special day (the summer solstice) at noon in the Egyptian city of Syene, a stick placed in the ground will cast no shadow (i.e., it is parallel to the Sun's rays). A stick in the ground at Alexandria, to the north, will cast a shadow at an angle of 7 degrees. Eratosthenes realizes that the ratio of a complete circle (360 degrees) to 7 degrees is the same as the ratio of the circumference of the Earth to the distance from Alexandria to Swenet. Centuries of surveying by Egyptian pharaohs scribes gave him the distance between the two cities of 4900 stadia, approximately 784 kilometers. This resulting in a circumference of 40,320 kilometers, which is amazingly close to the modern value of 40,030 kilometers. With this calculation, Eratosthenes becomes the father of geography eventually drawing up the first maps of the known world and determining the size of the most fundamental object in the Universe, our own planet.

Hipparchus (100 B.C.) produced first star catalog and recorded the names of constellations.

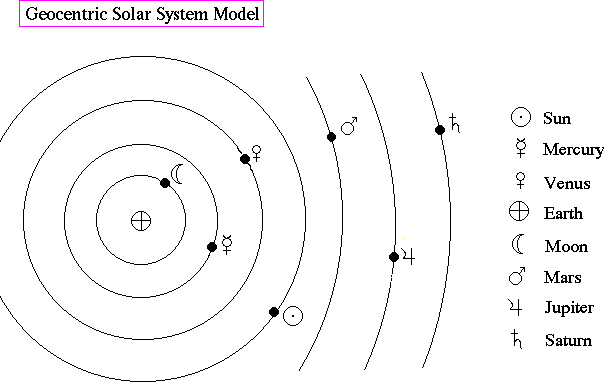
During the times before the invention of the telescope, there were only seven objects visible to the ancients, the Sun and the Moon, plus the five planets, Mercury, Venus, Mars, Jupiter and Saturn. It was obvious that the planets were not on the celestial sphere since the Moon clearly passes in front of the Sun and planets Mercury and Venus can be seen to transit the Sun (the Sun passes in front of Mars, Jupiter and Saturn). Plato first proposed that the planets followed perfect circular orbits around the Earth (for the circle is the most perfect shape). Later, Heraclides (330 B.C.) developed the first Solar System model, placing the planets in order from the Earth it was is now called the geocentric solar system model and the beginning of the geocentric versus heliocentric debate.

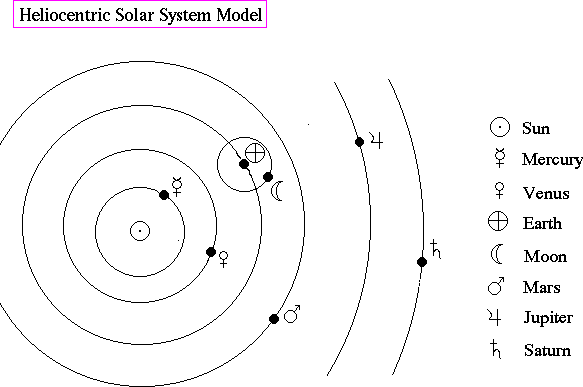
Note that orbits are perfect circles (for philosophical reasons = all things in the Heavens are "perfect")

Slightly later, Aristarchus (270 B.C.) proposed an alternative model of the Solar System placing the Sun at the center with the Earth and the planets in circular orbit around it. The Moon orbits around the Earth. This model became known as the heliocentric model.

Aristarchus was the first to propose a "new" Sun centered cosmology and one of the primary objections to the heliocentric model is that the stars display no parallax (the apparent shift of nearby stars on the sky due to the Earth's motion around the Sun). However, Aristarchus believed that the stars were very distant and, thus, display parallax's that are too small to be seen with the eye (in fact, the first parallax will not by measured until 1838 by Friedrich Bessel). The Sun is like the fixed stars, states Aristarchus, unmoving on a sphere with the Sun at its center. For Aristarchus it was absurd that the "Hearth" of the sky, the Sun, should move and eclipses are easy to explain by the motion of the Moon around the Earth.

Problems for Heliocentric Theory:

While today we know that the Sun is at the center of the solar system, this was not obvious for the technology of the times pre-1500's. In particular, Aristarchus' model was ruled out by the philosophers at the time for three reasons:

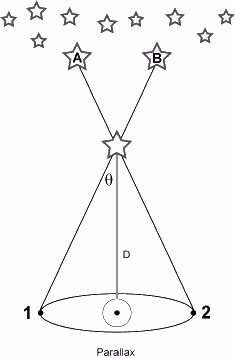
  1. Earth in orbit around Sun means that the Earth is in motion. Before the discovery of Newton's law of motion, it was impossible to imagine motion without being able to `feel' it. Clearly, no motion is detected (although trade winds are due to the Earth's rotation).
  2. If the Earth undergoes a circular orbit, then nearby stars would have a parallax. A parallax is an apparent shift in the position of nearby stars relative to distant stars.

    Of course, if all the stars are implanted on the crystal celestial sphere, then there is no parallax.

  3. Lastly, geocentric ideas seem more `natural' to a philosopher. Earth at the center of the Universe is a very ego-centric idea, and has an aesthetic appeal.
Ptolemy (200 A.D.) was an ancient astronomer, geographer, and mathematician who took the geocentric theory of the solar system and gave it a mathematical foundation (called the "Ptolemaic system"). He did this in order to simultaneously produce a cosmological theory based on Aristotle's physics (circular motion, no voids, geocentric) and one that would provide a technically accurate description of planetary astronomy. Ptolemy's system is one of the first examples of scientists attempting to "save the phenomena", to develop a combination of perfect circles to match the irregular motion of the planets, i.e., using concepts asserted by pure reason that match the observed phenomenon.

Ptolemy wrote a great treatise on the celestial sphere and the motion of the planets call the Almagest. The Almagest is divided into 13 books, each of which deals with certain astronomical concepts pertaining to stars and to objects in the solar system. It was, no doubt, the encyclopedic nature of the work that made the Almagest so useful to later astronomers and that gave the views contained in it so profound an influence. In essence, it is a synthesis of the results obtained by Greek astronomy; it is also the major source of knowledge about the work of Hipparchus, who made a map of the heavens and named the constellations.

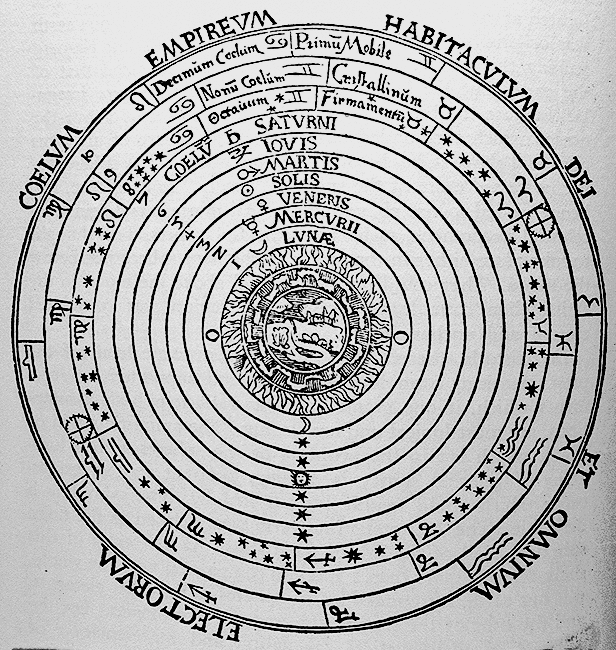
The Christian Aristotelian cosmos, engraving from Peter Apian's Cosmographia, 1524

In the first book of the Almagest, Ptolemy describes his geocentric system and gives various arguments to prove that, in its position at the center of the universe, the Earth must be immovable. Not least, he showed that if the Earth moved, as some earlier philosophers had suggested, then certain phenomena should in consequence be observed. In particular, Ptolemy argued that since all bodies fall to the center of the universe, the Earth must be fixed there at the center, otherwise falling objects would not be seen to drop toward the center of the Earth. Again, if the Earth rotated once every 24 hours, a body thrown vertically upward should not fall back to the same place, as it was seen to do. Ptolemy was able to demonstrate, however, that no contrary observations had ever been obtained.

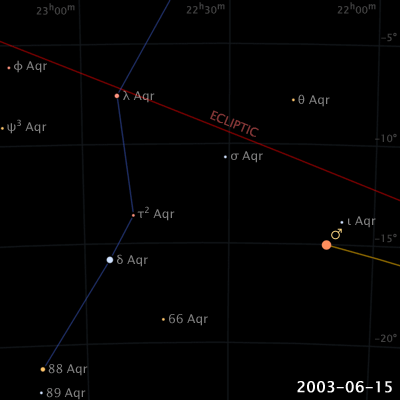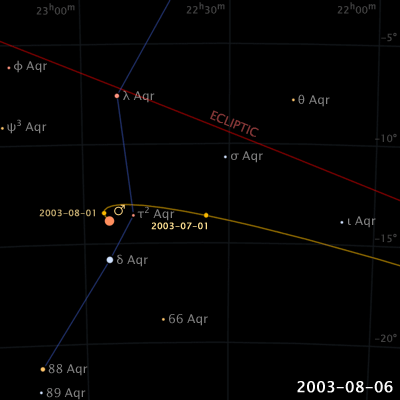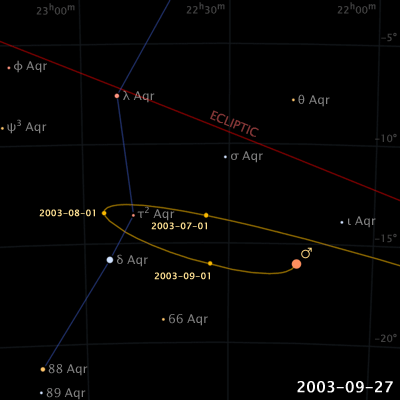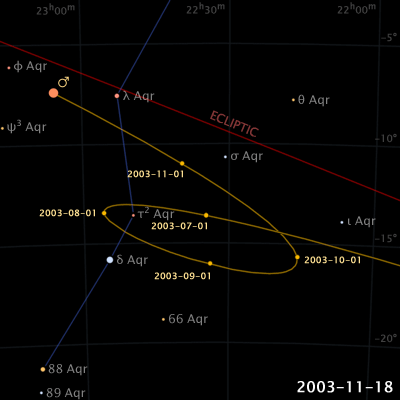
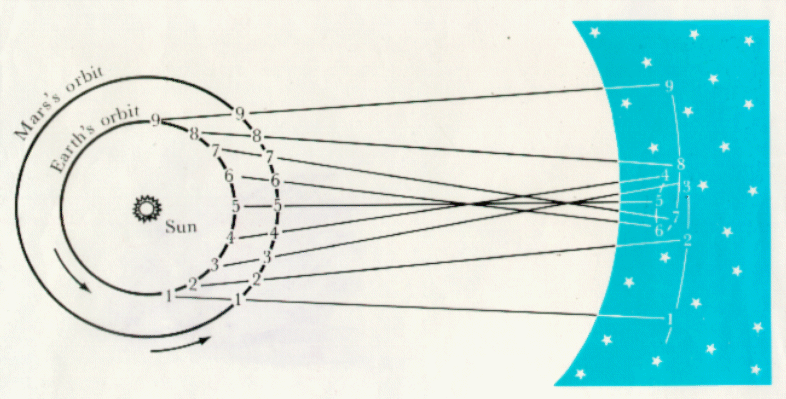
Ptolemy accepted the following order for celestial objects in the solar system: Earth (center), Moon, Mercury, Venus, Sun, Mars, Jupiter, and Saturn. However, when the detailed observations of the planets in the skies is examined, the planets undergo motion which is impossible to explain in the geocentric model, a backward track for the outer planets. This behavior is called retrograde motion.

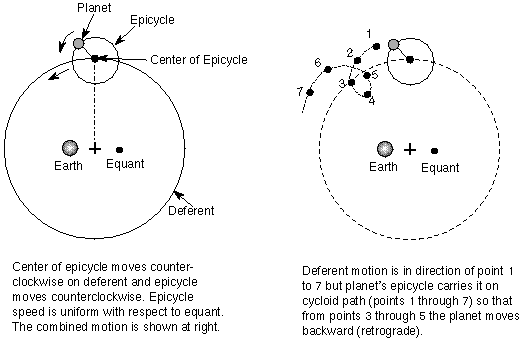
The solution to retrograde motion was to use a system of circles on circles to explain the orbits of the planets called epicycles and deferents. The main orbit is the deferent, the smaller orbit is the epicycle. Although only one epicycle is shown in the figure below, over 28 were required to explain the actual orbits of the planets.

In the Ptolemaic system, deferents were large circles centered on the Earth, and epicycles were small circles whose centers moved around the circumferences of the deferents. The Sun, Moon, and planets moved around the circumference of their own epicycles. In the movable eccentric, there was one circle; this was centered on a point displaced from the Earth, with the planet moving around the circumference. These were mathematically equivalent schemes.

Although Ptolemy realized that the planets were much closer to the Earth than the "fixed" stars, he seems to have believed in the physical existence of crystalline spheres, to which the heavenly bodies were said to be attached. Outside the sphere of the fixed stars, Ptolemy proposed other spheres, ending with the Primum Mobile ("prime mover"), which provided the motive power for the remaining spheres that constituted his conception of the universe. His resulting solar system model looked like the following, although the planets had as many as 28 epicycles (not shown) to account for all the details of their motion.

This model, while complicated, was a complete description of the Solar System that explained, and predicted, the apparent motions of all the planets. The Ptolemic system began the 1st mathematical paradigm or framework for our understanding of Nature.

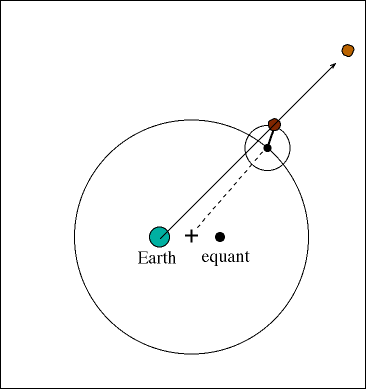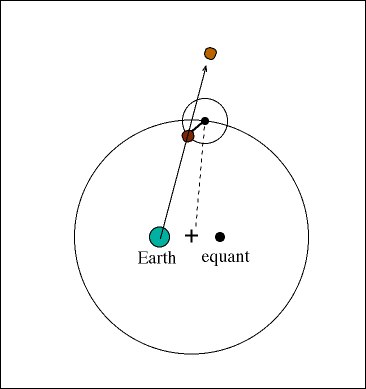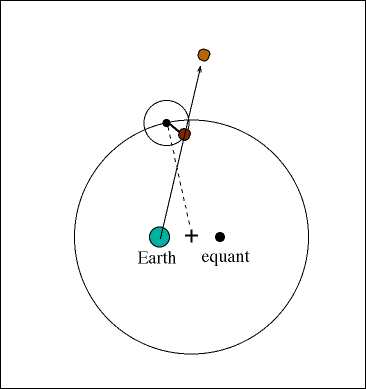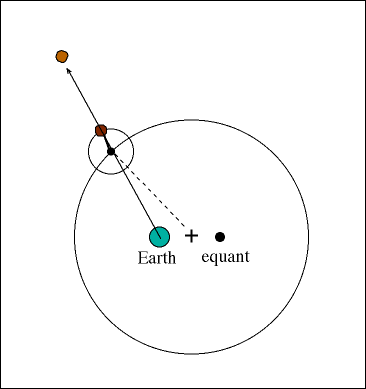
We know from history that the great library at Alexandria burns in 272 AD, destroying a great deal of the astronomical data for the time. Roman culture collapses and we enter the Dark Ages. But, the Roman Catholic Church absorbs Aristotle's scientific methods and Ptolemy's model into its own doctrine. Thus, preserving the scientific method and Ptolemy's Solar System. Unfortunately, the geocentric model was accepted as doctrine and, therefore, was not subjected to the scientific method for hundreds of years.

Until ... the Renaissance, where new ideas were more important than dogma.

Copernicus (1500's) reinvented the heliocentric theory and challenged Church doctrine. Copernicus (c. 1520) was not the first astronomer to challenge the geocentric model of Ptolemy, but he was the first to successfully formulate a heliocentric model and publish his model. He was able to overcome centuries of resistance to the heliocentric model for a series of political and scientific reasons. Politically, the authority of the Church was weakening in Northern Europe in the 15th century allowing more diversity in scientific thinking (although the new Protestant faiths were also not quick to embrace the heliocentric model). Scientifically, a better understanding of motion (particularly inertia) was undermining the whole concept of an unmoving Earth. A rotating Earth is a much simpler explanation for the diurnal motion of stars, an Earth that rotates is only one step away from an Earth that revolves around the Sun. The heliocentric model had a greater impact than simply an improvement to solve retrograde motion. By placing the Sun at the center of the Solar System, Copernicus forced a change in our worldview = paradigm shift or science revolution.

Copernicus began his quest for an improved solar system model with some basic principles. Foremost was the postulate that the Earth was not the center of the Universe, only the center of local gravity and the Moon. Second, the postulate that the Sun was the center of the solar system, all planets revolved around the Sun. In this fashion, retrograde motion is not cause by the planets themselves, but rather by the orbit of the Earth.

While Copernicus includes a rotating Earth in his heliocentric model, he continues to cling to Aristotle's celestial motions, i.e. orbits that are perfect circles (rather than their true shape, an ellipse). This forces Copernicus to adopt a series of moving sphere's for each planet to explain longitude motion. While Copernicus has fewer sphere's, since more of the retrograde motion is accounted for, his system is still extremely complicated in a computational sense. It's two greatest advantages is that it places the inferior planets near the Sun, naturally explaining their lack of large eastern or western elongations, and removing any extreme motions, such as that needed to explain durnal changes.

Copernicus also changes the immovable empyrean heaven into a fixed sphere of stars, severing theology from cosmology. However, Copernicus fails to produce a mechanically simple scheme for astrologers to cast horoscopes or astronomers to produce almanacs, for ultimately the tables he produces are as complicated as Ptolemy's and he did not publish all his results in the final edition of his work, "On the Revolutions of the Heavenly Spheres".

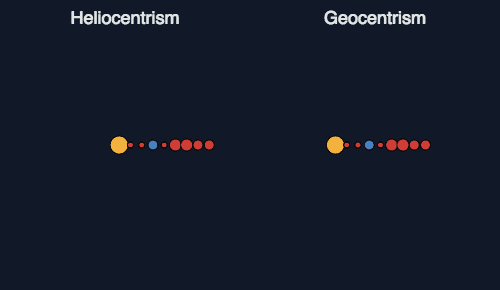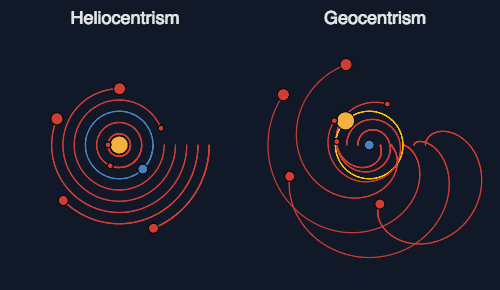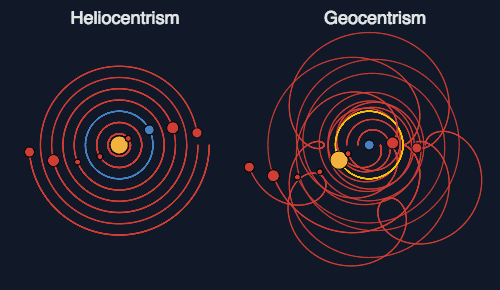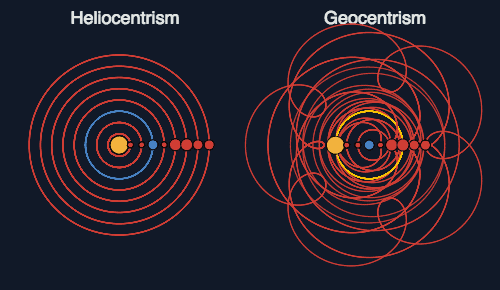
However, Copernicus, like Ptolemy, also used circular orbits and had to resort to epicycles and deferents to explain retrograde motions. In fact, Copernicus was forced to use more epicycles than Ptolemy, i.e. a more complicated system of circles on circles. Thus, Copernicus' model would have failed our modern criteria that a scientific model be as simple as possible (Occam's Razor).

Tycho Brahe (1580's) was astronomy's 1st true observer. He built the Danish Observatory (using sextant's since telescopes had not been invented yet) from which he measured positions of planets and stars to the highest degree of accuracy for that time period (1st modern database). He showed that the Sun was much farther than the Moon from the Earth, using simple trigonometry of the angle between the Moon and the Sun at 1st Quarter.

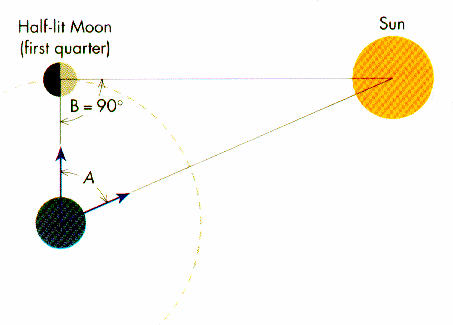
The Earth's motion, as a simple matter of dynamics, was extremely perplexing to the medieval thinker. The size and mass of the Earth was approximately known since Eratosthenes had measured the circumference of the Earth (thus, the volume is known and one could simply multiple the volume with the mean density of rock to obtain a rough mass estimate). The force required to move the Earth seemed impossible to the average medieval natural philosopher.

Brahe had additional reason to question the motion of the Earth, for his excellent stellar positional observations continued to fail to detect any parallax. This lack of annual parallax implied that the celestial sphere was "immeasurably large". Brahe had also attempted to measure the size of stars, not understanding that the apparent size of a star simply reflects the blurring caused by the passage of starlight through the atmosphere. Brahe's estimate for the size of stars would place them larger than the current day estimate of the size of the Earth's orbit. Such "titanic" stars are absurd according to Brahe's understanding of stars at the time.

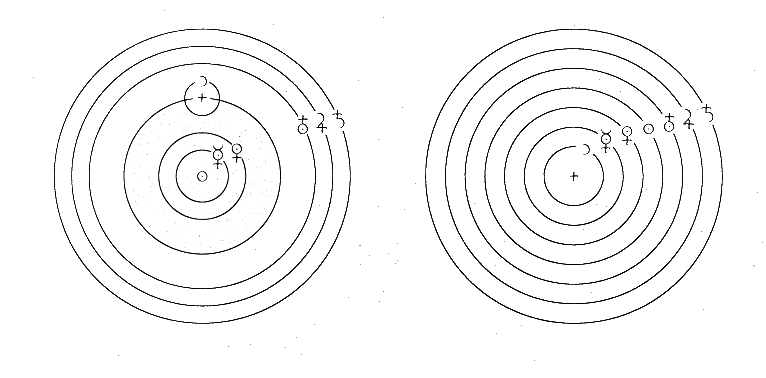
Beyond Tycho Brahe's accomplishments in the observational arena, he is also remembered for introducing two compromise solutions to the solar system model now referred to as the geoheliocentric models. Brahe was strongly influenced by the idea of Mercury and Venus revolving around the Sun to explain the fact that their apparent motion across the sky never takes them more than a few tens of degrees from the Sun (called their greatest elongation). The behavior of inner worlds differs from the orbital behavior of the outer planets, which can be found at any place on the elliptic during their orbital cycle.

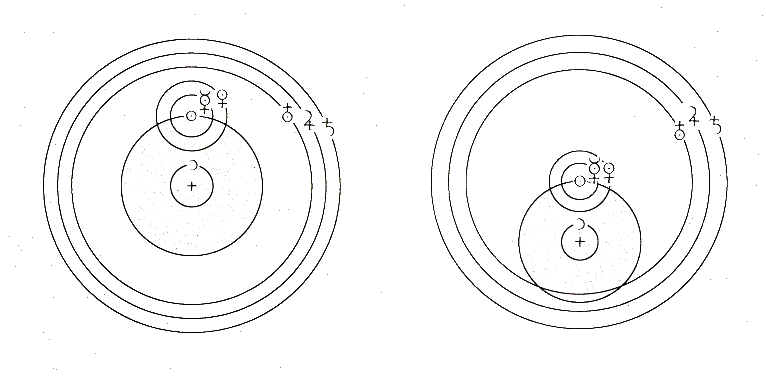
Brahe proposed a hybrid solutions to the geocentric model which preserves the geocentric nature of the Earth at the center of the Universe, but placed the inner planets (Mercury and Venus) in orbit around the Sun. This configuration resolves the problem of Mercury and Venus lack of large angular distances from the Sun, but saves the key criticism of the heliocentric model, that the Earth is in motion. In other works, Brahe's geoheliocentric model fit the available data but followed the philosophical intuition of a non-moving Earth.

Neither successfully predicts the motion of the planets. The solution will be discovered by a student of Tycho's, who finally resolves the heliocentric cosmology with the use of elliptical orbits.

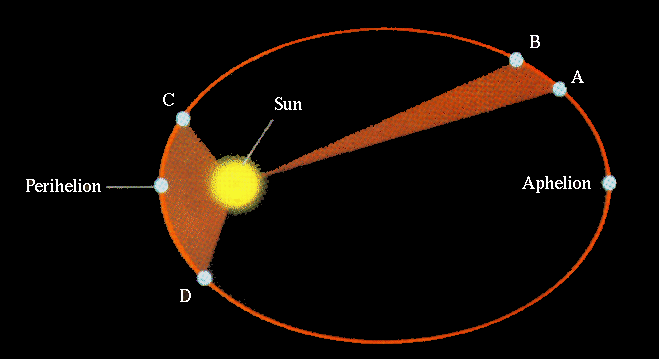
Kepler (1600's) a student of Tycho who used Brahe's database to formulate the Laws of Planetary Motion which corrects the problems of epicycles in the heliocentric theory by using ellipses instead of circles for orbits of the planets.

This is a key mathematical formulation because the reason Copernicus' heliocentric model has to use epicycles is due to the fact that he assumed perfectly circular orbits. With the use of ellipses, the heliocentric model eliminates the need for epicycles and deferents. The orbital motion of a planet is completely described by six elements: the semi-major axis, the eccentricity, the inclination, the longitude of the ascending node, the argument of the perihelion and the time of the perihelion.

The formulation of a highly accurate system of determining the motions of all the planets marks the beginning of the clockwork Universe concept, and another paradigm shift in our philosophy of science.

Galileo:

Kepler's laws are a mathematical formulation of the solar system. But, is the solar system `really' composed of elliptical orbits, or is this just a computational trick and the `real' solar system is geocentric. Of course, the answer to questions of this nature is observation.

The pioneer of astronomical observation in a modern context is Galileo. Galileo (1620's) developed laws of motion (natural versus forced motion, rest versus uniform motion). Then, with a small refracting telescope (3-inches), destroyed the the idea of a "perfect", geocentric Universe with the following 5 discoveries:

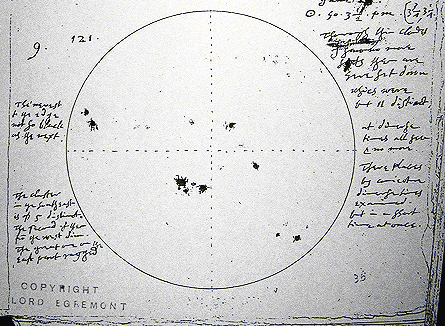
spots on the Sun

mountains and "seas" (maria) on the Moon

Milky Way is made of lots of stars

These first three are more of an aesthetic nature. Plato requires a `perfect' Universe. Spots, craters and a broken Milky Way are all features of imperfection and at odds with Plato's ideas on purely philosophical grounds. However, the laws of motion are as pure as Plato's celestial sphere, but clearly are not easy to apply in the world of friction and air currents etc. So these observations, by themselves, are not fatal to the geocentric theory. The next two are fatal and can only be explained by a heliocentric model.

Venus has phases

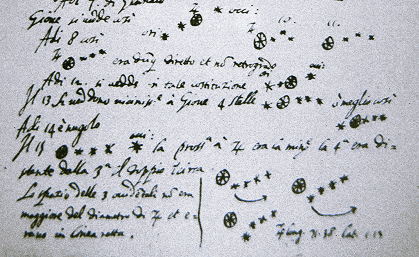
Jupiter has moons (Galilean moons: Io, Europa, Callisto, Ganymede)

Notice that planets with phases are possible in a geocentric model. But for a planet to change in apparent size with its phases, like Venus is impossible if the planet orbits the same distance from the Earth. And, lastly, if all bodies orbit around the Earth, then the moons of Jupiter, which clearly orbit around that planet, are definitive proof that the geocentric model is wrong.

Newton (1680's) developed the law of Universal Gravitation, laws of accelerated motion, invented calculus (math tool), the 1st reflecting telescope and theory of light.

... off to the 18-20th century, with discovery of the outer planets and where astronomy moves towards discoveries in stellar and galactic areas, next paradigm shift occurs in early 1960's with NASA deep space probes

Solar System Right Now