14. Square and Rectangle Waves
The final two common waveforms detailed in Electronic Music Interactive are the square wave and the rectangle wave. As their names might suggest, these two waveforms are related, but square and rectangle waves are also distinct waveforms. The square wave has the following characteristics:
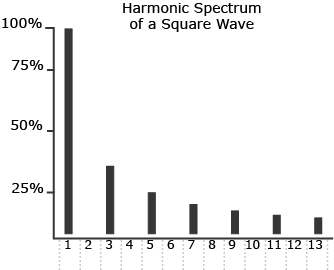
| Frequency Components | Odd Numbered Harmonics |
| Relative Amplitudes of Harmonics | 1/Harmonic Number |
| Phase | All Harmonics in Phase |
In the square wave, every other harmonic is absent. These particular harmonics are missing from the square wave because of its duty cycle. A duty cycle is the percentage of the waveform that occurs above the zero axis. The duty cycle of a square wave is always 50%, or 1/2. Because the duty cycle is 1/2, every second harmonic is not present.
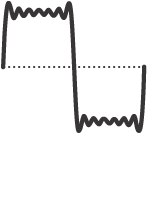
Example 14-1: The building of a square wave, a common waveform.
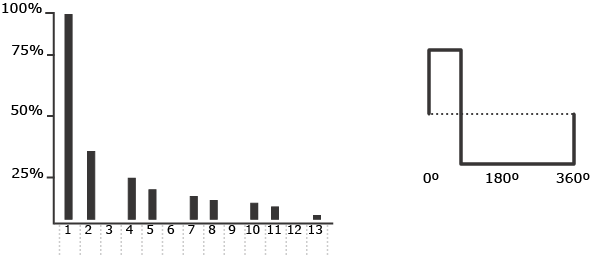
If the duty cycle is any percentage other than 50%, the result is a rectangle wave. The rectangle wave, also called a pulse wave, may have any number of different duty cycles, but like the square wave, its harmonic spectrum is related to its duty cycle. For example, if a rectangle wave has a duty cycle of 25%, or 1/4, every fourth harmonic is missing. If the duty cycle is 20%, or 1/5, every fifth harmonic would be missing. Given a duty cycle of 12.5%, or 1/8, then every eighth harmonic would be missing.
 Waveform
Waveform
Diagram 14-2: Rectangle wave.
The relative amplitudes of the harmonics of both the square and rectangle wave are the same as that of the sawtooth wave. This means that the first harmonic has an amplitude of 1/1, or 1, and that any harmonics after and including the second harmonic will have amplitudes that correspond to their respective harmonic numbers.
By combining sine waves of various frequencies, amplitudes, and phases, a musician can produce a virtually endless number of waveforms. Sound generation of this sort presents a very practical problem, however, because it takes a great amount of time to specify all the components of a waveform.
There is a shortcut, however. The electronic musician can begin the synthesis process with complex waveforms as the starting point, thereby bypassing the time-consuming process of specifying each component frequency.