10. Complex Periodic Waveforms

Fourier Analysis, named after the nineteenth century French mathematician Jean Baptiste Fourier, enables one to break down complex periodic waveforms into their basic components, which happen to be sine waves of various frequencies, amplitudes, and phases. The opposite method, combining sine waves of various frequencies, amplitude, and phase to create complex periodic waveforms, is Fourier Synthesis.

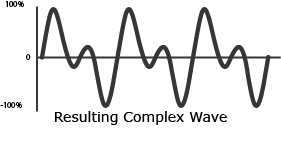
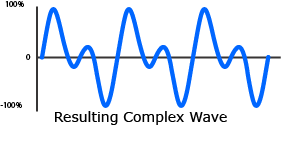
A complex waveform is the result of combining the instantaneous amplitudes of two (or more) sine waves.

Example 10-1: Fourier Synthesis, combining different sine waves, results in complex waveforms.

At some points combined waves reinforce one another to create an increased amplitude, constructive interference, yet at other points combined waves interfere with one another to result in a decreased amplitude, destructive interference.

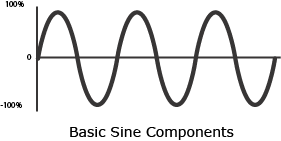
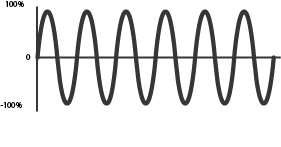
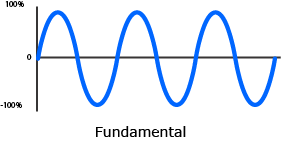
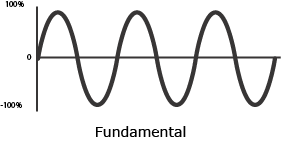
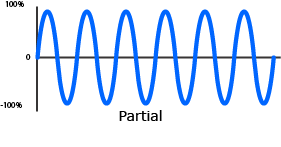
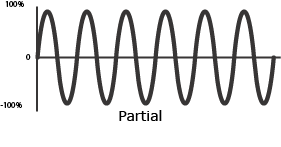
The frequency that has the same period as the resultant waveform is called the fundamental frequency, or fundamental. The fundamental will always be the lowest frequency in a waveform. Frequencies higher than the fundamental are partials.

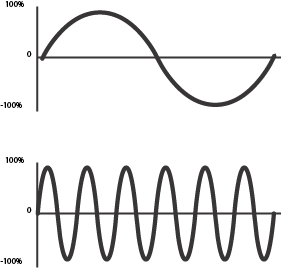Fundamental Partial

Diagram 10-2: Fundamental frequency and partial frequency.