<<Previous

Intro

ch1

ch2

ch3

ch4

ch5

ch6

ch7

ch8

ch9

ch10

Next>>

ch11

ch12

ch13

ch14

ch15

ch16

ch17

ch18

ch19

ch20

ch21

The Observed Properties of Liquid Helium
at the Saturated Vapor Pressure

Chapter 17. Saturated Vapor Pressure

Between 0.65 K and 5.0 K, T90 is defined in terms of the vapor pressure relations of ³He and ⁴He. In this range, the interpolating equation is of the form:


where P is the vapor pressure in Pa. For ⁴He the values of the coefficients Ai and the constants B an C are given in Table 17.1. Although ITS-90 goes onloy down to 0.65 K, this equation is,k in fact, valid to 0.5 K.

Table 17.1. Values of the coefficients in the equation for the saturated vapor pressure for liquid 4He on the T₉₀ scale.

	4He 1.25 K to 2.1768 K	4He 2.1768 K to 5.0 K
A0	1.392408	3.146631
A1	0.527153	1.357655
A2	0.166756	0.413923
A3	0.050988	0.091159
A4	0.026514	0.016349
A5	0.001975	0.001826
A6	-0.017976	-0.004325
A7	0.005409	-0.004973
A8	0.013259	0.0
A9	0.0	0.0
B	5.6	10.3
C	2.9	1.9

Below 1.25 K, the simple equation

suffices to give P in terms of T or vice versa, where L0 = 59.83 J/mol is the latent heat of evaporation at absolute zero, , and R = 8.314510 J/mol•K.

Since the interpolating equation gives temperature as a function of pressure, we offer a spline which returns the pressure as a fuction of temperature. Table 17.2 gives the knots and coefficients.

Table 17.2. Knots and coefficients for the saturated vapor pressure of liquid ⁴He on T₉₀.

Knots	Coefficients	Knots	Coefficients
K(1)=0.5	C(1)=0.00183797	K(18)=1.5	C(18)=1886.00
K(2)=0.5	C(2)=0.00250000	K(19)=1.7	C(19)=3194.00
K(3)=0.5	C(3)=0.00376000	K(20)=1.85	C(20)=5569.50
K(4)=0.5	C(4)=0.00624000	K(21)=2	C(21)=9279.10
K(5)=0.52	C(5)=0.0123600	K(22)=2.2	C(22)=15370.0
K(6)=0.53	C(6)=0.0330600	K(23)=2.5	C(23)=23480.0
K(7)=0.56	C(7)=0.0933900	K(24)=2.7	C(24)=37355.0
K(8)=0.6	C(8)=0.258560	K(25)=3	C(25)=57050.0
K(9)=0.65	C(9)=0.626900	K(26)=3.3	C(26)=87170.0
K(10)=0.7	C(10)=1.37025	K(27)=3.7	C(27)=132825
K(11)=0.75	C(11)=2.93305	K(28)=4.05	C(28)=179650
K(12)=0.8	C(12)=6.37318	K(29)=4.5	C(29)=211567
K(13)=0.85	C(13)=15.0042	K(30)=5.1
K(14)=0.92	C(14)=38.0570	K(31)=5.1
K(15)=1	C(15)=116.050	K(32)=5.1
K(16)=1.1	C(16)=362.700	K(33)=5.1
K(17)=1.25	C(17)=990.900

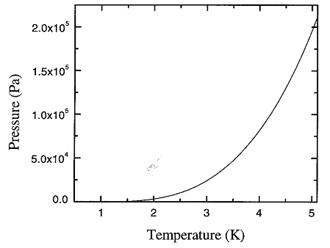
Figure 17.1. The recommended values for the saturated vapor pressure (in Pa) of liquid 4He calculated from the spline

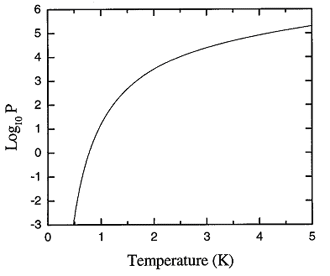
Figure 17.2. Log10 of the saturated vapor pressure curve (in Pa) of liquid 4He.

Table 17.3. Recommended values of the saturated vapor pressure of liquid ⁴He

T90 (K)	P (Pa)	T90 (K)	P (Pa)
0.650	1.101E-01	2.900	2.063E+04
0.700	2.923E-01	2.950	2.229E+04
0.750	6.893E-01	3.000	2.405E+04
0.800	1.475E+00	3.050	2.589E+04
0.850	2.914E+00	3.100	2.783E+04
0.900	5.380E+00	3.150	2.987E+04
0.950	9.381E+00	3.200	3.201E+04
1.000	1.558E+01	3.250	3.425E+04
1.050	2.479E+01	3.300	3.659E+04
1.100	3.802E+01	3.350	3.904E+04
1.150	5.647E+01	3.400	4.160E+04
1.200	8.152E+01	3.450	4.426E+04
1.250	1.147E+02	3.500	4.705E+04
1.300	1.579E+02	3.550	4.994E+04
1.350	2.129E+02	3.600	5.296E+04
1.400	2.819E+02	3.650	5.609E+04
1.450	3.673E+02	3.700	5.935E+04
1.500	4.715E+02	3.750	6.273E+04
1.550	5.971E+02	3.800	6.625E+04
1.600	7.465E+02	3.850	6.989E+04
1.650	9.226E+02	3.900	7.366E+04
1.700	1.128E+03	3.950	7.757E+04
1.750	1.366E+03	4.000	8.162E+04
1.800	1.638E+03	4.050	8.580E+04
1.850	1.949E+03	4.100	9.013E+04
1.900	2.299E+03	4.150	9.461E+04
1.950	2.692E+03	4.200	9.923E+04
2.000	3.130E+03	4.250	1.040E+05
2.050	3.613E+03	4.300	1.089E+05
2.100	4.141E+03	4.350	1.140E+05
2.150	4.716E+03	4.400	1.193E+05
2.200	5.335E+03	4.450	1.247E+05
2.250	6.005E+03	4.500	1.303E+05
2.300	6.730E+03	4.550	1.360E+05
2.350	7.512E+03	4.600	1.419E+05
2.400	8.354E+03	4.650	1.480E+05
2.450	9.258E+03	4.700	1.543E+05
2.500	1.023E+04	4.750	1.608E+05
2.550	1.127E+04	4.800	1.674E+05
2.600	1.237E+04	4.850	1.743E+05
2.650	1.355E+04	4.900	1.813E+05
2.700	1.481E+04	4.950	1.886E+05
2.750	1.614E+04	5.000	1.960E+05
2.800	1.755E+04	5.050	2.037E+05
2.850	1.905E+04	5.100	2.116E+05

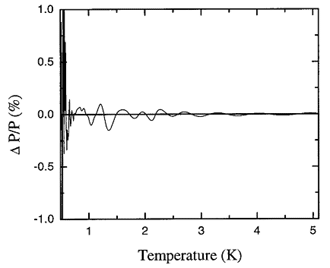
Figure 17.3. The fractional deviation of values of the saturated vapor pressure of 4He calculated with the spline from those calculated with the ITS-90 equations expressed as percent.

It is possible that one might want to know the vapor pressure on the T58 scale since the bulk of available data has been taken on T58. Table 17.4 gives the knots and coefficients of a spline which returns the log10 of the saturated vapor pressure in Hg (the usual unit for T58). Hg = 0.1332 Pa.

Table 17.4. Knots and coefficients of a spline which returns the log10 of the saturated vapor pressure.

Knots	Coefficients
K(1)=1.000000	C(1)=2.079205
K(2)=1.000000	C(2)=2.290418
K(3)=1.000000	C(3)=2.641180
K(4)=1.000000	C(4)=3.067643
K(5)=1.151055	C(5)=3.434872
K(6)=1.287657	C(6)=3.744602
K(7)=1.432021	C(7)=4.016736
K(8)=1.598327	C(8)=4.269063
K(9)=1.740550	C(9)=4.453011
K(10)=1.899594	C(10)=4.558079
K(11)=2.101790	C(11)=4.624146
K(12)=2.176014	C(12)=4.760414
K(13)=2.183220	C(13)=4.923719
K(14)=2.288467	C(14)=5.078931
K(15)=2.579378	C(15)=5.188290
K(16)=2.740483	C(16)=5.287068
K(17)=2.889599	C(17)=5.379486
K(18)=3.040574	C(18)=5.463746
K(19)=3.189656	C(19)=5.543383
K(20)=3.340566	C(20)=5.618267
K(21)=3.479662	C(21)=5.689276
K(22)=3.630567	C(22)=5.756536
K(23)=3.779660	C(23)=5.820032
K(24)=3.920276	C(24)=5.861069
K(25)=4.070000	C(25)=5.880814
K(26)=4.215000
K(27)=4.215000
K(28)=4.215000
K(29)=4.215000

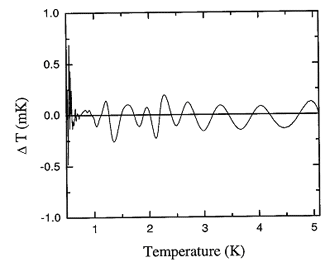
Figure 17.4. Deviations in temperature ?T corresponding to the deviations in pressure shown in Figure 17.3.